Непрерывной называется такая случайная величина, значения которой сплошь заполняют некоторый промежуток.
Непрерывная случайная величина обычно задаётся плотностью распределения f(x).
Свойства плотности распределения:
1) f(x) ³ 0; 2)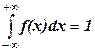 
.
Функция распределения F(x) и плотность распределения f(x) связаны между собой равенствами: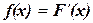 
, 
.
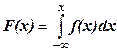Вероятность попадания непрерывной случайной величины на числовой промежуток [ a; b ] выражается через плотность распределения следующим образом: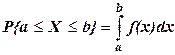 
.
Математическое ожиданиеM[X] непрерывной случайной величины X определяется формулой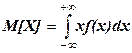 
.
ДисперсияD[X] непрерывной случайной величины X вычисляют по формулам
.
Среднее квадратическое отклонениеs[X] непрерывной случайной величины Х определяется так же, как и для дискретной случайной величины: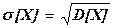 
.
9.1. Непрерывная случайная величина Х подчинена закону распределения с плотностью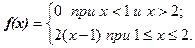 
Найти числовые характеристики M[X], D[X], s[X] данной случайной величины и P { 0 < X < 1,5 }.
9.2. Непрерывная случайная величина Х подчинена закону распределения с плотностью 
Найти коэффициент a, функцию распределения F(x ) и P { X £ 0 }, P { X = –1 }, P { X > 0,5 }.
9.3. Непрерывная случайная величина X имеет функцию распределения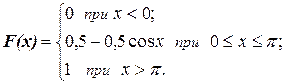 
Найти плотность распределения f(x) и 
. Построить графики функций f(x) и F(x).
9.4. Функция распределения непрерывной случайной величины Х имеет вид F(x) = a + b arctgx. Найти постоянные а и b, плотность распределения f(x) и P { 0 £ X £ 1 }.
9.5. Непрерывная случайная величина Х подчинена закону распределения с плотностью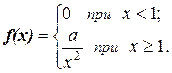 
Найти коэффициент а, функцию распределения F(x) и P { 2 < X < 3 }.
9.6. Непрерывная случайная величина X подчинена закону распределения с плотностью 
Найти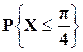 
, 
.
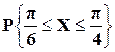9.7. Непрерывная случайная величина Х имеет функцию распределения 
. Найти плотность распределения f(x) и числовые характеристики M[X], D[X], s[X] данной случайной величины.
9.8. Непрерывная случайная величина Х подчинена закону распределения с плотностью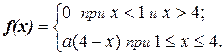 
Найти коэффициент а, функцию распределения F(x) и P { X £ 3 }, P { 2 < X < 5 }, P { X > 3,5 }.
9.9. Непрерывная случайная величина Х имеет функцию распределения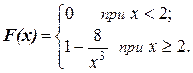 
Найти числовые характеристики M[X], D[X], s[X] данной случайной величины.
9.10. Непрерывная случайная величина Х подчинена закону распределения с плотностью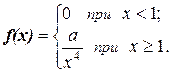 
Найти коэффициент а, функцию распределения F(x) и P { 2 < X < 4 }, P {– 2 £ X < 2 }.
9.11. Скорость молекул газа имеет плотность вероятности (закон Максвелла) 
(
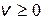). Найти математическое ожидание и дисперсию скорости молекул, а также величину A при заданном h. Указание: 
.
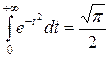