Случайная величина называется дискретной, если все её возможные значения можно перенумеровать.
Дискретная случайная величина обычно задаётся рядом распределения, т.е.
| таблицей вида | х | х1 | х2 | ¼ | хn |
| р | р1 | р2 | ¼ | рn |
Математическое ожиданиеM[X] (или mx ) дискретной случайной величины X вычисляется по формуле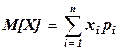 
.
ДисперсияD[X] дискретной случайной величины X определяется формулой
.
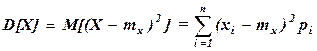Чаще дисперсию удобнее вычислять по формуле
.
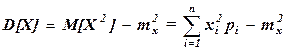Среднее квадратическое отклонениеs[X] случайной величины Х определяется формулой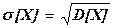 
.
Вероятность попадания дискретной случайной величины на числовой промежуток равна сумме вероятностей значений, попадающих в данный промежуток.
Функция распределения дискретной случайной величины кусочно-постоянная.
8.1. Монету бросают два раза. Случайная величина Х – число выпадений герба. Составить её ряд распределения. Найти M[X], D[X], s[X] и P { X = 0,3 }, P { 0 £ X £ 1,5 }.
8.2. Найти числовые характеристики M[X], D[X], s[X] и P { 1 £ X < 2 }, P { 2 £ X £ 4 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.
| х | |||||
| р | 0,38 | 0,26 | 0,2 | 0,14 | 0,02 |
8.3. Дискретная случайная величина Х принимает три возможных значения: х1 = 4 с вероятностью р1 = 0,5, х2 = 6 с вероятностью р2 = 0,3 и х3 с вероятностью р3. Найти х3 и р3, зная, что M[X] = 8.
8.4. Дан перечень возможных значений дискретной случайной величины Х: х1 = 1, х2 = 2, х3 = 3, а также известны математические ожидания этой величины и её квадрата: M[X] = 2,3, M[X2] = 5,9. Найти вероятности, соответствующие возможным значениям Х.
8.5. Из орудия ведётся стрельба по цели до первого попадания. Вероятность попадания в цель при первом выстреле равна 0,4, при каждом следующем увеличивается на 0,1. Составить закон распределения числа истраченных снарядов, если имеется 4 снаряда. Найти числовые характеристики данной случайной величины.
8.6. Дискретная случайная величина Х принимает три возможных значения: х1 = 1, х2 и х3 , причём х1 < х2 < х3. Вероятности того, что Х примет значения х1 и х2 соответственно равны 0,3 и 0,2. Найти закон распределения величины Х, если M[X] = 2,2, D[X] = 0,76.
8.7. Найти числовые характеристики M[X], D[X], s[X] и P {– 1 < X £ 2 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.
| х | –1 | ||||||||
| р | 0,3 | 0,1 | 0,1 | 0,4 | 0,1 | ||||
8.8. Найти числовые характеристики M[X], D[X], s[X] и P {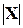 
£ 1 } дискретной случайной величины X, заданной рядом распределения. Построить график функции распределения случайной величины Х.
| х | –2 | –1 | |||
| р | 0,1 | 0,2 | 0,2 | 0,4 | 0,1 |
8.9. Дискретная случайная величина Х принимает два возможных значения: х1 и х2 , причём х1 < х2. Найти закон распределения величины Х, если M[X] = 1,4, D[X] = 0,24, а вероятность того, что Х примет значение х1 равна 0,6.
8.10. Производится ряд выстрелов из орудия с вероятностью попадания 0,8. Стрельба ведётся до первого попадания, но не более 4 выстрелов. Определить примерный расход снарядов на 100 подобных стрельб.
