1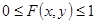 
(Это – свойство вероятности, а 
- вероятность).
2 - неубывающая функция по каждому из своих аргументов. (В самом деле, если 
, то событие 
включено в событие 
, следовательно, его вероятность меньше)
3 
(события 
- невозможные, поэтому их вероятность равна нулю).
4 
(событие 
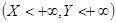достоверно).
5 
= 
- 
- 
+ 
 |
Геометрически, - площадь
полосы левее и ниже точки 
,
Вычитая из нее и ,
мы два раза вычтем площадь
полосы левее и ниже точки 
.
Для того, чтобы получить
площадь прямоугольника –
левую часть равенства, надо
вычитать эту площадь один раз,
поэтому надо добавить ее, т.е.
в правую часть равенства.
6. 
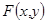непрерывна слева по каждому из аргументов
7. 
. Так как событие 
достоверно, то пересечение событий и 
есть событие . Поэтому первое равенство справедливо. Аналогично доказывается справедливость второго равенства.
Двумерная случайная величина (X,Y) дискретна, если X, Y - дискретные случайные величины. Для нее составляется таблица распределения – аналог ряда распределения для одномерной случайной величины.
| X | Y | ||||
| y1 | y2 | ….. | ym | PX | |
| x1 | p11 | p12 | … | p1m | pX1 |
| x2 | p21 | p22 | … | p2m | pX2 |
| ……. | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnm | pXn |
| PY | pY1 | pY2 | … | pYm |
Здесь pnm = 
, pYm = 
= p1m+ p2m +…+pnm,
pXn = pn1 + pn2 + … +pnm.
График функции распределения для двумерной случайной величины напоминает «лестницу», уровень ступеней которой изменяется скачком на pij при переходе через точку (xi , yj) в положительном направлении по оси OX и по оси OY. Если зафиксировать x = xi, то при увеличении y эти скачки будут на pi1, pi2, … pim (от нуля до pXi). Если зафиксировать y = yj, то при увеличении x скачки будут на p1j, p2j, … pnj (от нуля до pYj). Нижние ступени (при x 
x1 и y y1) находятся на нулевом уровне, самая верхняя ступень (при x>xn, y>ym) находится на уровне 1. Если зафиксировать x > xn то при увеличении y эти скачки будут на pY1, pY2, … pYm (от нуля до 1). Если зафиксировать y > ym, то при увеличении x скачки будут на pX1, pX2, … pXn (от нуля до 1).
Пример. Проводятся два выстрела в мишень. При каждом выстреле вероятность попадания p, вероятность промаха q = 1- p. Случайная величина Xi – число попаданий при i – том выстреле. Найдем закон распределения случайного вектора (X1, X2)= 
.
| X | Y | ||
| y1=0 | y2=1 | PX | |
| x1=0 | q2 | qp | pX1=q |
| x2=1 | pq | p2 | pX2=p |
| PY | pY1=q | pY2=p |
Построим функцию распределения
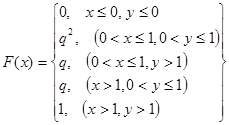. В самом деле, при 
– событие{X<x,Y<y} - невозможное, при (x>1, y>1) событие {X<x,Y<y} – достоверное.
При 
событие {X<x,Y<y} представляет собой событие {X=0,Y=0}. Поэтому при F(x) = P{X=0,Y=0}= q2.
При 
событие {X<x,Y<y} представляет собой объединение несовместных событий {X=0,Y=0} и {X=0,Y=1}. Поэтому при F(x) =. P{X=0,Y=0}+ P{X=0,Y=1}= q2 + pq = q(p+q)=q.Аналогично, в случае 
F(x) = P{X=0,Y=0}+ P{X=1,Y=0}= q2 + pq = q(p+q)=q
Двумерная случайная величина непрерывна, если X, Y, непрерывные случайные величины и ее функцию распределения можно представить в виде сходящегося несобственного интеграла от плотности распределения.
.
Двойной интеграл можно записать в виде повторных (внешний по x, внутренний по y и наоборот). Если предполагать непрерывность плотности по x и y, то, дифференцируя по переменным верхним пределам, получим
.
Свойства плотности.
1. 
(функция распределения – неубывающая функция).
2. 
(по свойству 5 функции распределения) Справедливо обобщение 
.
3. 
4. 
(по свойству 4 функции распределения)
5. 
6. 
, 
(Свойство 7 функции распределения)
