В классическом определении вероятности исходят из того, что пространство элементарных событий Ω содержит конечное число элементарных исходов, причем все они равновозможные.
Случаями называются равновозможные, несовместные события, составляющие полную группу.
В классическом определении вероятности мы находимся в рамках схемы случаев в том смысле, что элементарные события равновозможны, т.е. представляют собой случаи.
Пусть N – общее число случаев в Ω, а NА – число случаев, образующих событие А (или, как говорят, благоприятствующих событию А).
Определение. Вероятностью события А называется отношение числа NA случаев, благоприятствующих событию А к общему числу N случаев, т.е. P(A) =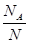 
. Данное определение вероятности события принято называть классическим определением вероятности.
Примеры. 1. Бросание игральной кости. Ω = { w1, w2,…,w 6} N = 6.
А – количество очков кратно трем А = { w3,w6 } NA = 2.
.
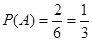2. Бросание 2-х игральных костей. Ω = { w11, w12,…,w66 }; N =36.
wkl = (ak, bl), k,l =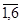 
А – сумма цифр (очков) равна 5. А = {(1,4), (2,3), (3,2), (4,1)}; NA = 4
.
3. В урне а белых и b черных шаров. Опыт – вынимается один шар.
А – шар черный.
Исходя из классического определения вероятностей, легко доказать свойства вероятности:
1) Р(Ω) = 1 (NA = N);
2) 0 
(0 
;
3) Если А В = Ø, то Р(А + В) = Р(А) + Р(В) (NA+B=NA+NB)
и их следствия
4) Р (Ø) = 0 (N Ø) = 0;
5) Р(
) = 1- Р(А) (
= Ø, Р(А) + Р() = 1);
6) Если 
, то Р(А) 
Р(В) (NA NB).
При практическом применении формулы классической вероятности наиболее сложным является определение общего числа равновозможных исходов и числа благоприятствующих исходов.
Здесь используется основной принцип комбинаторики: пусть некоторая операция Р представляет собой последовательность n операций Pk (k=1, …n), каждая из которых может быть выполнена mr способами. Тогда операция Р может быть выполнена 
способами.
Пусть мы делаем выборку поочередно m элементов (например, шаров) из n элементов. Мы можем возвращать очередной шар (в число n шаров), тогда при каждом очередном выборе мы будем иметь все те же n шаров. Такая выборка называется выборкой с возвращением. А можем и не возвращать шар, тогда при каждом выборе мы будем выбирать из все меньшего числа шаров. Такая выборка называется выборкой без возвращения. С другой стороны, мы можем учитывать порядок появления шаров. Такая выборка называется упорядоченной или размещением из n шаров по m шаров. Если порядок шаров при выборе не учитывается, важно лишь, какие шары выбраны, но не важно, в каком порядке, то такая выборка называется неупорядоченной или сочетанием из n шаров по m шаров. Выясним, сколькими способами можнопроизвести ту или иную выборку
| Сочетания | Размещения | |
| Без возвращения |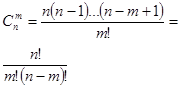 
| 
|
| С возвращением | 
| 
|
Формулы для размещений легко получаются из принципа комбинаторики. Для того, чтобы перейти от размещений (без возвращений) к сочетаниям (без возвращений), нужно упорядочить выборки, т.е. исключить те из них, которые отличаются только порядком элементов. Выборки, отличающиеся только порядком элементов, называются перестановками. Число перестановок из m элементов равно Pm= 
=m!. Поэтому 
.
Формулу для сочетаний с возвращением примем без доказательства (ее доказательство приведено в вып. ХV1 на стр. 50 – 51).
Пример. Производится выборка двух шаров (m=2) из урны, в которой находится 3 шара (n=3). Приведем эти выборки.
1) Размещения с возвращением
(1,1) (1,2) (1,3) (2,1) (2,2) (2,3) (3,1) (3,2) (3,3) 
= 32 = 9.
2) Размещения (без возвращения) (1,2) (1,3) (2,1) (2,3) (3,1) (3,2) 
.
3) Сочетания с возвращением (1,1) (1,2) (1,3) (2,2) (2,3) (3,3) 
4) Сочетания (без возвращения) (1,2) (1,3) (2,3)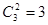 
.
Пример. Задача о выборке бракованных деталей.
В партии из N одинаковых деталей M бракованных. Выбирается (не возвращая) n деталей. Какова вероятность того, что среди них окажется ровно m бракованных?
Общее количество случаев (сочетания из N деталей по n) равно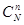 
. Мы выбираем m бракованных деталей среди M бракованных, но и одновременно выбираем (n-m) деталей без брака среди N-M деталей без брака. Тогда, по основному принципу комбинаторики, такому выбору благоприятствует 
случаев. Поэтому искомая вероятность равна 
.
