Формула классической вероятности применяется только в схеме случаев, что встречается довольно редко. Отношение Р(А)= NA/N представляет собой «долю» благоприятных исходов среди всех возможных исходов. Аналогичным образом подсчитывают вероятность события в некоторых более сложных случаях, когда имеется бесконечное число равновозможных исходов.
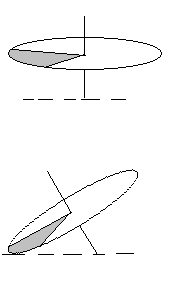
| Событие А – волчок касается плоскости точкой из окрашенного сектора.
Множество точек на ободе в окрашенном секторе имеет мощность континуума. Делим всю окружность на N маленьких одинаковых дуг. Число дуг на окружности, принадлежащих окрашенному сектору, пусть равно NA.
 .
В общем случае имеется мера mes .
В общем случае имеется мера mes 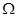 соответствующая соответствующая 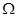 (в нашем случае mes (в нашем случае mes 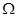 = 2 = 2  ) и мера mes А, соответствующая А (в нашем случае mes А = ) и мера mes А, соответствующая А (в нашем случае mes А =  ) )
 и т.д. и т.д.
|
Пример. Задача о встрече. Два студента договорились встретиться от 10 до 11 часов на определенном месте, причем первый пришедший на место ждет товарища 15 минут и уходит. Какова вероятность встречи?
Выберем начало системы координат в точке (10, 10). Отложим по осям системы координат x- время прихода первого студента, y – время прихода второго студента.
 Тогда множество |x-y|<1/4, 0<x<1, 0<x<1, 0<y<1
Тогда множество |x-y|<1/4, 0<x<1, 0<x<1, 0<y<1
содержит точки (события) встречи студентов. Его мера (площадь) mesA равна 1- (3/4)2 = 7/16. Так как mesW =1, то P(A) = 7/16.
Статистическая вероятность
Формулы классической вероятности и геометрической вероятности справедливы только для случая равновозможных исходов. В действительности мы на практике имеем место с неравновозможными исходами. В этих случаях можно определить вероятность случайного события, используя понятие частоты события. Допустим, что нам требуется определить вероятность того, что в испытании произойдет событие А. Для этого в одинаковых условиях проводятся испытания, в каждом из которых возможны два исхода: А и  . Частотой события А будем называть отношение числа NA испытаний, в которых зафиксировано событие А к общему числу N испытаний.
. Частотой события А будем называть отношение числа NA испытаний, в которых зафиксировано событие А к общему числу N испытаний.
Вероятностью события А называется предел частоты события А при неограниченном увеличении числа испытаний n  , т.е.
, т.е.  . Так определяется статистическая вероятность события.
. Так определяется статистическая вероятность события.
Заметим, что по классическому, геометрическому и статистическому определениям для вероятности события P(A) выполнены три основных свойства:
P(A)³0, 2) P(W)=1, 3) P(A1+ …+An) = P(A1) + …+P(An), если A1, An попарно несовместны. Однако в этих определениях элементарные события предполагаются равновозможными.
А.Н. Колмогоров отказался от предположения равновозможности элементарных событий, ввел сигма-алгебру событий и распространил третье свойство на счетное число событий. Это дало возможность дать аксиоматическое определение вероятности события.
Аксиоматическое определение вероятности (по А.Н.Колмогорову).
Вероятностью P(A) называется числовая функция, заданная на сигма – алгебре событий, удовлетворяющая трем аксиомам:
1) не отрицательность P(A)³0, "AÎB - сигма – алгебре событий на W
2) нормировка P(W) = 1
3) расширенная аксиома сложения: для любых попарно несовместных событий A1, … An … выполнено
P(A1+ …+An+ …) = P(A1) + …+P(An) +…
(счетная аддитивность).
Итак, по А.Н. Колмогорову вероятность (вероятностная мера) это числовая неотрицательная нормированная счетно - аддитивная функция (множества – события), заданная на сигма – алгебре событий.
Если W состоит из конечного или счетного числа событий, то в качестве сигма – алгебры B может рассматриваться алгебра S событий. Тогда по аксиоме 3 вероятность любого события A равна сумме вероятностей элементарных событий, составляющих A.
Вероятностным пространством называется тройка (W, B, P).
Свойства вероятности
1)  . В самом деле,
. В самом деле,  ,
, 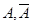 несовместны. По аксиоме 3
несовместны. По аксиоме 3 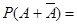
 .
.
2) P(Æ) = 0. Так как "A A+Æ = A, по аксиоме 3 P(A+Æ) = P(A) + P(Æ) = P(A) ÞP(Æ) = 0
3) Если AÌ B, то P(A) £ P(B). Так как B = A+ B\A, по аксиоме 3 P(B) = P(A) + P(B\A), но по аксиоме 1 P(B\A)³0
Пример. Из урны с четырьмя шарами с номерами 1, 2, 3, 4 три раза наугад вынимают шар и записывают его номер а) возвращая шары б) не возвращая шары. Какова вероятность 1) получить комбинацию 111, 2) из номеров шаров составить возрастающую последовательность?
В случае а) имеем размещения с возвращением, N = 43, 1), NA=1, P = ¼3, 2) NA =  , так как возрастающую последовательность можно составить всегда из не повторяющихся номеров, P =
, так как возрастающую последовательность можно составить всегда из не повторяющихся номеров, P =  / 43 .
/ 43 .
В случае б) N =  ,1) P = 0, так как номера шаров не повторяются, то NA =0, 2) P = 1, так как N = NA =
,1) P = 0, так как номера шаров не повторяются, то NA =0, 2) P = 1, так как N = NA =  .
.
Пример. Пять человек садятся в поезд метро, состоящий из пяти вагонов. Какова вероятность того, что они окажутся в разных вагонах?
Общее число элементарных событий равно числу размещений с повторением из пяти элементов по пять N = 55. Число элементарных событий, составляющих А, равно 5! Поэтому Р = 5!/ 55.
Лекция 2
Условная вероятность.
Часто приходится вычислять вероятность события А при дополнительном условии, что произошло событие В. Такую вероятность будем называть условной и обозначать Р(А/В) (вероятность события А при условии, что событие В наступило).
Если никаких дополнительных условий не накладывается, то вероятность называется безусловной. Это – обычная, определенная выше вероятность.
Рассмотрим пример. Пусть в данной аудитории присутствует N студентов. Среди них NA –любящих математику, NB – любящих физику, NАВ – любящих и математику, и физику. Лектор случайно выбирает одного студента. Введем следующие события:
А – случайно выбранный студент любит математику, В – физику, АВ – и математику, и физику. На диаграммах Венна это выглядит так.
 Тогда вероятности этих событий равны:
Тогда вероятности этих событий равны:
 (2.1)
(2.1)
 (2.2)
(2.2)
 (2.3)
(2.3)
Это безусловные вероятности.
Предположим теперь, что мы захотели узнать вероятность того, что случайно выбранный любитель физики любит еще и математику. В этом случае количество всех возможных исходов NB (выбираем только любителей физики), а количество благоприятных исходов – NАВ .
На диаграмме Венна это выглядит так

Тогда, учитывая (2.2) и (2.3), получим
 =
=  =
=  (2.4)
(2.4)
Мы рассмотрели частный случай. Введем в общем случае следующее формальное определение.
Определение. Пусть В – событие, имеющее ненулевую вероятность, а А произвольное событие.
Положим  . (2.5)
. (2.5)
Определенную таким образом величину Р(А/В) будем называть условной вероятностью события А при условии В.






