Формула полной вероятности

Пусть требуется определить вероятность события А, которое может произойти в сочетании с одним из событий Н₁, Н₂,…, Н _n, образующих полную группу несовместных событий ( Ø, ). Эти события будем называть гипотезами.

Н₁ Н₂ Н₃

АН₁ АН₂ АН₃

АН_n-2 АН_n-1 АН_n

H_n-2 H_n-1 H_n

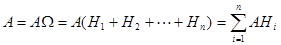
В соответствии со свойством 3) вероятности и теоремой умножения вероятностей

(2.13)

Пример. Из n экзаменационных билетов студент знает m («хорошие билеты» ). Что лучше: брать на экзамене билет первым или вторым?

Решение. Введем событие А – студент взял «хороший» билет.

Студент берет билет первым. В этом случае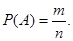

1) Студент берет билет вторым. Введем две гипотезы:

Н₁ – первый студент взял «хороший» билет, Н₂ = .

Вывод: безразлично, брать билет первым или вторым.

 

Формула Байеса (теорема гипотез)

В соответствии с теоремой умножения вероятностей

Р(АН_i) = Р(H_i)·Р(А/H_i) = Р(A)·Р(H_i/А).

В это равенство подставим значение Р(А), вычисленное по формуле полной вероятности (2.13) и найдем Р(H_i/А).

Р(Н_i/A) = (2.14)

Это следствие из теоремы умножения и формулы полной вероятности называется формулой Байеса или теоремой гипотез.

В формуле полной вероятности определяется вероятность события до его появления, т.е. до того, как произведен опыт, в котором оно могло появиться. Вероятности гипотез Р(Н_i), входящие в формулу полной вероятности, называют априорными, т.е. «до опытными».

Пусть опыт произведен и его результат известен, т.е. мы знаем, произошло или не произошло событие А. Получившийся результат мог произойти при осуществлении какой-то одной гипотезы Н_i. Дополнительная информация об исходе опыта перераспределяет вероятности гипотез. Эти перераспределенные вероятности гипотез Р(Н_i/A) называют апостериорными, т.е. «после опытными».

Пример В одной из корзин 1 камешек и 4 кусочка хлеба, во второй – 4 камешка и 1 кусочек хлеба. Мышка наугад выбирает корзину, бежит к ней и вытаскивает кусочек хлеба - событие А (предполагается, что он затем вновь возвращается в корзину). Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине? Какова вероятность того, что она второй раз вытащит кусочек хлеба?

Рассмотрим гипотезы

Н₁ – мышка бежит к первой корзине,

Н₂ – мышка бежит ко второй корзине.

Р(Н₁) =1/2 = Р(Н₂) (априорные вероятности)

.

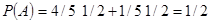
Р(Н₁/A)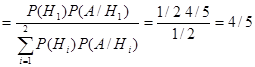

Р(Н₂/A) 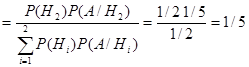(апостериорные вероятности).

При втором подходе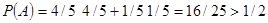

Мышка обучилась, второй раз она выберет первую корзину с большей вероятностью и добьется большего успеха.

Заметим, что это – один из основных принципов обучения кибернетических систем.

 

 

Лекция 3.

 

Случайные величины

 

Случайная величина – это величина (число), которая в результате опыта может принимать то или иное значение.

Более строго, случайная величина – это числовая функция случайного события.

Случайная величина называется дискретной, если множество ее значений конечно или счетно. Здесь 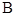- алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.

Случайная величина называется непрерывной, если ее значения заполняют некоторый интервал, возможно, бесконечный. Здесь 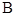- сигма - алгебра событий. Например, расстояние от центра мишени при стрельбе, время до отказа прибора, ошибка измерения – непрерывные случайные величины.

 

Рассмотрим дискретную случайную величину, принимающую значения . Имеем полную группу (иначе, не все значения учтены) несовместных событий 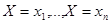. Вероятности этих событий равны соответственно . Будем говорить, что дискретная случайная величина принимает значения с вероятностями .

Законом распределения дискретной случайнойвеличины называется любое соотношение, устанавливающее зависимость между ее значениями и вероятностями , с которыми эти значения достигаются.

Основные формы закона распределения дискретной случайной величины: ряд распределения – таблица

		…..
		…..

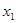
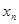
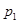
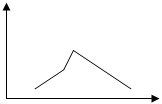
многоугольник распределения

p₃

p₂

p₁, p_n

x₁ x₂ x₃ …x_n

 

Можно задать закон распределения в виде аналитической зависимости, связывающей значения и вероятности .

Рассмотрим непрерывную случайную величину. Для непрерывной случайной величины , поэтому рассматривают события и вероятности этих событий.

Функцией распределения непрерывной случайной величины называется вероятность события . = .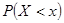