Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: А х = λ х, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А.
Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:
.
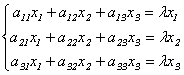Отсюда
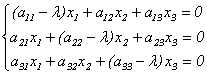. (9.5)
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:
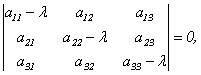
получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:
| A - λE | = 0, (9.6)
поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A - λE | называется характеристическим многочленом матрицы А.
Свойства характеристического многочлена:
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство.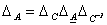 
(см. (9.4)), но 
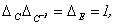следовательно, 
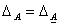. Таким образом, 
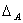не зависит от выбора базиса. Значит, и | A-λE | не изменяется при переходе к новому базису.
2) Если матрица А линейного преобразования является симметрической (т.е. аij=aji), то все корни характеристического уравнения (9.6) – действительные числа.
Свойства собственных чисел и собственных векторов:
1) Если выбрать базис из собственных векторов х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:
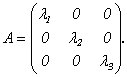(9.7) Доказательство этого свойства следует из определения собственных векторов.
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.
3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.
Пример.
Найдем собственные числа и собственные векторы матрицы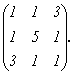 
Составим характеристическое уравнение: 
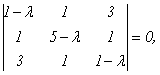(1- λ)(5 - λ)(1 - λ) + 6 - 9(5 - λ) - (1 - λ) - (1 - λ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.
Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х (1) ={ x1,x2,x3 } – собственный вектор, соответствующий λ 1=-2, то
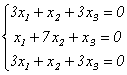- совместная, но неопределенная система. Ее решение можно записать в виде х (1) ={ a,0,- a }, где а – любое число. В частности, если потребовать, чтобы | x (1) |=1, х (1) =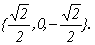 
Подставив в систему (9.5) λ 2=3, получим систему для определения координат второго собственного вектора - x (2) ={ y1,y2,y3 }:
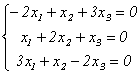, откуда х (2) ={ b,-b,b } или, при условии | x (2) |=1, x (2) =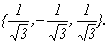 
Для λ 3 = 6 найдем собственный вектор x (3) ={ z1, z2, z3 }:
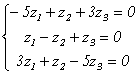, x (3) ={ c, 2c,c } или в нормированном варианте
х (3) =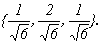 
Можно заметить, что х (1) х (2) = ab – ab = 0, x (1) x (3) = ac – ac = 0, x (2) x (3) = bc - 2 bc + bc = 0. Таким образом, собственные векторы этой матрицы попарно ортогональны.
Лекция 10.
Квадратичные формы и их связь с симметричными матрицами. Свойства собственных векторов и собственных чисел симметричной матрицы. Приведение квадратичной формы к каноническому виду.
Определение 10.1. Квадратичной формой действительных переменных х1, х2,…,хn называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.
Примеры квадратичных форм:
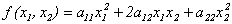(n = 2),
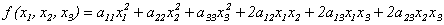(n = 3). (10.1)
Напомним данное в прошлой лекции определение симметрической матрицы:
Определение 10.2. Квадратная матрица называется симметрической, если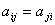 
, то есть если равны элементы матрицы, симметричные относительно главной диагонали.
Свойства собственных чисел и собственных векторов симметрической матрицы:
1) Все собственные числа симметрической матрицы действительные.
Доказательство (для n = 2).
Пусть матрица А имеет вид: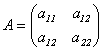 
. Составим характеристическое уравнение:
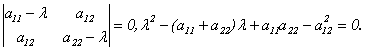(10.2) Найдем дискриминант:
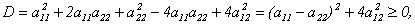следовательно, уравнение имеет только действительные корни.
2) Собственные векторы симметрической матрицы ортогональны.
Доказательство (для n = 2).
Координаты собственных векторов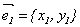 
и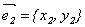 
должны удовлетворять уравнениям:
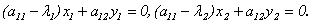Следовательно, их можно задать так:
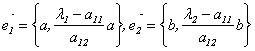. Скалярное произведение этих векторов имеет вид:
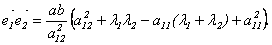По теореме Виета из уравнения (10.2) получим, что 
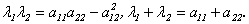Подставим эти соотношения в предыдущее равенство: 
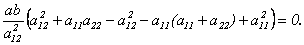Значит, 
.
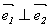Замечание. В примере, рассмотренном в лекции 9, были найдены собственные векторы симметрической матрицы и обращено внимание на то, что они оказались попарно ортогональными.
Определение 10.3. Матрицей квадратичной формы (10.1) называется симметрическая матрица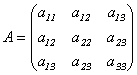 
. (10.3)
Таким образом, все собственные числа матрицы квадратичной формы действительны, а все собственные векторы ортогональны. Если все собственные числа различны, то из трех нормированных собственных векторов матрицы (10.3) можно построить базис в трехмерном пространстве. В этом базисе квадратичная форма будет иметь особый вид, не содержащий произведений переменных.
