Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида
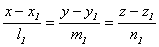и 
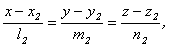косинус угла между ними можно найти по формуле:
. (8.14)
Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:
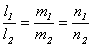- условие параллельности прямых, (8.15)
- условие перпендикулярности прямых. (8.16)
Угол φ между прямой, заданной каноническими уравнениями
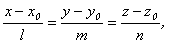и плоскостью, определяемой общим уравнением
Ax + By + Cz + D = 0, можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда
(8.17)
Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:
Al + Bm + Cn = 0, (8.18)
а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m =C/n. (8.19)
Лекция 9.
Линейные преобразования координат. Собственные векторы и собственные числа матрицы, их свойства. Характеристический многочлен матрицы, его свойства.
Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору х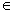 
R по некоторому правилу поставлен в соответствие вектор А х 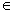R.
Определение 9.1. Преобразование А называется линейным, если для любых векторов х и у и для любого действительного числа λ выполняются равенства:
А( х + у)= А х + А у, А(λ х) = λ А х. (9.1)
Определение 9.2. Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.
Тождественное преобразование обозначается Е: Е х = х.
Рассмотрим трехмерное пространство с базисом е1, е2, е3, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы А е1, А е2, А е3, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:
А е1 = а11 е1 + а21 е2 +а31 е3,
А е2 = а12 е1 + а22 е2 + а32 е3, (9.2)
А е3 = а13 е1 + а23 е2 + а33 е3.
Матрица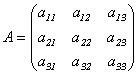 
называется матрицей линейного преобразования А в базисе е1, е2, е3 . Столбцы этой матрицы составлены из коэффициентов в формулах (9.2) преобразования базиса.
Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е.
Для произвольного вектора х =х1 е1 + х2 е2 + х3 е3 результатом применения к нему линейного преобразования А будет вектор А х, который можно разложить по векторам того же базиса: А х =х`1 е1 + х`2 е2 + х`3 е3, где координаты x`i можно найти по формулам:
х`1 = a11x1 + a12x2 + a13x3,
x`2 = a21x1 + a22x2 + a23x3, (9.3)
x`3 = a31x1 + a32x2 + a33x3.
Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.
Преобразование матрицы линейного преобразования
