Найти решение однородной системы:
1. 
2. 
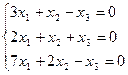
3. 
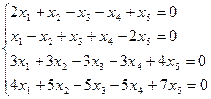
Ответы: 1. XО.Р.= 
, 2. X=(0,0,0)т, 3. XО.Р.=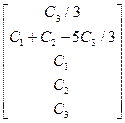 
МОДУЛЬ «ЛИНЕЙНАЯ АЛГЕБРА»
(контрольный блок)
САМОСТОЯТЕЛЬНАЯ РАБОТА
«ДЕЙСТВИЯ С ОПРЕДЕЛИТЕЛЯМИ. ОБРАТНАЯ МАТРИЦА»
Вариант 1.
1. Найти A·C, C·A, B·C, C·B, A·B, B·A, A+B, B+C, C+A, AT, BT, CT, где
A=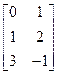 
, B= 
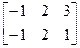, C=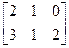 
.
2. Найти определитель:
a)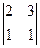 
б) 
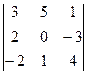в)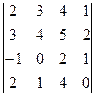 
3. Решить матричное уравнение X·(2·A+E)+B·C=0, где
4. Найти А-1, В-1, где
5. Привести к треугольному виду:
Вариант 2.
1. Найти А∙С, С∙А, В∙С, С∙В, А∙В, В∙А, А+В, В+С, С+А, Ат, Вт, Ст, где
А=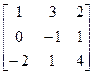 
, В= 
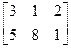, С=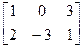 
.
2. Найти определитель:
а) 
б) 
в)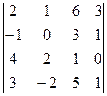 
3. Решить матричное уравнение А∙Х∙В-С=0, где
А= 
, В= 
, С=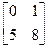 
.
4. Найти А-1,В-1, где
А= 
, В= 
.
5. Привести к треугольному виду:
А= 
В=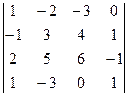 
Вариант 3.
1. Найти А∙С, С∙А, В∙С, С∙В, А∙В, В∙А, А+В, В+С, С+А, Ат, Вт, Ст, где
А=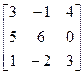 
, В= 
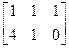, С=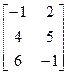 
.
2. Найти определитель:
а) 
б) 
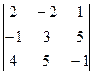в) 
3. Решить матричное уравнение 2∙Х∙А2-В=0, где
А=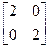 
, В= 
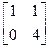, С= 
.
4. Найти А-1,В-1, где
А= 
, В=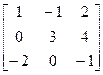 
.
5. Привести к треугольному виду:
А=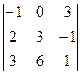 
В=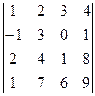 
Вариант 4.
1. Найти А∙С, С∙А, В∙С, С∙В, А∙В, В∙А, А+В, В+С, С+А, Ат, Вт, Ст, где
А= 
, В= 
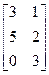, С=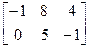 
.
2. Найти определитель:
а)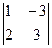 
б) 
в)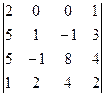 
3. Решить матричное уравнение А∙В∙Х=С+2∙Е, где
А=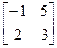 
, В= 
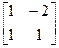, С= 
.
4. Найти А-1,В-1, где
А= 
, В=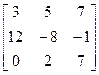 
.
5. Привести к треугольному виду:
А= 
В=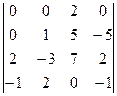 
Вариант 5.
1. Найти А∙С, С∙А, В∙С, С∙В, А∙В, В∙А, А+В, В+С, С+А, Ат, Вт, Ст, где
А=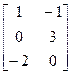 
, В= 
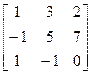, С=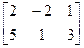 
.
2. Найти определитель:
а)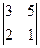 
б) 
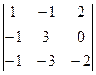в)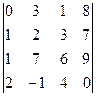 
3. Решить матричное уравнение А∙Х=В+3∙С, где
А= 
, В= 
, С= 
.
4. Найти А-1,В-1, где
А=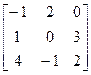 
, В=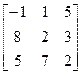 
.
5. Привести к треугольному виду:
А= 
В= 
КОНТРОЛЬНАЯ РАБОТА
“СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ”
Задание:
1.Выполнить действия с матрицами
2.Решить систему уравнений тремя способами (по формулам Крамера, матричным методом, методом Гаусса).
3.Исследовать систему на совместимость и найти решение.
4.Решить однородную систему.
Вариант 1.
1. Найти А2; АВ.
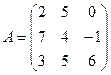
2. 
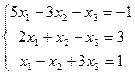
3. 
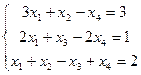4. 
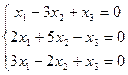
Вариант 2.
1. Найти А2; АВ.
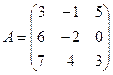
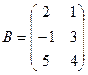
2. 
3. 
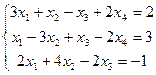4. 
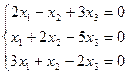
Вариант 3.
1. Найти А2; АВ.
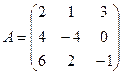
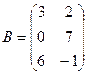
2. 
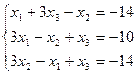
3. 
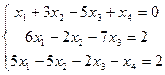4. 
Вариант 4.
1. Найти А2; АВ.
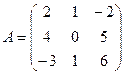
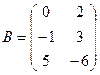
2. 
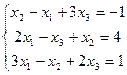
3. 
4. 
Вариант 5.
1. Найти А2; АВ.
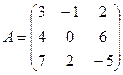
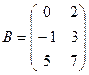
2. 
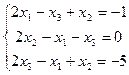
3. 
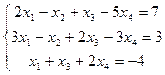4. 
Вариант 6.
1. Найти А2; АВ.
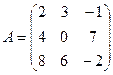
2. 
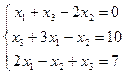
3. 
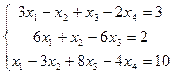4. 
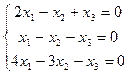
Вариант 7.
1. Найти А2; АВ.
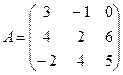
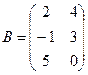
2. 
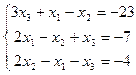
3. 
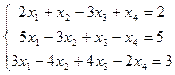4. 
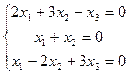
Вариант 8.
1. Найти А2; АВ.
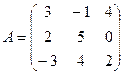
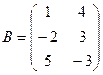
2. 
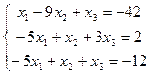
3. 
4. 
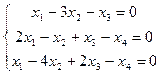
Вариант 9.
1. Найти А2; АВ.
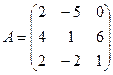
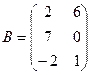
2. 
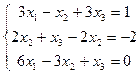
3. 
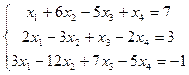4. 
Вариант 10.
1 Найти А2; АВ.
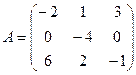
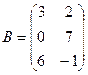
2. 
3. 
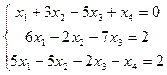4. 
Вариант 11.
1 Найти А2; АВ.
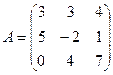
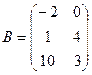
2. 
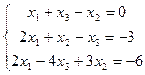
3. 
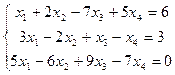4.. 
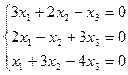
Вариант 12.
1. Найти А2; АВ.
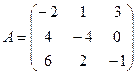
2. 
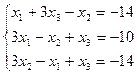
3. 
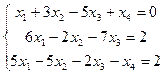4. 
Вариант 13.
1. Найти А2; АВ.
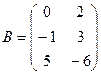
2. 
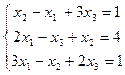
3. 
4. 
Вариант 14.
1. Найти А2; АВ.
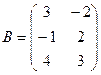
2. 
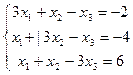
3. 
4. 
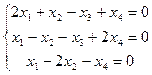
Вариант 15.
1. Найти А2; АВ.
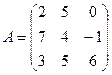
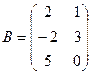
2. 
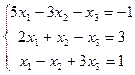
3. 
4. 
Вариант 16.
1. Найти А2; АВ.
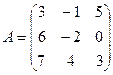
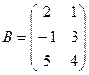
2. 
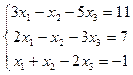
3. 
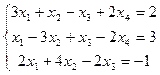4. 
Вариант 17.
1.Найти А2; АВ.
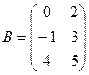
2. 
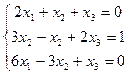
3. 
4. 
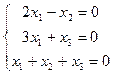
Вариант 18.
1. Найти А2; АВ.
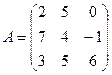
2.
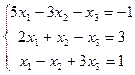
3. 4.
Вариант 19.
1. Найти А2; АВ.
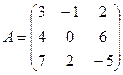
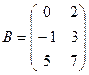
2. 
3. 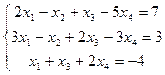4.
Вариант 20.
1. Найти А2; АВ.
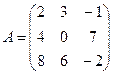
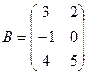
2. 
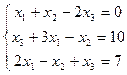
3. 
4.
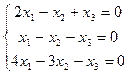
Вариант 21.
1. Найти А2; АВ.
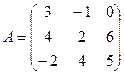
2. 
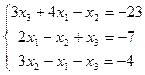
3. 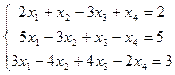4.
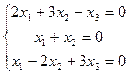
Вариант 22.
1. Найти А2; АВ.
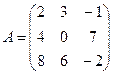
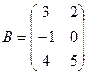
2. 
3. 4.
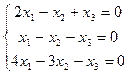
Вариант 23.
1. Найти А2; АВ.
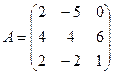
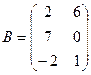
2. 
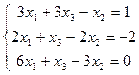
3. 
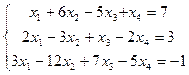4.
Вариант 24.
1. Найти А2; АВ.
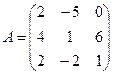
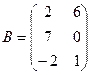
2. 
3. 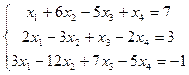4.
Вариант 25.
1. Найти А2; АВ.
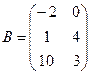
2. 
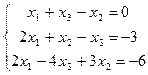
3. 
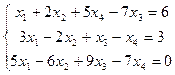4.
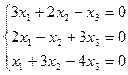
Вариант 26.
1. Найти А2; АВ.
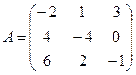
2. 
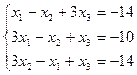
3. 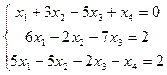4.
Вариант 27.
1. Найти А2; АВ.
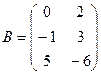
2. 
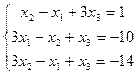
3. 
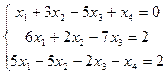4.
Вариант 28.
1 Найти А2; АВ.
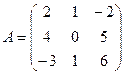
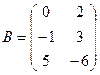
2.
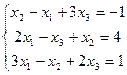
3. 4.
Вариант 29.
1. Найти А2; АВ.
2. 
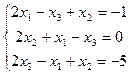
3. 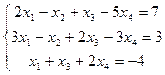4. 
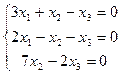
Вариант 30.
1. Найти А2; АВ.
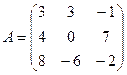
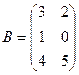
2. 
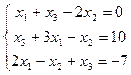
3. 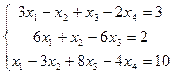4. 
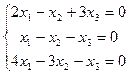
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
1. Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: Учеб. пособие для втузов. В 2-х ч. Ч. l.-4-e изд.-М.: Высш. шк., 1986.-304с.
2. Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов.-14-е изд.-М.: Наука. Гл. ред. физ.-мат. лит., 1986.-224с.
3. Курош А. Г. Курс высшей алгебры: Учебн. пособие для университетов.-10-е изд.- М.: Наука. Гл. ред. физ.-мат. лит., 1971.-432 с.
4. Минорский В. П. Сборник задач по высшей математике: Учеб. пособие для втузов-13-е изд.-М.: Наука. Гл. ред. физ.-мат. лит., 1987.-352с.
5. Сборник задач по курсу высшей математики. Под редакцией П. Е. Дюбюка и Г. И. Кручковича: Учеб. пособие для втузов.-2-е изд -М.: Высш. шк.,1965.-592 с.
6. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов. Под ред. А. В. Ефимова и Б. П. Демидовича.-2-е изд.-М.: Наука. Гл. ред. физ.-мат. лит., 1986.-464 с.
7. Элементы линейной алгебры. Под общ. ред. Р. Ф. Апатенок, М., "Высшая школа", 1977.-256 с.
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
1. Что называется матрицей? Виды матриц. Действия над матрицами.
2. Что называется определителем квадратной матрицы, и каковы его основные свойства?
3. Что называется минором и алгебраическим дополнением элемента?
4. Способы вычисления определителей?
5. Понятие крамеровской системы линейных алгебраических уравнений, ее решение.
6. Какая матрица называется обратной к данной? Как найти обратную матрицу?
7. Как записать простейшее матричное уравнение? Его решение.
8. Что называется рангом матрицы. Как его найти?
9. Что называется матрицей и расширенной матрицей системы?
10. Какая система линейных уравнений называется совместной и несовместной, определенной и неопределенной, однородной и неоднородной?
11. Сформулируйте теорему Кронекера-Капелли. Ее применение для решения произвольных систем.
12. Опишите метод Гаусса.
Теоретические упражнения
(Повышение рейтинга)
1. Пусть A- матрица размера тхп. Какого размера должна быть единичная матрица Е, чтобы имели смысл произведения: А∙Е, Е∙А?
2. Всегда ли можно умножить:
а) строку на столбец;
б) столбец на строку?
Какая матрица получится в результате умножения? Каков ее ранг?
3. Доказать, что определитель треугольной матрицы п-го порядка
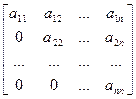
равен а11·а22∙…·ann.
4. Пусть А и В - невырожденные квадратные матрицы порядков т и п соответственно (не исключено, что т=п). Показать, что уравнение А∙Х∙В=С разрешимо только в случае, когда матрица С имеет размер пхт. Записать выражение для матрицы X (в матричном виде), найти ее размер.
