Пусть дана система n линейных уравнений с n неизвестными (т.е. m=n):
(3)
или в матричной форме АХ = В (4)
где А - квадратная матрица порядка n. Определитель матрицы А
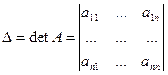называется определителем системы (3) или главным определителем.
Если ∆ ≠ 0, то система (3) называется невырожденной, в противном случае система называется вырожденной.
Для решения невырожденных систем используются формулы Крамера и матричный метод.
Формулы Крамера:
если ∆ ≠ 0, тогда система (3) имеет единственное решение, которое находится по формулам Крамера:
где ∆i - определитель, который получается из определителя ∆ заменой i -го столбца столбцом свободных членов.
Матричный метод:
если ∆ ≠ 0, тогда существует обратная матрица А-1. Решаем матричное уравнение (4): 
.
Так как обратная матрица определяется однозначно, то решение системы (3) будет единственным.
Замечание. Невырожденные с истемы, у которых число уравнений m равно числу неизвестных п, называют системами крамеровского типа или крамеровскими.
Пример.
Найти решение системы уравнений
Данная система является системой крамеровского типа, т.к. содержит m=3 уравнений и n=3 неизвестных.
Находим
Следовательно, существует единственное решение системы, которое найдем по формулам Крамера.
Пример.
Найти решение системы
9
Данная система является системой крамеровского типа, т.к. содержит m=3 уравнений и n=3 неизвестных.
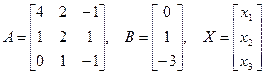
Находим
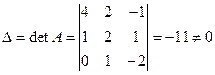
Следовательно, существует единственное решение системы, которое найдем с помощью матричного метода: Х = А-1В.
Задачи для самостоятельного решения.
Решить системы уравнений с помощью формул Крамера или матричным методом:
Метод Гаусса
(метод последовательного исключения неизвестных).
Рассмотрим систему (1). Составим расширенную матрицу системы, разделив элементы матрицы системы и свободные члены вертикальной чертой. Элементы строк, стоящие до вертикальной черты будем называть коэффициентами, а после черты - свободными членами.
Метод Гаусса состоит из двух этапов: прямого и обратного ходов. В процессе прямого хода расширенная матрица системы приводится с помощью элементарных преобразований над строками (перестановка строк, умножение всех элементов некоторой строки на неравное нулю число, вычеркивание одной из пропорциональных строк, прибавление ко всем элементам одной строки соответствующих элементов другой строки, умноженных на некоторое число) к треугольному виду или трапециевидной матрице. В процессе обратного хода составляется равносильная система, из которой легко находятся неизвестные.
Замечание. При решении удобно, чтобы коэффициенты, стоящие на главной диагонали были равны 1. Этого можно достигнуть перестановкой уравнений.
Если в процессе прямого хода получаем:
- в некоторой строке все коэффициенты = 0, а свободный член ≠ 0, то система несовместна, решений нет;
- в некоторой строке все коэффициенты = 0 и свободный член = 0, то эту строку можно вычеркнуть;
- коэффициенты двух строк равны или пропорциональны, а свободные члены соответственно не равны или не пропорциональны, то система несовместна, решений нет;
Проиллюстрируем все сказанное на примере.
Пример.
Найти решение системы
Составим расширенную матрицу и применим прямой ход:
1) переставим первую и вторую строки, чтобы первый элемент первого столбца а11 был равен 1 (для облегчения вычислений);
2) обратим в 0 все элементы первого столбца, стоящие ниже а11: для этого домножаем поочередно первую строку на -2, -1, -5 и прибавляем соответственно ко 2, 3, 4 строке;
3) 2, 3, 4строки являются пропорциональными, следовательно две из них можно вычеркнуть (вычеркиваем 3 и 4):
~ 
~ 
~ 
Следовательно, с помощью элементарных преобразований наша система приведена к виду
Для четырех переменных имеем только две значимых связи, следовательно здесь переменные зависят друг от друга, два неизвестных необходимо объявить свободными. Пусть х3, х4 - свободные неизвестные, тогда
Таким образом, система имеет бесконечное множество решений. Заменим свободные неизвестные х3 =С1, х4 =С2.
Ответ:
Общее решение 
Частное решение (пусть н-р С1 = 0, С2 =1) ХЧ.Р. = (23,-6,0,1)Т.
