Матрицы. Основные определения

 

Матрицей А размера т x п называется прямоугольная таблица чисел или выражений, состоящая из т - строк и n - столбцов. Для обозначения матриц используют следующие записи:

А = ; А = ;

 

Число или выражение, расположенное на пересечении i - ой строки и j - го столбца называется элементом матрицы (a_ij). Если все элементы матрицы -действительные числа, то матрица называется числовой.

Порядком квадратной матрицы называется число ее строк (или столбцов).

Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей. Она имеет вид:

[a₁₁ а₁₂... а_1n]. Пример: [2 9 7 4 5 3].Размер этой матрицы 1х6.

Матрица, состоящая из одного столбца, называется матрицей-столбцом или столбцевой матрицей. Она имеет вид:

Пример: Размер этой матрицы 6х1.

Строки и столбцы матрицы называют ее рядами. Под двумя параллельными рядами понимаются две строки или два столбца матрицы.

Две матрицы А и В называются равными, если они одинаковых размеров и элементы одной матрицы равны соответствующим элементам другой, для всех i и j a_ij=b_ij.

Матрица, у которой число строк равно числу столбцов (m = n), называется квадратной.

Матрицы , , ,

являются квадратными матрицами соответственно первого, второго и третьего порядков.

Элементы а₁₁, а₂₂,..., а_nn составляют главную диагональ, а элементы а_1n, а_2n-1,..., а_n1- побочную диагональ.

 

 

Типы квадратных матриц:

1. Диагональная - матрица, у которой все элементы, стоящие не на главной диагонали, равны нулю, т. е. матрица вида

Пример: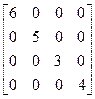

 

 

2. Единичная - диагональная матрица, у которой каждый элемент главной диагонали равен единице, т.е. матрица вида

3. Треугольная - матрица, все элементы которой расположенные по одну сторону от главной диагонали, равны нулю, т.е. матрицы вида

Верхняя треугольная Нижняя треугольная

Пример:

4. Нулевая - матрица, все элементы которой равны нулю, имеет вид

 

Прямоугольная матрица называется трапециевидной, если она имеет вид

Пример:

 

Симметрической называется матрица, элементы которой, симметричные относительно главной диагонали (а₁₁, а₂₂,..., а_nn) равны между собой, то есть для любых i,j=1,2,..., n a_ij=a_{ji .}

 

Операции над матрицами.

Линейные операции над матрицами: сложение матриц, умножение матрицы на число.

Операция сложения возможна только для матриц одинаковых размеров.

Суммой двух матриц А = [а_ij] и В = [b_ij] одинаковой размерности называется матрица С=[c_ij] той же размерности, каждый элемент которой равен сумме соответствующих элементов матриц А и В; т.е. c_ij=a_ij +b_ij.

А + В= + =

Пример:

А = В = А + В =

Произведением матрицы А на действительное число λ называется матрица λ А той же размерности, полученная из А умножением всех ее элементов на число λ:

λ∙А= λ∙ =

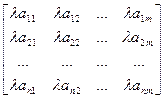
Пример: 1) Произведение матрицы А на число λ = 2 есть матрица

А = 2А =

2) Произведение матрицы В на число λ = 2 есть матрица

В = 2В =

 

Матрица (-1)∙А называется матрица, противоположная матрице А и обозначается -А.

Свойства линейных операций:

1. А+В = В+А( коммутативность).

2. (А + В) +С = А + (В + С) (ассоциативность).

3. А+0 = А.

4. А + (-А)=0.

5. 1·А=А.

6. λ·(μ·А) = (λ·μ)·А ( ассоциативность относительно умножения чисел).

7. λ·(В+А) =λ·А+ λ·В ( дистрибутивность умножения на число относительно сложения матриц).

8. (λ+μ)·А = λ·А+ μ·А( дистрибутивность умножения на матрицу относительно сложения чисел).

(А, В, С, 0 - матрицы одинаковой размерности λ,μ 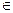R)

Разность матриц А - В определяется следующим образом: А + (-В).

При рассмотрении операции умножения матриц необходимо ввести определение согласованности матриц.

Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Пример: Даны матрицы

А_4x2 = , В_2x4 = , С_3x4= .

Матрица А согласована с матрицей В, так как число столбцов матрицы А равно числу строк матрицы В. Матрица В также согласована с матрицей С, так как число столбцов матрицы А равно числу строк матрицы В. Матрица В также согласована с матрицей С, так как число столбцов матрицы В равно числу строк матрицы С. Матрица А не согласована с матрицей С, так как число столбцов матрицы А равно 2, а число строк матрицы С равно 3. Матрица В не согласована с матрицей А, так как матрица В имеет 3 столбца, а матрица А имеет 4 строки. Матрица С не согласована с матрицей В, так как матрица С имеет 3 столбца, а матрица В имеет 2 строки. Матрица С не согласована с матрицей А, так как матрица С содержит 3 столбца, а матрица А имеет 4 строки.

Если А и В - квадратные матрицы одного порядка, то матрица А согласована с матрицей В и матрица В согласована с матрицей А.

Произведением матрицы А_m×n=(a_ij) на матрицу B_n×k=(b_ij) называется матрица C_m×k=(c_ij) такая, что c_ij= = a_i1b_1j +a_i2b_2j a_i3b_3j +… +a_ipb_pj .

Из определения следует, что элемент матрицы С, находящийся на пересечении i-ой строки и j-го столбца равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.

Замечание. Если матрицу А можно умножить на матрицу В, то отсюда не следует, что матрицу В можно умножить на матрицу А, так как из согласованности матрицы А с матрицей В не следует согласованность матрицы В с матрицей А, то есть в общем случае А ·В ≠·В ·А. Если А·В=В·А, то матрицы называются перестановочными или коммутативными.

Примеры:

1) Найти произведение АВ, если

 

A_3×2= B_2×5= .

Решение: А имеет размеры 3х2, В имеет размеры 2х5, следовательно АВ будет иметь размер 3х5

 

A_3×2·B_2×5= =

= =

 

2) Найти произведения А·В и В·А, если

A= 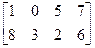, B=

Решение:

A·B= =

B·A= =

Таким образом, результаты умножения матриц А·В и В ·А получились разными, в данном случае А ·В ≠В ·А.

Из определения операции умножения матриц следует, что

А·Е=Е·А=А, А ·0=0·А=0

Свойства операции умножения матриц.

Для матриц А, В, С, 0, Е согласованных размерностей:

1) А·(В+С) = А·В + А·С 4) А·0 = 0

2) (А+В)·С = А·С + В·С 5) 0·В = 0

3) (А·В) ·С = А·(В·С) 6) А·Е = А

7) Е·В = В

Целой положительной степенью Аⁿ (п > 1) квадратной матрицы А называется произведение п матриц, каждая из которых равна А. По определению,

Аⁿ =

Матрица Аⁿ имеет тот же порядок, что и матрица А.

Нулевой степенью А⁰ квадратной матрицы А (А ≠ 0) называется единичная матрица того же порядка,что и А, то есть А⁰ = Е.

Первой степенью А¹ матрицы А называется сама матрица А, то есть А¹ = А.

Произведением степени А^р на степень А^q матрицы А называется сумма степеней А^p+q матрицы А, а именно а^p·а^q = А^p+q ((А^р)^q= А^p·q).

Транспонированием называется операция преобразования матрицы А, заключающаяся в замене строк матрицы столбцами с теми же номерами. Матрица, транспонированная к матрице А обозначается А^´ или А^Т. Таким образом, по определению для матрицы

A = , A^T = .

A= = , где i=1,2,....n; j=1,2,...,m.

Пример: А = , А^Т =

Свойства операции транспонирования:

1) (λ·А)^т =λ·А^Т, λ 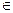R.

2) (А + В)^Т = А^Т + В^Т.

3) (А^Т)^Т = А.

4) (А ∙В)^Т = В^т · а^т.

5) Если А - симметрическая, то А = А^Т.

6) Для любой матрицы А (А^Т·А) и (А·А^Т) всегда симметрические.

7) Если X - n - мерный вектор размера n×1, то

х^T· X = _X1² + Х₂² +... + Х_n², где X =

Задачи для самостоятельного решения.

1. Вычислить линейные комбинации матриц ЗА +2В, если

 

A = B = . Ответ:

 

2. Вычислить А·В-В·А:

А = В = Ответ:

 

3. Вычислить:

3.1 Ответ:

 

3.2 Ответ:

 

4. Найти значение многочлена ƒ (А) от матрицы А:

4.1.ƒ (х)=x²-3·х+1, А = Ответ:

 

4.2. ƒ (х) = Зх²-2х+5, А = Ответ:

 

 

5. Вычислить А∙А^Т и А^Т∙А для заданных матриц А:

5.1. А = Ответ:

5.2. А = Ответ: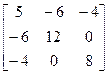

Задание

Согласованы ли матрицы?

Найти произведения: АВ, СА,