1. Не раскрывая определителей, доказать справедливость равенств:
1.1. 
1.2. 
1 Вычислите определитель
1.3. 
1.4 
2. Вычислить определители, используя свойство разложения по строке (столбцу):
2.1. 
2.2. 
2.3. 
2.4. 
3. Вычислите определитель различными способами
3. Используя свойства определителей, решить уравнения и неравенство:
3.1. 
3.2. 
3.3. 
Пример. Вычислить определитель
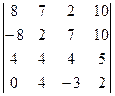
Прежде чем вычислять определитель упростим первый столбец: из первой строки вычтем, а ко второй прибавим удвоенную третью. Полученный определитель разложим по первому столбцу:
Кроме данного способа определитель п- го порядка можно вычислить методом приведения к треугольному виду, то есть с помощью преобразований определителя, когда все его элементы, лежащие по одну сторону от главной диагонали становятся равными нулю. Под преобразованиями определителя понимаются действия умножения строк (столбцов) на число и сложения с другими строками (столбцами).
Пример. Вычислить определитель
Умножим первую строку на (-1) и сложим со второй, третьей и четвертой:
Обратная матрица.
Квадратная матрица А-1 называется обратной для квадратной матрицы А, если А-1·А=А·А-1=Е
Матрица А называется невырожденной (неособенной, обратимой), если для нее существует А-1. Матрица А невырождена тогда и только тогда, когда ∆А ≠ 0
Матрица 
называется союзной или присоединенной к матрице
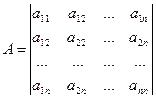
Здесь Аij - алгебраические дополнения к элементам аij матрицы А.
Лемма. Если А - квадратная матрица порядка п, а С - союзная с ней, то A·C=C·A=E·detA.
Теорема 1. Для того, чтобы существовала матрица В, обратная к матрице А, необходимо и достаточно, чтобы матрица А была невырожденной.
Доказательство: Необходимость: пусть существует матрица, обратная к А, тогда А·В=Е и det(A·B)=detA·detB, то есть detA·detB=detE=1. Отсюда следует, что detA ≠ 0, а это и значит, что матрица А невырожденная.
Достаточность: Пусть матрица А невырожденная. Рассмотрим матрицу 
, где С - союзная матрица к А. Согласно лемме A·C=E·detA, разделим это равенство на detA: 
.Аналогично из C·A =E·detA, получаем 
или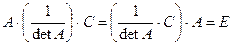 
, тогда по определению обратной матрицы матрица 
является обратной к матрице А.
Теорема 2. Для невырожденной матрицы существует единственная обратная матрица.
Доказательство. Предположим, что для невырожденной матрицы А матрицы 
и 
- обратные. Тогда имеет место равенство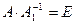 
. Умножим обе части этого равенства слева на : 
или, учитывая, что 
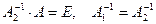. Теорема доказана.
Алгоритм вычисления А,обратной для матрицы А(пхи):
1. Вычислить ∆А (если ∆А ≠ 0, то А-1 существует).
2. Вычислить алгебраические дополнения А ij для всех элементов aij матрицы А сформировать матрицу алгебраических дополнений
3. Транспонировать 
и сформировать союзную (присоединенную) матрицу 
4. Вычислить А-1
.
Свойства обратной матрицы:
1) (А · В) -1 = В-1 ·А-1, если существуют А-1 и В-1
2) (A -1)-1= А.
3) (A Т)-1=(A -1)Т.
4) Е -1 = Е.
5) 
6) Если
Примеры:
1. Найти обратную матрицу А-1, для
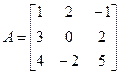
Решение
Найдем определитель матрицы А, det А = -4 ≠ 0. => A-1 существует
Найдем алгебраические дополнения соответствующих элементов матрицы А
Запишем присоединенную матрицу:
Вычислим А-1: 
Пример 3.
Найти матрицу X из уравнения: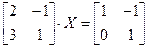 
Решение: обозначим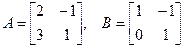 
.
Найдем 
, следовательно матрица А невырожденная. Заданное уравнение имеет вид А·X=В, умножим обе его части слева на А-1, получим: А-1·А ·X=А-1·В, так как А-1·А=Е, то X=А-1·В, таким образом для решения задачи необходимо найти матрицу А-1 и умножить ее на матрицу В.
Пример 4.
Дано матричное уравнение А·Х-2В=С. Найти матрицу X, если известны матрицы 
.
Решение: Выразим матрицу X из уравнения А·Х+С+2В, А-1·А·Х+А-1·(С+2В), так как А-1·А=Е, то Х= А-1·(С+2В).
Найдем С + 2В: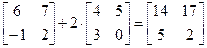 
.
Вычислим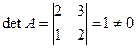 
, следовательно обратная матрица А-1 существует, а именно 
Итак, найдем матрицу
