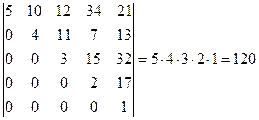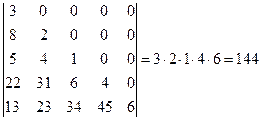Миноры и алгебраические дополнения.
Определителем 2-го порядка квадратной матрицы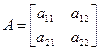 
называется число ∆а (det А, ׀ А ׀ ), которое вычисляется по следующему правилу:
А =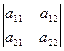 
= a11·a22 – a21·a12,
то есть определитель равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Определителем 3 -го порядка квадратной матрицы А =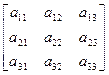 
называется число, вычисленное по следующему правилу
det A =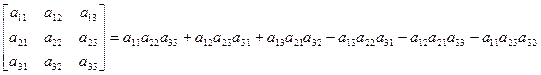 
Данное выражение легко запомнить, если использовать "правило треугольников":
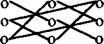
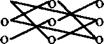
В этой схеме плюс означает, что произведения указанных элементов берутся со своими знаками, а минус - с противоположными.
Определитель 3-го порядка кроме "правила треугольников" можно вычислить по “ правилу параллелограмма”:
- - - + + +,
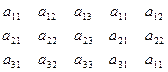
где используется матрица, полученная из пределителя приписыванием справа первых двух столбцов.
Примеры:
1) Вычислить определитель матрицы А по "правилу треугольников":
А =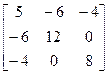 
det A=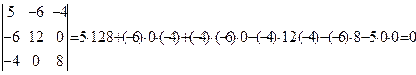 
2) Вычислить определитель матрицы А “ правилу параллелограмма”:
det A= 
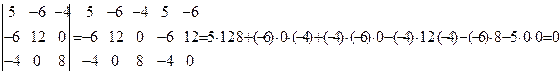
Минором М называется определитель матрицы меньшего порядка, чем исходный, получаемый из него вычеркиванием выбранных произвольно s строк и s столбцов.
Минором М', дополнительным к минору М, называется определитель матрицы, оставшейся после вычеркивания тех s строк и s столбцов данной матрицы, которые входят в минор М.
Минором Мij - элемента аij - называется определитель, полученный из исходного определителя |А| вычеркиванием i - ой строки и j -го столбца на пересечении которых расположен элемент аij..
Алгебраическим дополнением Аij элемента аij называется минор Мij -, взятый со знаком "+", если сумма i+j четная и со знаком "-", если сумма i+j нечетная
Aij=(-1)i+j·Mij.
Пример:
В определителе найти А23, М33:
∆ = 
; A23=(-1)2+3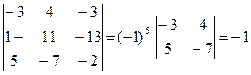 
M33 =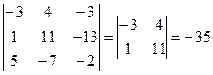 
Задачи для самостоятельного решения.
1. Вычислить определители 2-го порядка:
1.1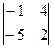 
1.2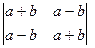 
Ответ:18 Ответ: 4ab
2. Решить уравнение:
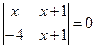Ответ: x1=-1, x2=-4
3. Вычислить определители 3-го порядка:
3.1.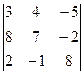 
3.2.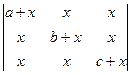 
Ответ: 0 Ответ:. abc+x(ab+bc+ca)
4. Решить уравнение:
Ответ: -4+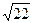 
5. Решить неравенство:
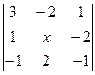‹ 0
Ответ: x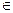 
(4;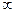 
)
6. Дана матрица
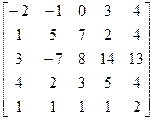
Найти:
1) минор, дополнительный к минору, стоящий на пересечении первой и третьей строк, первого и второго столбцов;
2) алгебраическое дополнение к минору третьего порядка, стоящему в правом верхнем углу;
3) алгебраическое дополнение к минору, стоящему на пересечении первой и второй строк, второго и четвертого столбцов.
Ответ: 1) 30; 2) 2; 3) 13.
7. Дана матрица
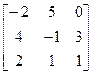
Найти:
1) миноры элементов второй строки;
2) алгебраические дополнения элементов второй строки;
3) алгебраические дополнения элементов третьего столбца.
Ответ: 1) M21=5, M22= -2, M23= -12;
2) A21= -5, A22= -2, A23= 12;
3) A13=6, A23= 12, A33= -18.
Свойства определителей.
1°. Величина определителя не меняется при его транспонировании
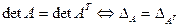
то есть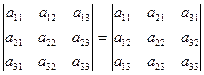 
для определителя 3-го порядка.
2°. При перестановке местами двух рядом стоящих столбцов (строк) определитель меняет свой знак на противоположный,
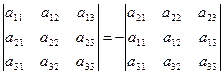
3°. Определитель с двумя одинаковыми столбцами (строками) равен нулю.
4°. Определитель с нулевой строкой (столбцом) равен нулю.
5°. Общий множитель какой-либо строки (столбца) можно выносить за знак определителя,
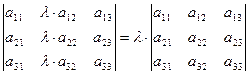
6°. Определитель, в котором соответственные элементы двух столбцов (строк) пропорциональны, равен нулю.
7°. Величина определителя не изменится, если к элементам некоторого столбца (строки) прибавить элементы другого столбца (строки), умноженные на число, не равное нулю.
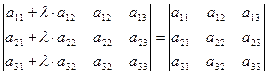
8°. Если каждый элемент n -го столбца (или n -ой строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n -ом столбце (или соответственно в n -ой строке) имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же:
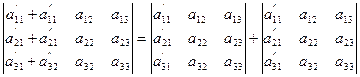
Пример. Вычислить определители, пользуясь их свойствами:
а)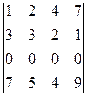 
б) 
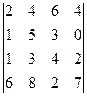в) 
Решение:
а) в определителе третья строка равна нулю, то есть все элементы ее равны нулю, ∆= 0;
б) в определителе пропорциональны первая и третья строки, следовательно (по свойству 6°) он равен нулю;
в) представим определитель в виде суммы двух определителей
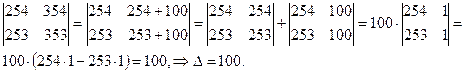
9°. Теорема. Определитель п-го порядка квадратной матрицы А
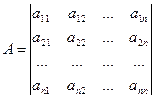
равен сумме произведений элементов любого столбца (строки) на их алгебраические дополнения:
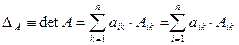
То есть определитель n-го порядка можно свести к вычислению определителей (n-1)-го порядка. Или говорят, что определитель может быть вычислен разложением по любой его i -ой строке или любому k -му столбцу; то есть определитель может быть вычислен разложением по любой его i -ой строке или по любому j -му столбцу.
Например:
-разложение определителя по i-той строке
Представим разложение определителя 3-го порядка по первому столбцу:
Пример. Вычислить определитель
Решение: Величина определителя не изменится, если к первой строке прибавить вторую, умноженную на -2, к третьей строке прибавить вторую, умноженную на 3, к четвертой строке прибавить вторую, умноженную на -4.
Получим: 
Это действие называется “накопление нулей в первом столбце”.
Теперь раскладываем полученный определитель по первому столбцу:
∆=0∙A11+1∙A21+0∙A31+0∙A41 , то есть:
Прибавим к третьей строке вторую:
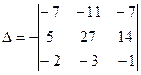
А теперь преобразуем определитель так, чтобы в третьем столбце оказалось два нуля. Для этого к первой строке прибавим третью, умноженную на -7, а ко второй прибавим третью, умноженную на 14. Получим:
Разложим определитель по третьему столбцу:
∆=0∙A13+0∙A23+1∙A33
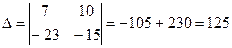
Итак, используя преобразования над строками, мы свели определитель четвертого порядка к определителю второго порядка, формула вычисления которого очень проста.
10°. Если А, В - квадратные матрицы одинаковой размерности, то
det (А·В) = detA ·detB
11°. Определитель диагональной матрицы
Пример:
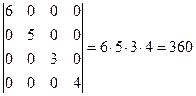
12°. Определитель треугольной матрицы равен произведению элементов главной диагонали:
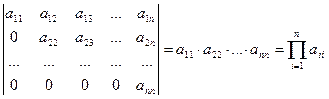
Действительно, легко видеть, что разложив определитель
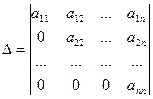
по элементам первого столбца, получим:
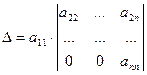
Этот определитель вновь разложим по элементам первого столбца и далее, продолжая данный процесс, получим:
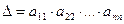
Таким образом, при вычислении определителей иногда удобно предварительно привести его к треугольному виду.
Примеры:
