Исследовать систему на совместность и найти решение в случае совместности

4. Исследовать систему на совместность и найти решение в зависимости от значения параметра λ,

Ответ: 1. XО.Р.=  3. XО.Р.=
3. XО.Р.= 
2. Система несовместна, то есть решений не имеет.
4. При λ≠0 система несовместна; при λ=0 общее решение
XО.Р.= 
Решение однородных систем.
Система уравнений (1) называется однородной, если все bi= 0, i = 1, 2,..., m.
Теорема. Однородная СЛУ всегда совместна (т.е. однородная система всегда имеет хотя бы одно решение - нулевое).
Рассмотрим частные случаи.
1. Если r(А) = n, то существует только нулевое (тривиальное) решение x1=x2=...= xn=0.
2. Если r(А)<n, то существует множество решений (в том числе и нулевое). В этом случае выбирают базисные и свободные неизвестные и затем решают равносильную систему.
3. Система n однородных линейных уравнений с n неизвестными обладает ненулевым решением тогда и только тогда, если определитель этой системы равен 0.
4. Если в системе однородных уравнений m < n, то система непременно обладает решениями, отличными от нулевого.
Кроме общего и частного решений для однородных систем СЛУ выделяют фундаментальную систему решений.
Фундаментальной системой решений (ФСР) системы однородных линейных уравнений называется совокупность максимального числа линейно-независимых вектор-решений.
Если ранг матрицы системы r меньше числа неизвестных n и х1,х2,...,хr -базисные неизвестные, a xn-r, xn-r+1,...,xn - свободные неизвестные, то ФСР состоит и n-r вектор-решений Х1, Х2,...,Хn-r, имеющих следующий вид:
Х1=  , Х2=
, Х2=  , … Хn-r=
, … Хn-r=  .
.
Пример.
Найти решение системы

Данная система является однородной. Число неизвестных n=5>m=4, следовательно, система имеет и ненулевое решение.
Найдем ранг матрицы системы методом элементарных преобразований. Пронумеруем строки и столбцы.
Переставим 1-ю и 4-ю строки;
Домножим поочередно 1-ю строку на -2, -1, -3 и прибавим соответственно ко 2-й, 3-й, 4-й строке;
Я, 3-я, 4-я строки являются пропорциональными, вычеркиваем 3-ю и 4-ю;
Й столбец домножим поочередно на 5, -2, 16, -3 и прибавим соответственно ко 2-му, 3-му, 4-му, 5-му столбцу;
Й столбец домножим поочередно на 7, -25, 4 и прибавим соответственно к 3-му, 4-му, 5-му столбцу;
Вычеркиваем нулевые столбцы;
1 2 3 4 5 1 2 3 4 5
A=  ~
~  ~
~
1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
 ~
~  ~
~ 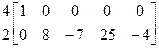 ~
~
1 2 3 4 5 1 2
~  ~
~ 
Итак, r(А) = 2 < n.
Базисные строки - 2,4. Базисные столбцы - 1,2. Базисные неизвестные - х1, х2. Свободные неизвестные - x3, х4, х5.
Приведенная система имеет вид:

Решая приведенную систему, получим:
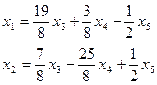
Заменив х3 =С1, х4 =С2, х5 =С3, получим общее решение.
Для записи ФСР берем три линейно-независимых трехмерных вектора (х3,х4,х5): (1,0,0), (0,1,0), (0,0,1). Находим х1 ,х2:
| x3 | x4 | x5 | x1 | x2 |

| 
| |||

| 
| |||

| 
|
Ответ: общее решение ХО.Р. = 
ФСР: X1=  X2=
X2=  X3=
X3= 
Пример.
Найти решение системы

Данная система является однородной n=3,m=4.
A= 
Найдем r(A) методом окаймляющих миноров: r(A)≤n
M2=  M3=
M3= 
Т.к. r(A)=n, то система имеет только нулевое решение.
Ответ: x1=x2=x3=0 или X=(0,0,0)T.




