Рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля или по-другому, рангом матрицы называется максимальное число линейно независимых в ней строк (столбцов). Максимальное число линейно независимых строк и столбцов во всякой матрице одинаково. Ранг матрицы равен нулю, при условии равенства нулю всех миноров матрицы. Обозначение ранга - r или rg.
Две матрицы А и В эквивалентны (А~В), если равны их ранги (r(А) = r(В)).
В матрице А размера т×п минор ∆rпорядка r (r ≤ min {т;п}) называется базисным минором, а его строки и столбцы базисными, если ∆r ≠ 0, а все остальные миноры порядка r+1 равны нулю или не существуют.
Ранг матрицы равен порядку ее базисного минора. Любая строка (столбец) матрицы являются линейной комбинацией ее базисных строк (столбцов). Для квадратной матрицы п- го порядка r=п тогда и только тогда, когда матрица невырожденная.
Свойства ранга матрицы:
1°. Ранг матрицы, полученной из данной вычеркиванием какой-либо строки (столбца) равен рангу данной матрицы или меньше его на единицу.
2°. Ранг матрицы, полученный из данной приписыванием к ней строки (столбца), элементами которой являются произвольные числа, равен рангу исходной матрицы или больше его на единицу.
3°. Если из матрицы вычеркнуть или приписать к ней нулевую строку (столбец), то ранг матрицы не изменится.
4°. Ранг матрицы, полученной из данной транспонированием, равен рангу данной матрицы.
5°. r(A·B)≤min{r(A),r(B)}.
6°. r (А) = r (АT) = r (А T ∙ А) = r (А ∙АT).
7°. Если матрица А - произвольная, а матрицы Р и Q - любые согласованные с матрицей А по умножению квадратные невырожденные матрицы, то r (Р ∙А ∙ Q) = r(А).
Ранг матрицы вычисляется несколькими способами.
Первый способ: с помощью элементарных преобразований. Элементарными преобразованиями называются преобразования следующего вида:
— перестановка местами двух строк (столбцов);
— умножение какой-либо строки или столбца на произвольное число λ≠0;
— прибавление к какой-либо строке (столбцу) линейной комбинации других строк (столбцов).
Теорема. Ранг матрицы, полученной из данной элементарными преобразованиями, равен рангу данной матрицы (или элементарные преобразования не меняют ранга матрицы). Доказательство см. [7], стр. 54-56.
Второй способ: с помощью метода окаймляющих миноров. Минором, окаймляющим минор М порядка k матрицы А, называется минор порядка k+1 этой матрицы, содержащий минор М. Метод окаймляющих миноров состоит в следующем: если в матрице А найдется такой определитель r-го порядка не равный нулю, такой что все определители (r+1)-го порядка, окаймляющие (заключающие) определитель r-го порядка в качестве минора равны нулю, то ранг матрицы А равен r.
Рассмотрим способ вычисления ранга матрицы с помощью элементарных преобразований.
| Пусть дана матрица А, требуется найти r(А). | 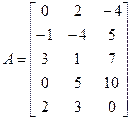
|
| Сначала переставим вторую строку на место первой и умножим ее на (-1), а первую строку на место пятой строки, а пятую строку на место второй строки. | 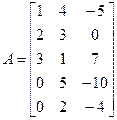 ~ ~
|
| Затем превратим в нули элементы первого столбца, кроме первого, умножив каждый элемент первой строки на (-2) и сложив со второй и умножив на (-3) и сложив с третьей строкой. | ~  ~ ~
|
| Умножим каждый элемент первого столбца на (-4) и прибавим ко второму и также умножим первый столбец на 5 и прибавим к третьему, получим нули в первой строке, кроме первого элемента | ~  ~ ~
|
| Прибавим ко второй строке четвертую, получим нулевую строку, которую вычеркнем, умножим третью строку на (-1/11), а пятую на (-1/12). | ~  ~ ~
|
| Сложим третью и пятую строки, умножим третью строку на 5 и прибавим ко второй, получим две нулевые строки, которые вычеркнем | ~  ~ ~
|
| Умножим каждый элемент второго столбца на 2 и прибавим к третьему, получим нули в третьем столбце | ~  ~ ~
|
| Ранг последней матрицы равен двум, следовательно таков же ранг исходной матрицы, r(А)=2 | ~ 
|
Рассмотрим способ вычисления ранга матрицы методом окаймляющих миноров.
| Пусть дана матрица А Требуется найти r(А). | 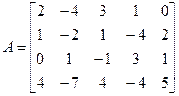
|
Выделим минор 2-го порядка отличный от нуля,  Минор 3-го порядка, окаймляющий минор М2, также не равен нулю
Минор 3-го порядка, окаймляющий минор М2, также не равен нулю 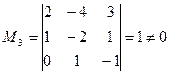
|

|
| Если бы минор 3-го порядка, окаймляющий минор 2-го порядка был равен нулю, то необходимо было бы проверять все миноры 3-го порядка, пока не будет найден хотя бы один нулевой минор. | |
| Теперь найдем миноры 4-го порядка, окаймляющие минор 3-го порядка и проверим их на равенство нулю. Оба минора оказались равными нулю, следовательно наибольший порядок нулевого минора не равного нулю, равен трем, значит и ранг матрицы также равен трем: r(А) =3 | 

|






