


1).Вычислите: 2 
2).Вычислите: sin10°×sin20°×...×sin80 °. [  ]
]
3).Вычислите: tg5°×tg20° + tg20°×tg65° + tg65°×tg5°
Формулы cуммы и разности одноименных тригонометрических функций.


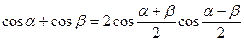



Примеры:
1). sin54° – sin18° = 2sin18°cos36° = 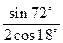 = 0,5
= 0,5
2).  -
- 
3). cos 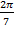 + cos
+ cos 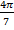 = 2 cos
= 2 cos  cos
cos 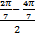 = 2 cos
= 2 cos  cos
cos  = 2 cos
= 2 cos  cos
cos 
4) ctg70° + 4cos70° = 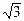 .
.
| Формулы понижения степени и половинного аргумента. |
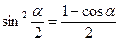


Примеры:
1) Вычислите: sin15°; cos15°; tg15° [  ;
;  ;
;  ].
].
Понятно, что вычислив значения тригонометрических функций для угла 15°, мы знаем и значения тригонометрических функций угла 75°, и, вообще, достаточно вычислять эти значения для углов от 0 до 45°.
Для каких еще углов можно аналогичным образом вычислить значения тригонометрических функций? [22,5°; 37,5°; 7,5° и т. д.]
2) tga =  ; Найти: sin2a (Ответ:
; Найти: sin2a (Ответ: 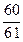 );
);
3).  = 0,6; 0<
= 0,6; 0< 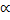 <
<  . Вычислить
. Вычислить  ;
; 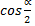 ;
; 
4). Докажите, что в треугольнике АВС один из углов равен 60° т. и т. т., когда sin3A + sin3B + sin3C = 0.
Формулы приведения.
1) Сравните и обоснуйте:
а) 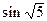 и
и 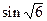 [ >; II четверть];
[ >; II четверть];
б)  и cos(–0,5) [ >; четность; I четверть];
и cos(–0,5) [ >; четность; I четверть];
в) tg1,2p и tg1,4p [ <; показать ось тангенсов ]; г) ctgp2 и ctg10 [ >; показать ось котангенсов ].

|
2) Упростите выражения:
а) sin(1080° – a);
б) cos(–a – 20p);
в) tg(–1800° + b);
г) ctg(14p – b)
ответ: [а) – sina; б) cosa; в) tgb; г) –ctgb]
Помимо свойств четности или нечетности и свойства периодичности тригонометрических функций, существуют правила, позволяющие упрощать аналогичные тригонометрические выражения. Эти правила применяются, когда под знаком тригонометрической функции находятся слагаемые, не кратные 360° или 2p, но кратные 90° или 0,5p. Вывод этих правил, которые называются формулами приведения, использует симметрию на координатной плоскости.
1) Рассмотрим точки Рa и Рp + a. Они симметричны относительно О(0; 0): ZO(Рa) = Рp + a. Следовательно, xp + a = –xa; yp + a = –ya, то есть, cos(p + a) = –cosa; sin(p + a) = –sina; tg(p + a) =  = tga; ctg(p + a) =
= tga; ctg(p + a) =  = ctga.
= ctga.
2) Рассмотрим точки Рa и Рp – a. Они симметричны относительно оси y: S(OY) (Рa) = Рp – a. Следовательно, xp – a = –xa; yp – a = ya, то есть, cos(p – a) = –cosa; sin(p – a) = sina; tg(p – a) =  = –tga; ctg(p – a) =
= –tga; ctg(p – a) =  = –ctga.
= –ctga.
3) Рассмотрим точки Рa и Р0,5p + a. Какова особенность их взаимного расположения? [  ] Следовательно, x0,5p + a = –ya; y0,5p + a = xa, то есть, cos(0,5p + a) = –sina; sin(0,5p + a) = cosa; tg(0,5p + a) =
] Следовательно, x0,5p + a = –ya; y0,5p + a = xa, то есть, cos(0,5p + a) = –sina; sin(0,5p + a) = cosa; tg(0,5p + a) =  = ctga;
= ctga;
ctg(0,5p + a) =  = –tga.
= –tga.
4) Как получить аналогичные формулы для угла 0,5p – a?
[Симметрия относительно прямой y = x или алгебраически]
cos(0,5p – a) = cos(0,5p + (–a)) = –sin(–a) = sina; sin(0,5p – a) = sin(0,5p + (–a)) = cos(–a) = cosa; tg(0,5p – a) = 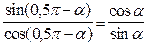 = ctga; ctg(0,5p – a) =
= ctga; ctg(0,5p – a) = 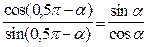 = tga.
= tga.
5) Как получить аналогичные формулы для углов 1,5p ± a? Проще – алгебраически.
cos(1,5p ± a) = cos(p + (0,5p ± a)) = –cos(0,5p ± a) = ±sina; sin(1,5p ± a) = sin(p + (0,5p ± a)) = –sin(0,5p ± a) = –cosa; tg(1,5p ± a) =  = mctga; ctg(1,5p ± a) =
= mctga; ctg(1,5p ± a) = 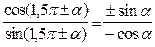 = mtga.
= mtga.
Некоторые формулы приведения:

| 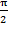 + + 
| π + 
|  + + 
| 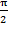 - - 
| π - 
|  - - 
| 2π - 
|

| 
| - 
| - 
| 
| 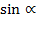
| - 
| - 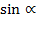
|

| - 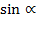
| - 
| 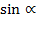
| 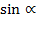
| - 
| - 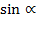
| 
|

| - 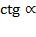
| 
| - 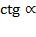
| 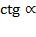
| - 
| 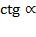
| - 
|

| - 
| 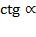
| - 
| 
| - 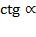
| 
| - 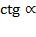
|
Самое замечательное, что сами формулы запоминать не надо, достаточно запомнить «мнемоническое правило».
1) Знак результата совпадает со знаком данной функции;
2) Если есть  или
или  , то название функции меняется на кофункцию;
, то название функции меняется на кофункцию;
3) Если есть π или 2π, то название функции не меняется;
Упражнения.
1) Упростите выражения:
а) sin(117p – a);
б) cos(– 221,5p–a);
в) tg( + b);
+ b);
г) ctg2(b – 1890°) ответ:[а) sina; б) –sina; в) –ctgb; г) tg2b]
2) Вычислите значение тригонометрических функций угла 330°.
[cos330° =  ; sin330° = –0,5; tg330° =
; sin330° = –0,5; tg330° = 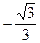 ; ctg330° =
; ctg330° =  ]
]
3) Приведите к значению тригонометрической функции угла, лежащего в промежутке от 0 до 45° (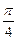 ): а) sin(–3725°); б)
): а) sin(–3725°); б)  [а) –cos39°; б) –ctg
[а) –cos39°; б) –ctg  ]
]
4) Приведите к значению тригонометрической функции угла, лежащего в промежутке от 0 до 45°
а) cos(–2281°); б) ctg27,7p.
5) Определите знаки чисел и попарно сравните: а)  и
и 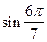 ; б) cos(–2) и cos(–3); в)
; б) cos(–2) и cos(–3); в) 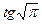 и
и 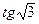 .
.
6) Верны ли равенства (обоснуйте): а) sin(a + b) = sina + sinb; б) cos(a – b) = cosa – cosb? [ Нет; примеры!]
7) Сравните: sin(cos1) и cos(sin1).
8) Вычислите:  [ –1 ];
[ –1 ];
9) Приведите к значению тригонометрической функции угла, лежащего в промежутке от 0 до 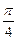 : а) cos10; б) ctg11. [а) –cos(10 – 3p); б) –tg(11 – 3,5p)];
: а) cos10; б) ctg11. [а) –cos(10 – 3p); б) –tg(11 – 3,5p)];
10) Найдите значение выражения: sina×sinb×...×siny×sinz [ 0, так как sinp = 0].
11) Упростите: а) sin8; б) tg(–7).
12)  ·
·  )
)






