Знаменатели дробей разложить на множители.
Найти наименьший общий знаменатель для дробей.
Привести все дроби к найденному знаменателю. Для этого находим дополнительные множители.
Сложить или вычесть дроби по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Пример:
1. Вычислить: – 3,25:  + 6,75 ·
+ 6,75 · 
Решение. Указанные действия надо выполнить, не пользуясь микрокалькулятором, не делая округлений и приближенных вычислений, так как предполагается, что все заданные числа являются точными.
Будем выполнять вычисления по действиям:
1. – 3,25:  = – 3
= – 3  :
:  =
=  :
:  =
=  =
= 
2. 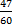 - 2
- 2  - 1,65 =
- 1,65 = 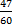 -
-  -
-  =
= 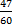 -
-  -
-  =
=  =
=  =
=  =
= 
3. 6,75 ·( ) =
) =  ·
· 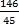 ==
==  = - 21,9
= - 21,9
4.  - 21,9 =0,625 – 21,9 = - 20, 275
- 21,9 =0,625 – 21,9 = - 20, 275
Таким образом, – 3,25:  + 6,75 ·
+ 6,75 ·  =- 20, 275
=- 20, 275
2.  +
+ 
 =
=  ;
;  =
= 
Наименьший общий знаменатель a( )(
)( )
)
 =
=  =
=  ;
;  =
=  =
= 
 +
+  =
=  =
= 
Решить самостоятельно следующие примеры:
1.Привести к общему знаменателю: a)  +
+  b)
b)  -
-  c)
c)  +
+  d)
d) 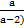 +
+  e)
e)  -
- 
2. Докажите тождество
.  -
-  +
+ 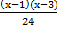 = 1
= 1
3. Зная, что  = 10, найдите значение дроби:
= 10, найдите значение дроби:
а)  ; б)
; б)  ; в)
; в)  ;
;
4. При каком значении переменной b выражение 3 +  тождественно равно дроби
тождественно равно дроби  ?
?
5. Вычислить: - 3 
 (-2
(-2  5,5 + 4,3
5,5 + 4,3  3,7) - 2
3,7) - 2 
(2,8:(2  · (8,75-2
· (8,75-2  ))) · 7,25 - 3
))) · 7,25 - 3  : ((1,2 + 5
: ((1,2 + 5  ) · 3,75)
) · 3,75)
3  :((1
:((1  +2,5) · 3,2)+(4,25: (4
+2,5) · 3,2)+(4,25: (4  · (5,25 - 1
· (5,25 - 1  ))) · 2
))) · 2
Самостоятельная работа№2
Тема 1.2. Разложение многочлена на множители.
Самостоятельная работа№2 (4 часа)
Цель: отработать навык решения квадратных уравнений, разложения многочленов на множители.
План работы:
1. Повторить виды квадратных уравнений и способы их решения.
2. Способы разложения на множители:
вынесение за скобку общего множителя;
группировка.
3. Формулы сокращённого умножения.
Теоретические сведения.
Ключевые слова: множители, разложение на множители, вынесение общего множителя, формулы сокращенного умножения, способ группировки, метод выделения полного квадрата.
Определение. Тождественное преобразование, приводящее к произведению нескольких мн разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.
Вынесение общего множителя за скобки. Этопреобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)
Пример. Разложить многочлен на множители 12 y 3 – 20 y 2.
Решение. Имеем: 12 y 3 – 20 y 2 = 4 y 2 · 3 y – 4 y 2 · 5 = 4 y 2 (3 y – 5). Ответ. 4 y 2(3 y – 5).
Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.
Пример. Разложить на множители многочлен x 4 – 1. Решение. Имеем: x 4 – 1 = (x 2) 2 – 1 2 = (x 2 – 1)(x 2 + 1) = (x 2 – 1 2)(x 2 + 1) = (x + 1)(x – 1)(x 2 + 1). Ответ. (x + 1)(x – 1)(x 2 + 1).
Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.
Пример. Разложить на множители многочлен x 3 – 3 x 2 y – 4 xy + 12 y 2.
Решение. Сгруппируем слагаемые следующим образом:
x 3 – 3 x 2 y – 4 xy + 12 y 2 = (x 3 – 3 x 2 y) – (4 xy – 12 y 2). В первой группе вынесем за скобку общий множитель x 2, а во второй − 4 y. Получаем:
(x 3 – 3 x 2 y) – (4 xy – 12 y 2) = x 2 (x – 3 y) – 4 y (x – 3 y). Теперь общий множитель (x – 3 y) также можно вынести за скобки:
x 2 (x – 3 y) – 4 y (x – 3 y) = (x – 3 y)(x 2 – 4 y). Ответ. (x – 3 y)(x 2 – 4 y).






