Прочитайте выражения: a3 – 53 (2b + 3)3 (2x)3 + 1 (3y2)3 – x3 (9x - y) 3 103 + (5a) 3
Повторить формулы разности и суммы кубов:
a3 – b3 = (a-b)(a2 + ab + b2)
a3 + b3 = (a+b)(a2 - ab + b2)
Повторить формулы сокращенного умножения: разность квадратов, квадрат разности, квадрат суммы.
а2 – b2 = (a-b)(a + b)
(a+b)2 =a2 +2 ab + b2
(a-b)2 =a2 -2 ab + b2
На практике при решении примеров часто приходится использовать комбинацию различных приемов.
Пример 1. 36 a6 b3 – 96a4 b4 + 64a2b5
Решение: 36 a6 b3 – 96a4 b4 + 64a2b5 = 4a2b3(9a4 – 24a2 b + 16b2) = 4a2b3(3a2 – 4b)2.
Комбинировали два приема:
– вынесение общего множители за скобки;
– использование формул сокращенного умножения.
Пример 2. a2 + 2a b + b2 – c2
Решение: a2 + 2a b + b2 – c2 = (a2 + 2a b + b2) – c2 = (a + b)2 – c2= (a + b – c) (a + b + c)
Комбинировали два приема:
– группировку;
– использование формул сокращенного умножения.
Пример 3. y3 – 3y2 + 6y – 8.
Решение: y3 – 3y2 + 6y – 8 = (y3 – 8) – (3y2 -6y) = (y -2) (y2 + 2y + 4) – 3y(y – 2)= (y – 2)(y2 + 2y + 4 – 3y)= (y – 2)(y2 – y + 4)/
Комбинировали три приема:
– группировку;
– вынесение общего множителя за скобки;
– использование формул сокращенного умножения.
Эти примеры показывают, что при разложении многочлена на множители полезно соблюдать следующий порядок:
Вынести общий множитель за скобку (если он есть).
Попробовать разложить многочлен на множители по формулам сокращенного умножения.
Попытаться изменить способ группировки (если предыдущие способы не привели к цели).
Пример 4. n3 + 3n2 + 2n.
Решение: n3 + 3n2 + 2n = n (n2 + 3n + 2) = n (n2 + 2n + n + 2) = n ((n2 + 2n) + (n + 2)) = n (n (n + 2) + n + 2) = n (n + 1) (n + 2).
Комбинировали три приема:
– вынесение общего множителя за скобки;
– предварительное преобразование;
– группировку.
Отмечаем, что для решения этого примера мы использовали еще один прием разложения на множители – предварительное преобразование.
Даем ему характеристику
Предварительное преобразование
Некоторый член многочлена раскладывается на необходимые слагаемые или дополняется путем прибавления к нему некоторого слагаемого. В последнем случае, чтобы многочлен не изменился, от него отнимается такое же слагаемое.
Квадратное уравнение имеет вид  + bx + с = 0, а ≠0
+ bx + с = 0, а ≠0
Квадратный трёхчлен раскладывается на множители следующим образом:
ax2 + bx + с = 0 a(x – x1)(x – x2), где x1и x2 – корниквадратного уравнения
Дискриминант: D =  - 4ac
- 4ac
Если D > 0, то кв. ур-е имеет два различных корня, которые могут быть вычислены по формулам:
X1,2 = 
Если D = 0, то квадратное уравнение имеет два равных корня.
Если D < 0, то действительных корней нет.
Заполнить таблицу из 100 квадратных уравнений следующих десяти видов.
Неполные квадратные уравнения:
1) ax2 + bx = 0;
2) ax2 + c = 0; левую часть удобно представить в виде разности квадратов двух выражений;
3) ax2 + c = 0; левую часть неудобно представить в виде разности квадратов двух выражений.
Полные квадратные уравнения, в которых:
4) a + b + c = 0;
5) a – b + c = 0;
6) левая часть уравнения представима в виде квадрата двучлена;
7) приведенное квадратное уравнение;
8) b = 2k;
9) b = 2k – 1;
10) D < 0.
В таблице по 10 уравнений каждого вида. Также в таблице имеются уравнения, в которых:
а) переменная обозначена латинской буквой, отличной от x;
б) записанные не в стандартном виде;
в) уравнения, которые можно упростить, разделив левую и правую части на число, отличное от нуля.
Решите самостоятельно.
1. Вместо знака * поставьте одночлен таким образом, чтобы упростить можно было с помощью формул сокращенного умножения:
a2 +4 ab + *; 9x4 – 6x2 y + *; 100a6 - * + b2; 4x4 – 25y2 =(2* -5*)(2*****)
2. Решите уравнение: x2 – x = 0 2x2 – 4x =0 3x2 – 7x = 0
3. Вычислите наиболее рациональным способом: 532 – 432 1082 – 982  - 67· 52
- 67· 52
4. Найдите значение выражения 2a + b +2a2 + ab, если: a= – 1; b=998; если: a=45,5; b= – 3; если: a=7,4; b= – 2
5. Разложить на множители многочлены:
20x3 y2 + 4x2 y2; 27b3 + a6; 15a3 b +3a2 b3; 2y(x-5) + x(x-5);
b(a +5) – c(a +5); 2an – 5bn – 10bn + am; x2 + 6x +9; 49m2 -25n2 ;
2bx - 3ay -6by + ax; 3a2 +3ab – 7a -7b; a4-b4; a2 +ab – 5a -5b
5a3 – 125ab2; a2 – 2ab + b2 – ac + bc; 63ab3 – 7a2b; m2 + 6mn + 9n2 – m – 3n
x2 + 4x + 3; x3 + 3x2 + 4; x2 – 3x + 2; 12 y 3 – 20 y 2; x 4 – 1;
-5a3 -3a2 –a; 4x 2y+3x2 y2+2xy2; x 3 – 3 x 2 y – 4 xy + 12 y 2; 36 a6 b3 – 96a4 b4 + 64a2b5
y3 – 3y2 + 6y – 8.
6. Раскрыть скобки: (x + 3)(x + 1); (b – c)(b + c) – a(a + 2c); (a – b)(a – b – c); (c – a)(c + a) – b(b – 2a); 5a(a – 5b)(a + 5b); (x2 + 3 – x)(x2 + 3+ x); 7ab(9b2 – a);
(m + 3n)(m + 3n – 1); (b – a – c)(b + a + c); (c – a + b)(с + a – b); (x – 2)(x – 1);
7. Упростить выражения:a)  :
:  б)
б)  +
+  в)
в)  :
: 
г)  -
-  д)
д)  +
+  е)
е)  +
+  ж)
ж)  -
-  з)
з)  +
+ 
и) 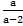 +
+ 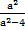 к)
к)  -
- 






