Тема 1.3. Преобразование алгебраических выражений
Самостоятельная работа№3-4 (2 часа)
Цель: научиться применять простейшие формулы и правила алгебраических преобразований.
Тождественные преобразования алгебраических выражений
Понятие алгебраического выражения. Тождество и тождественное преобразование.
Алгебраическим выражением называется совокупность конечного количества чисел, обозначенных буквами или цифрами, соединенных между собой знаками алгебраических действий и знаками последовательности этих действий (скобками).
Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением. Если кроме указанных действий входит действие деления, то выражение называют дробно-рациональным.
Целые рациональные и дробно-рациональные выражения вместе называются рациональными. Если входит еще и действие извлечения корня, то такое выражение называют иррациональным.
Числовым значением алгебраического выражения при заданных числовых значениях букв называют тот результат, который получится после замены букв их числовыми значениями и выполнения указанных в выражении действий.
Областью допустимых значений (ОДЗ) алгебраического выражения называют множество всех допустимых совокупностей значений букв, входящих в это выражение.
Действия над степенями
Действия над степенями производятся по следующим правилам:
= 
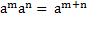
m-n
= amn
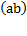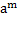
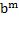
m = 
m =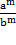 
Одночленом называется алгебраическое выражение, в котором числа и буквы связаны только двумя действиями - умножением и возведением в натуральную степень.
Многочленом называется алгебраическая сумма нескольких одночленов.
Одночлены, из которых состоит многочлен, называются его членами. Одночлен есть частный случай многочлена.
Формулы сокращенного умножения:
а2 – b2 = (a-b)(a + b) –разность квадратов
(a+b)2 =a2 +2 ab + b2 –квадрат суммы
(a-b)2 =a2 -2 ab + b2- квадрат разности
a3 – b3 = (a-b)(a2 + ab + b2) – разность кубов
a3 + b3 = (a+b)(a2 - ab + b2) – сумма кубов
(a+b)3 =a3 +3a2 b +3a b2 +b3 – куб суммы
(a-b)3 =a3 -3a2 b +3a b2 -b3 – куб разности
ax2 + bx + с = 0 a(x – x1)(x – x2)
Квадратное уравнение имеет вид 
+ bx + с = 0, а ≠0
Дискриминант: D = 
- 4ac
Если D > 0, то кв. ур-е имеет два различных корня, которые могут быть вычислены по формулам:
X1,2 = 
Если D = 0, то квадратное уравнение имеет два равных корня.
Если D < 0, то действительных корней нет.
Теорема Виета. В приведенном квадратном уравнении x2 + px + q - 0 сумма корней равна коэффициенту при x, взятому с противоположным знаком, а их произведение – свободному члену:
x1 + x2 = - p; x1 x2 = q
Действия с дробями:
| Сложение | Вычитание | Умножение | Деление |
 +  = 
| - = 
| · = 
| : = 
|
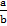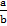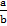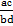
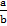Свойства пропорции: 
= 
ad = bc
При работе с модулями используют различные свойства модулей:
≥ 0; 
= 
; 
= 
; 2 = a2; = 
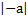
Свойства числовых неравенств:
a≥b 
b≤a;
a≥b и b≥c 
a≥c;
Пусть с 
0 тогда a≥b aс≥bс
Пусть с 
0 тогда a≥b aс≤bс
Пусть a≥b тогда a+с ≥b+с
Пусть a≥b тогда a-с ≥b-с
Примеры решения задач.
1. Упростить выражение: S =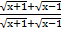 
при x = 
, где a≠b, ab 0
Решение. Покажем прежде, что при заданном условии все подкоренные выражения положительны:
X – 1 = -1 =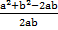 
= 
Поскольку a - b≠0, то 
; ab 0 по условию.
Следовательно, дробь положительна, т.е. x - 1 ;, а значит и x + 1 ;.
Теперь перейдем к упрощению заданного выражения. Освободимся от иррациональности в знаменателе:
S = 
= 
= 
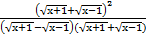= x + 
Подставляя значение x = 
= 
, получим S = + 
= + 
= + 
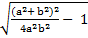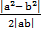
По условию ab 0, значит, = ab, поэтому S = 
Рассмотрим оба возможных случая:
1) если 
, т.е. если 
, то 
= 
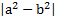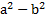и S =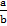
2) если 
, т.е. если 
, то = 
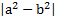и S =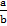
2. Сократить дробь: 
.
Решение. Разложим числитель и знаменатель на множители. Корни числителя: x1 =1; x2= 4, поэтому имеем: 
= (x –x1)(x –x2) =(x –1)(x –4).
Чтобы разложить знаменатель на множители, применим метод группировки:
= (x3 -x)- (4x2 -4) = x(
)- 4() = ()(x -4) = (x -1)(x +1)(x -4)
Тогда при x≠1; x≠-1; x≠4 будем иметь: 
= 
= 
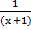
3. Пользуясь теоремой Виета, вычислить: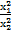 
+ 
, где x1 и x2 - корни уравнения 2x2 +6x +1 = 0 .
Решение. Преобразуем исходное выражение в дробь + =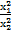 
Числитель данного выражения может быть разложен, как сумма кубов двух выражений: 
= (
)(
). Проведем тождественные преобразования:
()()= ()(
- 3 
) = ()(
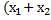)2 - 3 )
Воспользуемся теоремой Виета. Для начала убедимся, что дискриминант квадратного трехчлена 2x2 +6x +1 больше нуля.
Действительно: В = 62 -4·2·1 = 28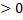 
. Следовательно, у уравнения 2x2 +6x +1 = 0 имеются два действительных корня, и теорема Виета может быть применена.
Таким образом, 
= -3 и =
Поэтому, имеем: + =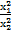 
= 
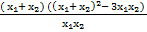= -45
Решить самостоятельно.
1.Упростите выражение: 
: 
2.Найти значение выражения 
при x=31, y=21.
3. Упростите выражение: 
: 
и вычислите его значение при m =-3 и n=7.
4. Найти значение выражения при x=31, y=21.
5. Докажите тождество
- 
+ 
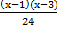= 1
6. Зная, что 
= 10, найдите значение дроби: а) 
; б) 
; в) 
;
7. При каком значении переменной b выражение 3 + 
тождественно равно дроби 
?
Вопросы для самоконтроля.
1.Формулы сокращённого умножения.
2.Правила действий со степенями.
3.Формулы корней сокращённого умножения.
4.Свойства числовых неравенств.
5.Понятие модуля.
6.Свойства пропорции.
