Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Задача заключается в том, чтобы выявить эту общую тенденцию в изменении уровней ряда, освобождённую от действия случайных факторов. Для этого используют следующие методы: метод укрупнения интервалов, метод скользящей средней и метод аналитического выравнивания.
Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Например, ряд ежесуточного выпуска продукции заменяется рядом еженедельного или ежемесячного выпуска. Средняя, исчисленная по укрупнённым интервалам позволяет выявлять направление и характер (ускорение или замедление) основной тенденции развития.
Метод скользящей средней (подвижной средней) состоит в том, что исчисляется средний уровень из определённого числа (обычно нечётного 3, 5, 7) первых по счёту уровней ряда, затем из такого же числа уровней, но начиная со второго по счёту и т.д. Сглаженный ряд не подвержен колебаниям вследствие случайных причин и чётче, в виде некоторой ломаной линии на графике, выражает основную тенденцию развития, связанную с действием долговременно существующих причин и условий развития. Недостатком является «укорачивание» сглаженного ряда по сравнению с фактическим (трёхчленная — на первый член, пятичленная – на первый и последний) и, следовательно, потеря информации.
Метод аналитического выравнивания в рядах динамики заключается в том, что общая тенденция рассчитывается как функция времени:
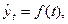
где 
– уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчётных) уровней производится на основе математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики. Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).
Различные виды трендовых моделей, наиболее часто используемых для аналитического выравнивания, приведены в таблице:
| Наименование функции | Вид функции | Система уравнений для нахождения параметров уравнения |
| Линейная |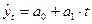 
| 
|
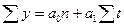
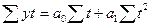
| Парабола второго Порядка | 
| 
|
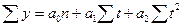
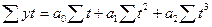
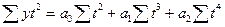
| Парабола третьего Порядка |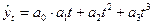 
| 
|
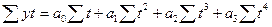
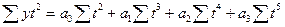
| Показательная |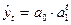 
| 
|
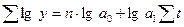
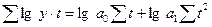
| Гиперболическая | 
| 
|
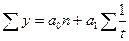
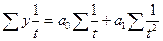
Вычислительный процесс нахождения параметров уравнения при сохранении полной идентичности конечных результатов может быть значительно упрощён, если ввести обозначения дат (периодов) времени (t) с помощью натуральных чисел, с тем, чтобы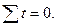 
При выборе формы кривой, наилучшим образом аппроксимирующей эмпирические данные, используется коэффициент аппроксимации:
– среднее квадратическое отклонение эмпирических
уровней ряда динамики от тренда;
– средний эмпирический уровень ряда динамики;
уi – эмпирические уровни ряда динамики;
уt – выравненные (теоретические) уровни ряда динамики;
n – число уровней ряда динамики.
Уравнение тренда выбирается по минимальному значению коэффициента аппроксимации.
После выявления основной тенденции развития явления можно выполнить прогнозные расчёты. Простейшие методы прогнозирования следующие: 1) на основе среднего абсолютного прироста; 2) на основе среднего темпа роста; 3) на основе аналитического выравнивания (трендовой модели).
Модель прогноза по среднему абсолютному приросту имеет вид
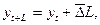
где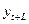 
– экстраполируемый уровень;
– последний уровень периода, за который рассчитан 
;
– средний абсолютный прирост;
L – период упреждения (срок прогноза).
Модель прогноза по среднему темпу роста следующая
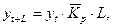
где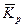 
– средний коэффициент роста.
При прогнозировании на основе аналитического выравнивания применяется адекватная трендовая модель.
Для получения интервальной оценки прогнозного показателя используется формула
где tа – коэффициент доверия по распределению Стьюдента (приложение Б);
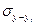– остаточное среднее квадратическое отклонение, скорректированное по числу степеней свободы (n-m).
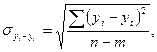
где n – число уровней базисного ряда динамики;
m – число параметров трендовой модели.
