(28) жүйесі үшін Якоби әдісі келесі түрде жазылады
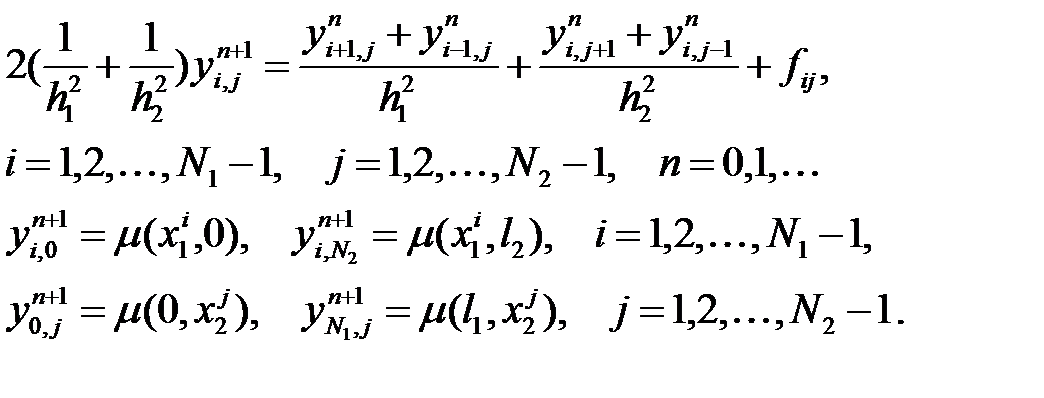(29)
мұнда 
- n-інші итерация бойынша 
нүктесіндегі мәні, ал 
- n+1-інші.
Якоби әдісі нақты берілгенге жету 
итерациясын талап етеді. Бұл өте ақырын жүретін жинақтылық.
(29) жүйеге қатысты Зейдель әдісін қарастырамыз. Жалпы жағдайда Зейдель әдісі і номерлі белгісізі теңдеуде индекстен тұратын, і-ден үлкен, n-інші итерация мәнінің есептеуімен құрылады.
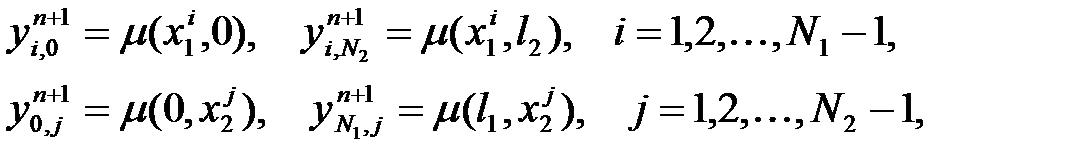(30)
Зейдель әдісі негізінде айқын емес болып табылады, жаңа итерацияда 
мәнін табу қиындық тудырмайды, себебі ол үшбұрышты матрицаға қарайды. Мұнда тек берілген есептерді дұрыс орналастыру қажет.
Зейдель әдісі Якоби әдісінен қарағанда әлдеқайда жылдам байланысады, бірақ берілген нақтылыққа жету үшін итерация саны мұнда 
ретті өлшемімен сәйкес келеді.
Мысал
Тор әдісін пайдаланып, дифференциалды Лаплас теңдеуін 
берілген шекаралық шарттарды шешуді құрастырамыз, қадамдары h=1, 
, 
Шешуі:
Г аймағы OY осіне қатысты симметриялы, сондықтан тек бірінші ширек қаралады. Г шекарасын құрамыз. Сурет 3 қараймыз.
| А |
| B |
| C |
| D |
| E |
| U1 |
| U2 |
| U3 |
| U4 |
| U5 |
| U6 |
| U7 |
Сурет 3. Г аймағы.
h=1 қадамды тор құрамыз.
Шекарада u(x,y) функциясының мәнін есептейміз, 3 кесте:
3 кесте. Шекарадағы функцияның мәні
| Нүкте | A | B | C | D | E |
| x | |||||
| y | 1,7 | 1,4 | |||
| u(x,y) | 2,45 | 2,98 | 3,5 |
Функцияның u(x,y) мәнін анықтау үшін ішкі нүктеде осы мәндерден тұратын теңдеу жүйесін құрамыз. Әрбір теңдеу келесі айырым схемасынан пайда болады:
Сызықты теңдеудің жүйесі кеесі түрде болады:
Жүйе итерация әдісімен шешілген. Жүйенің шешілуі:
u1=2,55, u2=2,73, u3=3,09, u4=2,73, u5 =2,83, u6=3,13, u7=3,53.
Осылайша, әрбір тор түйіні үшін функция мәні табылады.
8.5 Гиперболалық теңдеу
Толқындық теңдеу.
Айқын схема. Аз ішекті ауытқуға қатысты f(х, t) ұзындығына қатысты есептерді қарастырамыз:
(31)
мұнда u(x,t) – ізделіп отырған функция, t уақыт аралығындағы х координатасы бойынша сипатталатын ішек ауытқуының нүктесі.
(34) теңдеуі бастапқы шарттармен қосымшаланады:
(32)
Сонымен қатар параметрлік шарттармен
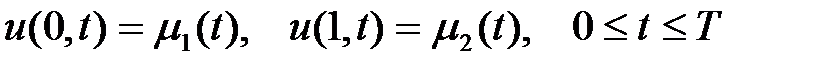(33)
(32) шартының физикалық мағынасы былай қорытындылады: t=0 бастапқы уақыт аралығында х координатасының әрбір нүктесінде u(x) теңдік күйінің ауытқуымен белгілі және ut(x) осы ауытқудың жылдамдығымен өзгереді. (33) шарты ішектің соңы 
- сол жақ соңы, немесе 
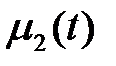- оң жақ соңы заңы бойынша қозғалуы керек екенін білдіреді.
Әдеттегідей, торды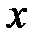 
: 
айнымалыларымен толтырамыз және торды 
айнымалысының 
қадамымен белгілейміз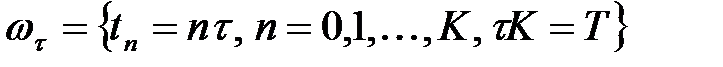 
.
нүктелері кеңістік уақыт торының түйінімен құрастырылады 
, сурет 4.
| 0 |
| tn |
| T |
| 1 |
| xi |
| t |
| h |
Сурет 4. Кеңістік уақыт торы.
y(x,t) функциясы 
торында анықталған, 
белгілеу енгіземіз.
(31) қарапайым айырым аппроксимациясының теңдеуі және (33) шарты келесі жүйе теңдеуі болып табылады:
, (34)
(35)
(34) айырым теңдеуі екінші ретті қателік аппроксимациясы τ және h бойынша сипатталды.
шешу айқын түрдегі мәндер арқылы алдыңғы қабаттарда көрсетіледі:
(36)
Нөлінші қабатта бастапқы шарттан белгілі шешім қолданылады (32):
(37)
Егер (32) бастапқы шартын екінші айырым аппроксимациясымен алмастырсақ,
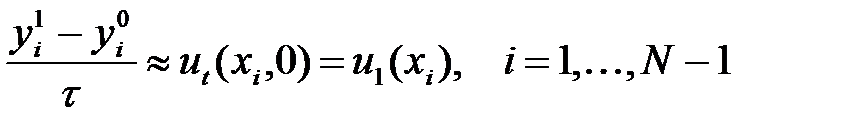(38)
онда τ бойынша бірінші аппроксимацияны аламыз. (34) теңдеуі (31) теңдеуін екінші ретте аппроксимациялайды, бастапқы айырым шарты сол сияқты екінші ретпен аппроксимациялануы керек. Ол үшін Тейлор формуласын t=0 нүктесінің аралығында u(x,t) функциясымен қолданылады.
және (31) теңдеуінің күшінде теңдік орындалатынын есте сақтайық
.
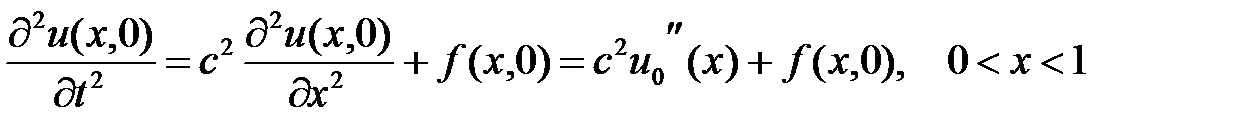Осылайша,
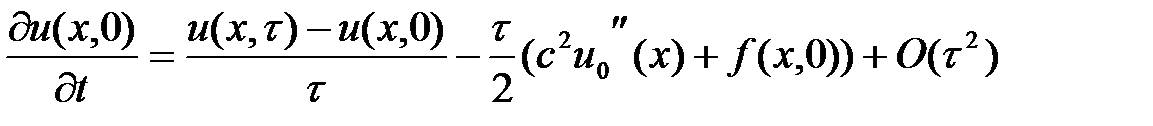
айырым теңдеуі
(39)
(32) шартынан екінші ретте τ және h бойынша аппроксимациялайды.
Осылайша, (31)-(33) есептері үшін келесідей айқын айырым схемасын алдық:
(40)
τ және h бойынша олар екінші ретте аппроксимацияланады. Ол Куранта шартын орындау тұрақтылығы болып табылады:
(41)
(40) схемасы «крест» схемасы деп аталады, себебі ол бес мәнді шаблонды қабылдайды және ол өзінің формасымен крестті еске түсіреді, сурет 5.
| (xi-1,tn) |
| (xi+1,tn) |
| (xi,tn) |
| (xi,tn-1) |
| (xi,tn+1) |
Сурет 5. Крест схемасы.
Айқын емес схема.
(31)-(33) есептері үшін айқын емес схема құрамыз. Сурет 6-дағы суреттегіі шаблонды қарасақ және осыған сәйкес кеңістіктегі әр түрлі туынды қабаттардан схема құрамыз:
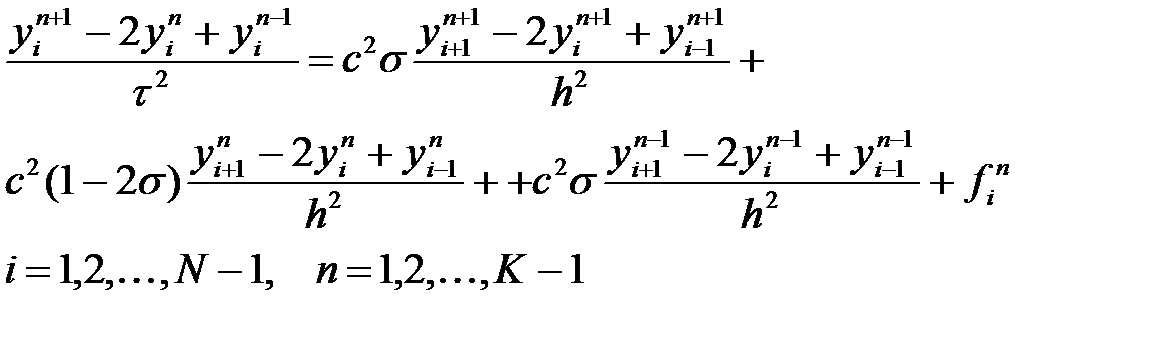(42)
Барлық салмақтар теріс емес, сондықтан 
алу керек.
Шекаралық түйіндерді шешуде (33) шарты бойынша келесі формула арқылы анықталады
(43)
Нөлінші және бірінші қабаттарды шешу мәндері айқын схемада шешілген сияқты (37) және (39) формулалары арқылы өрнектеледі:
(47)
Схеманың (40) қалған қабаттарында (41) шарты бойынша 
-ке қатысты сызықты жүйе теңдеуін үш диагоналды матрица арқылы құрастырады, мұнда диагоналды элементтер басым болады; бұл жүйені шешу жалғыз және қулау әдісімен есептеледі.
Тейлора формуласымен шешу орнатылған, оларды шешу (40)-(42) үздіксіз ширек туындысының схемасымен (31)-(33) теңдеуімен 
кез келген s бойынша аппроксимацияланады.
Тұрақтылық схемасының шарты келесі теңсіздікке ие:
(45)
(45) теңсіздігінен көрінгендей,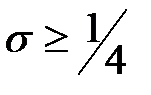 
бойынша (40) схемасы сөзсіз орнықты болып келеді. Егер 
болса, онда схема 
тбойынша шартты орнықты болып табылады.
Осылайша, салмақты таңдау кезінде 
(40) айқын емес схемасы сөзсіз 
сәйкес келеді.
Сурет 6. Айқын емес схемасының шаблоны.
Мысал
Ішекті ауытқуындағы теңдеулер үшін айқын емес схеманы пайдаланып араласқан есепті шешу.
Шешуі:
Уақыт бойынша τ=0,1 қадамды торды және h=0,1 қадамды х кеңістіндегі айнымалыны қарастырайық. Ішекті ауытқуындағы теңдеулер уақыт бойынша екінші туындысын қабылдайды және олардағы қабаттар саны үштен аз болмауы керек.
Теңдеуді аппроксимациялауда айқын емес схеманы қолданамыз.
;
;
;
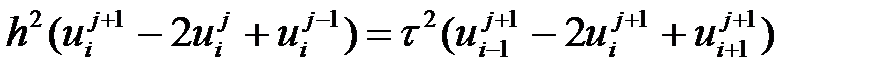Бастапқы шартты аппроксимациялаймыз.
Параметрлік шартты аппроксимациялаймыз.
Осылайша, айырым есебі қойылған:
Бұл есеп қуалау әдісімен шығарылады. Қулаудың сәйкестілік шарты орындалды: 
j=0 және j=1 үшін функцияның мәні бастапқы шарттан табылады, а қалған j мәндері мәні қуалау әдісінің көмегімен табылады.
Қуалаудың нәтижесі j=2 үшін келесі 4 кестеде берілген.
4 кесте. Қуалау әдісінің жүзеге асуы.
| i | xi | ai | bi | ci | αi | βi | yi | fi |
| 0,00 | 0,01 | 0,01 | 0,03 | 0,20 | 0,002 | |||
| 0,10 | 0,01 | 0,01 | 0,03 | 0,00 | 0,20 | 0,30 | 0,003 | |
| 0,20 | 0,01 | 0,01 | 0,03 | 0,33 | 0,17 | 0,40 | 0,004 | |
| 0,30 | 0,01 | 0,01 | 0,03 | 0,38 | 0,21 | 0,50 | 0,005 | |
| 0,40 | 0,01 | 0,01 | 0,03 | 0,38 | 0,27 | 0,60 | 0,006 | |
| 0,50 | 0,01 | 0,01 | 0,03 | 0,38 | 0,33 | 0,70 | 0,007 | |
| 0,60 | 0,01 | 0,01 | 0,03 | 0,38 | 0,39 | 0,80 | 0,008 | |
| 0,70 | 0,01 | 0,01 | 0,03 | 0,38 | 0,46 | 0,90 | 0,009 | |
| 0,80 | 0,01 | 0,01 | 0,03 | 0,38 | 0,52 | 1,00 | 0,01 | |
| 0,90 | 0,01 | 0,01 | 0,03 | 0,38 | 0,58 | 1,10 | 0,011 | |
| 1,00 | 0,01 | 0,01 | 0,03 | 0,38 | 0,64 | 1,20 | 0,012 |
Нәтижесі келесі 5 кестеде көрсетілген.
5 кесте. Есептеудің нәтижесі.
| 1,09 | 1,19 | 1,28 | 1,38 | 1,49 | 1,59 | 1,7 | 1,8 | 1,9 | ||||
| 0,9 | 0,90 | 0,99 | 1,09 | 1,18 | 1,28 | 1,38 | 1,49 | 1,60 | 1,70 | 1,80 | 1,90 | |
| 0,8 | 0,80 | 0,90 | 0,99 | 1,09 | 1,18 | 1,28 | 1,38 | 1,49 | 1,60 | 1,70 | 1,80 | |
| 0,7 | 0,70 | 0,80 | 0,90 | 0,99 | 1,09 | 1,18 | 1,27 | 1,38 | 1,49 | 1,60 | 1,70 | |
| 0,6 | 0,60 | 0,70 | 0,80 | 0,90 | 0,99 | 1,09 | 1,18 | 1,27 | 1,38 | 1,49 | 1,60 | |
| 0,5 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 0,99 | 1,08 | 1,17 | 1,26 | 1,37 | 1,50 | |
| 0,4 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 | 1,09 | 1,14 | 1,26 | 1,40 | |
| 0,3 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,01 | 1,03 | 1,18 | 1,30 | |
| 0,2 | 0,2 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 | 1,10 | 1,20 | |
| 0,1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,1 | ||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||||
| t/x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |||
| j/i |
ДЕБИЕТТЕР ТІЗІМІ
1 Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. - М.- Высшая школа. 1990. -205 с.
2 Демидович Б.П., Марон И.А. Основы вычислительной математики: Учеб. пособие для втузов.- 3-е изд., испр.- М.- Наука. Гл. ред. физ.-мат. лит., 1966.- 664 с.
3 Какенова О.С., Калижанова А.У., Айткулова Ж.С., Кашаганова Г.Б. Вычислительные методы с прменением ЭВМ: Методические указания. –А. – издательский центр КазНТУ, 2002. -90 с.
5 Калиткин Н.Н. Численные методы. - М.-:Наука,1978.-512с.
4 Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах: Учеб. пособие для втузов.- М.- Наука. Гл. ред. физ.-мат. лит., 1972.- 368 с.
5 Марчук Г.И. Методы вычислительной математики: Учеб. пособие.- 3-е изд., перераб. и доп.- М.- Наука. Гл. ред. физ.-мат. лит., 1989.- 608 с.
6 Мастяева И.Н., Семенихина О.Н. Численные методы: Учебное пособие. –М.-МГУЭСИ, 2001. -71 с.
7 Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов.- М.- Наука. Гл. ред. физ.-мат. лит., 1989.- 432 с.
8 Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры.- 2-е изд., испр..- М.: ФИЗМАТЛИТ, 2002.- 320 с.
9 Сегерлинд Л. Применение метода конечных элементов.- М.- Мир, 1976.- 392с.
10 Турчак Л.И. Основы численных методов.- М.: Наука, 1987
