7.1 Шекті-айырымдық әдіс
Екінші ретті қарапайым дифференциалдық теңдеу берілсін:
 (1)
(1)
 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,  - аралығында (1) теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
- аралығында (1) теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
 (2)
(2)
Біз осыған дейінгі есептерде Коши есебі деп дифференциалдық теңдеуге қосымша функцияның бір тәуелсіз айнымалыдағы мәні берілген жағдайды айтып жүрдік. Ал функцияның екі тәуелсіз айнымалыдағы мәндері берілсе, есепті қарапайым дифференциалдық теңдеулер үшін шектік есеп деп айтады.
(1) теңдеу және (2) шекаралық шарттар сызықтық болған жағдайды қарастырамыз:
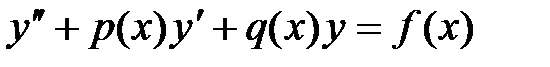 (3)
(3)
 (4)
(4)
 -
-  аралықтағы белгілі функциялар,
аралықтағы белгілі функциялар,  - анықталған тұрақтылар, және
- анықталған тұрақтылар, және  .
.
 аралығында тор енгіземіз:
аралығында тор енгіземіз:
 ,
,
және келесі белгілеме енгіземіз:

(3) дифференциалдық теңдеудегі және (4) шекаралық шарттарындағы туындыларды шекті-айырымды қатынастармен алмастырамыз. Орталық-айырымдық қатынастар қолданамыз. Дифференциалдық теңдеу келесі түрге келтіріледі:
 (5)
(5)
 (6)
(6)
Осы формулаларды қолданып (3) (4) теңдеулерді келесі жүйеге алмастырамыз:
 (7)
(7)
(7) жүйе - n+1 сызықтық теңдеулерден тұратын n+1 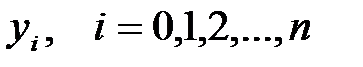 белгісіздері бар жүйе.
белгісіздері бар жүйе. 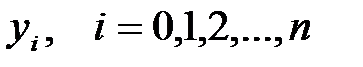 дискретті функция
дискретті функция  функцияны жұықтайды.
функцияны жұықтайды.
Түйінділер саны көп болған жағдайда (7) жүйені сызықтық теңдеулер жүйелерін шешүге арналған әдістерді қолданған тиімді емес, себебі (7) жүйенің үш диагональдағі элементтерінен басқа элементтерінің бәрі нөл. Осындай жүйелер матрицасы үшдиагоналды матрица деп аталады:

Осындай жүйелерді куалау әдісімен шешу тиімді.
Мысал 1
Екінші ретті қарапайым дифференциалдық теңдеу берілсін:
 ,
,
 - айнымалы,
- айнымалы,  аралығында жоғарыдағы теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
аралығында жоғарыдағы теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
 .
.
Шекті-айырымдық әдісті қолданып берілген шектік есептің шешімін табу,  және h=0,1.
және h=0,1.
Шешім:
 - тор енгіземіз.
- тор енгіземіз.
Егер  , онда
, онда  .
.
 белгілеу енгіземіз, және дифференциалдық теңдеудегі туындыларды шекті-айырымды қатынастармен алмастырамыз. Орталық-айырымдық қатынастар қолданамыз. Дифференциалдық теңдеу келесі түрге келтіріледі:
белгілеу енгіземіз, және дифференциалдық теңдеудегі туындыларды шекті-айырымды қатынастармен алмастырамыз. Орталық-айырымдық қатынастар қолданамыз. Дифференциалдық теңдеу келесі түрге келтіріледі:

Шекаралық шарттар келесідей жазылады:

 ,
, 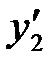 туындыларды шекті-айырымды қатынастармен алмастырамыз:
туындыларды шекті-айырымды қатынастармен алмастырамыз:
 .
.
Яғни, теңдеудің шекаралық шарттар келесідей жазылады:
 .
.
Сонымен  табуға арналған келесі жүйе құрылды:
табуға арналған келесі жүйе құрылды:


Сызықтық теңдеулер жүйесі Гаусс әдісімен шешіледі, 1-кесте.
1-кесте. Гаусс әдісімен жүйені шешу.
| x0-дің коэффициенті | x1-дің коэффициенті | x2-нің коэффициенті | x4-тің коэффициенті | Бос мүше |
| 2,1 | -2 | 0,1 | ||
| 89,5 | -200,76 | 110,5 | 1,5 | |
| -200,55 | 1,5 | |||
| -1 | 1,1 | 0,215 | ||
| 1,000 | -0,952 | 0,048 | ||
| -115,522 | 110,500 | -2,762 | ||
| 89,000 | -200,550 | 111,000 | 1,500 | |
| -1,000 | 1,100 | 0,215 | ||
| 1,000 | -0,957 | 0,024 | ||
| -115,419 | 111,000 | -0,628 | ||
| -1,000 | 1,100 | 0,215 | ||
| 1,000 | -0,962 | 0,005 | ||
| 0,138 | 0,220 | |||
| 1,000 | 1,594 | |||
| Нәтиже: | ||||
| x0=1,472 | x1=1,496 | x2=1,538 | x3=1,594 | |
Мысал 2
Екінші ретті қарапайым дифференциалдық теңдеу берілсін:
 ,
,
 - айнымалы,
- айнымалы,  аралығында жоғарыдағы теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
аралығында жоғарыдағы теңдеуді және осы аралықтың екі шеткі нүктелерінде шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек:
 .
.
Қуалау әдісін қолданып берілген шектік есептің шешімін табу,  және h=0,01.
және h=0,01.
Шешім:
 тор енгізейік. Егер
тор енгізейік. Егер  деп алсақ онда
деп алсақ онда 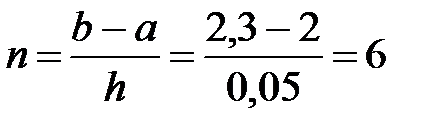 .
.
 белгілейміз және дифференциалдық теңдеудегі туындыларды шекті-айырымды қатынастармен алмастырамыз. Орталық-айырымдық қатынастар қолданамыз. Дифференциалдық теңдеу келесі түрге келтіріледі:
белгілейміз және дифференциалдық теңдеудегі туындыларды шекті-айырымды қатынастармен алмастырамыз. Орталық-айырымдық қатынастар қолданамыз. Дифференциалдық теңдеу келесі түрге келтіріледі:

Ұқсас мүшелерін жинақтау арқылы:
 .
.
Теңдеудің екі жағын да  көбейтеміз:
көбейтеміз:
 .
.
Шекаралық шарттар келесідей жазылады:
 .
.
 туындыны шекті-айырымды қатынастармен алмастырамыз:
туындыны шекті-айырымды қатынастармен алмастырамыз:
 .
.
Яғни, теңдеудің шекаралық шарттар келесідей жазылады:
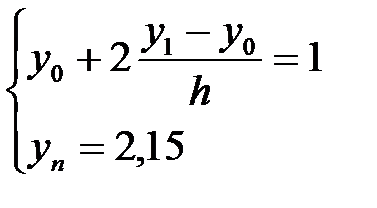 .
.
Ұқсас мүшелерін жинақтау арқылы:
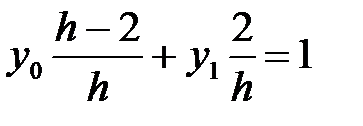 ,
, 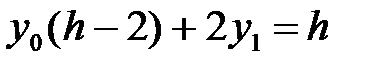 ,
,  .
.
Сонымен  табуға арналған келесі жүйе құрылды:
табуға арналған келесі жүйе құрылды:
 .
.
Осы жүйе - n+1 сызықтық теңдеулерден тұратын n+1 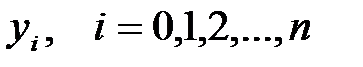 белгісіздері бар жүйе.
белгісіздері бар жүйе. 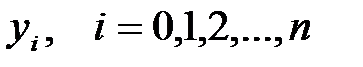 дискретті функция
дискретті функция  функцияны жұықтайды. Осындай жүйелерді қуалау әдісімен шешу тиімді.
функцияны жұықтайды. Осындай жүйелерді қуалау әдісімен шешу тиімді.
Берілген есеп үшін:

Қуалау әдісінің жинақтылық шарты орындалады:

Тура қуалау: Алдымен  коэффициенттерін есептеп табамыз:
коэффициенттерін есептеп табамыз:
 .
.
Осы формулалардың көмегімен  есептеледі.
есептеледі.
Кері қуалау:
Алдымен  есептейміз
есептейміз 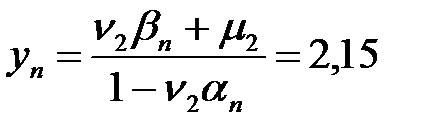 , одан кейін функцияның қалған
, одан кейін функцияның қалған  мәндері табылады:
мәндері табылады:
 .
.
Сонымен:

Есепті шешү қадамдары 2-кестеде көрсетілген.
2- кесте. Қуалау әдісімен есепті шешү.
| xi | ai | bi | ci | alphai | betai | yi | |
| 2,0000 | 0,9900 | 1,0100 | 2,0000 | 2,2348 | |||
| 2,0100 | 0,9900 | 1,0101 | 2,0000 | 1,0050 | -0,0050 | 2,2286 | |
| 2,0200 | 0,9899 | 1,0101 | 2,0000 | 1,0049 | -0,0050 | 2,2228 | |
| 2,0300 | 0,9899 | 1,0102 | 2,0000 | 1,0048 | -0,0051 | 2,2171 | |
| 2,0400 | 0,9898 | 1,0102 | 2,0000 | 1,0047 | -0,0051 | 2,2118 | |
| 2,0500 | 0,9898 | 1,0103 | 2,0000 | 1,0046 | -0,0051 | 2,2067 | |
| 2,0600 | 0,9897 | 1,0103 | 2,0000 | 1,0045 | -0,0051 | 2,2018 | |
| 2,0700 | 0,9897 | 1,0104 | 2,0000 | 1,0044 | -0,0051 | 2,1972 | |
| 2,0800 | 0,9896 | 1,0104 | 2,0000 | 1,0043 | -0,0052 | 2,1929 | |
| 2,0900 | 0,9896 | 1,0105 | 2,0000 | 1,0042 | -0,0052 | 2,1888 | |
| 2,1000 | 0,9895 | 1,0105 | 2,0000 | 1,0041 | -0,0052 | 2,1849 | |
| 2,1100 | 0,9895 | 1,0106 | 2,0000 | 1,0041 | -0,0052 | 2,1813 | |
| 2,1200 | 0,9894 | 1,0106 | 2,0000 | 1,0040 | -0,0052 | 2,1779 | |
| 2,1300 | 0,9894 | 1,0107 | 2,0000 | 1,0039 | -0,0052 | 2,1747 | |
| 2,1400 | 0,9893 | 1,0107 | 2,0000 | 1,0038 | -0,0052 | 2,1717 | |
| 2,1500 | 0,9893 | 1,0108 | 2,0000 | 1,0037 | -0,0052 | 2,1689 | |
| 2,1600 | 0,9892 | 1,0108 | 2,0000 | 1,0036 | -0,0052 | 2,1664 | |
| 2,1700 | 0,9892 | 1,0109 | 2,0000 | 1,0035 | -0,0053 | 2,1640 | |
| 2,1800 | 0,9891 | 1,0109 | 2,0000 | 1,0034 | -0,0053 | 2,1619 | |
| 2,1900 | 0,9891 | 1,0110 | 2,0000 | 1,0033 | -0,0053 | 2,1599 | |
| 2,2000 | 0,9890 | 1,0110 | 2,0000 | 1,0033 | -0,0053 | 2,1581 | |
| 2,2100 | 0,9890 | 1,0111 | 2,0000 | 1,0032 | -0,0053 | 2,1565 | |
| 2,2200 | 0,9889 | 1,0111 | 2,0000 | 1,0031 | -0,0053 | 2,1551 | |
| 2,2300 | 0,9889 | 1,0112 | 2,0000 | 1,0030 | -0,0053 | 2,1539 | |
| 2,2400 | 0,9888 | 1,0112 | 2,0000 | 1,0029 | -0,0053 | 2,1529 | |
| 2,2500 | 0,9888 | 1,0113 | 2,0000 | 1,0029 | -0,0053 | 2,1520 | |
| 2,2600 | 0,9887 | 1,0113 | 2,0000 | 1,0028 | -0,0053 | 2,1513 | |
| 2,2700 | 0,9887 | 1,0114 | 2,0000 | 1,0027 | -0,0052 | 2,1507 | |
| 2,2800 | 0,9886 | 1,0114 | 2,0000 | 1,0026 | -0,0052 | 2,1503 | |
| 2,2900 | 0,9886 | 1,0115 | 2,0000 | 1,0025 | -0,0052 | 2,1501 | |
| 2,3000 | 0,9885 | 1,0115 | 2,0000 | 1,0025 | -0,0052 | 2,1500 |
Есептелген функцияның графигі 1-сүретте көрсетілген. y функция қойылган шектік есебінің шешімі.
1 -сүрет. Функцияның графигі.






