Бұл есепті сызықты және квадратты регрессия деп те атайды.
Жуықтаушы функцияны келесі түрде іздейміз:
(4.25)
Параметрлер бойынша дербес туындыларды табамыз:
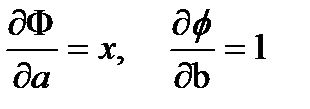
(4.21) түріндегі жүйені құрамыз:
(4.26)
Бұдан
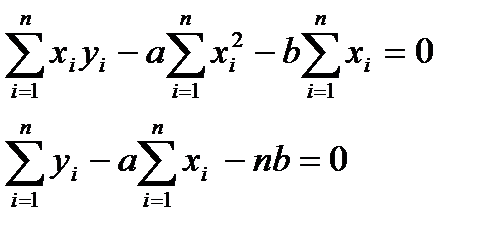
екендігі шығады.
Әрбір теңдеуді n-ға бөлсек:
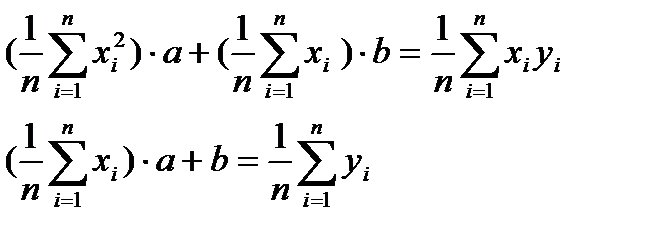(4.27)
Белгілеулер енгіземіз:
Сонда соңғы жүйе мына түрге келеді:
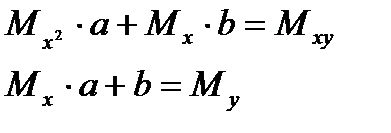(4.28)
Бұл жүйенің коэффициенттері 
-сандарын (4.27)-формуламен есептеп тауып алуға болады. Мұндағы 
-лер кестедегі мәндер. (4.28)-жүйені шешу арқылы a,b-ларды табамыз және (4.25)- сызықты функцияның аналитикалық өрнегін табамыз.
Жуықтаушы функцияны квадрат үшмүшелік түрінде табайық:
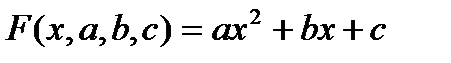(4.29)
Дербес туындыларын табамыз:
.
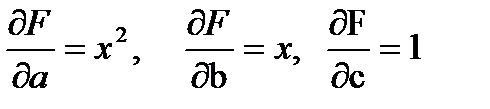(4.21) түріндегі жүйе құрамыз:
Қарапайым ауыстырулардан кейін a,b,c үш белгісізді үш сызықты теңдеуден тұратын жүйе алынады.Алдыңғы әдістегі сияқты жүйені мына түрге келтіреміз:
(4.30)
Мұнда (4.27)–белгілеулері және
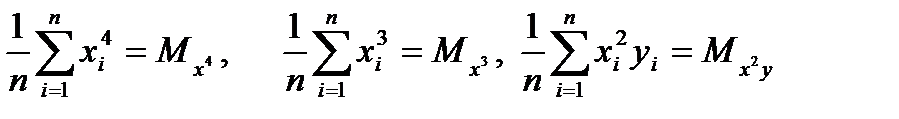(4.31)
белгілеулері қолданылды. (4.30)-жүйеден параметрлер мәндерін және жуыфқтаушы функцияны табуға болады.
Жуықтаушы функцияны дәрежелік функция (геометриялық регрессия) түрінде табу
Жуықтаушы функцияны келесі түрде іздейміз:
(4.32)
(4.16)-кестедегі функция және аргумент мәндері оң деп есептеп (4.32)-теңдікті a>0 шарты бойынша логарифмдейміз:
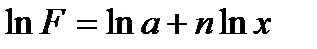(4.33)
F функциясы f функциясына жуықтаушы функция болғандықтан lnF функциясы lnf функциясының жуықтаушысы болады. Жаңа айнымалы енгізейік: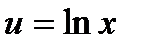 
, онда (4.33)-ден lnF функциясы u: Ф(u) функциясы болады.
M=A, lna=B (4.34)
деп белгілейік, онда (4.33) келесі түрге келеді де есеп сызықты жуықтаушы функцияны табуға келтіріледі:
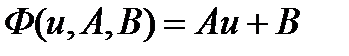(4.35)
Практикада келесі әрекеттерді орындау керек:
1 (4.16)-кесте бойынша х және у мәндерін логарифмдеу арқылы жаңа кесте құру керек.
2 Жаңа кестеден (4.35)-түріндегі жуықтаушы функцияның А, В параметрлерін табу керек.
3 (4.34)-белгілеулерін қолданып a,m параметрлерін тауып, олардың мәндерін (4.32)-ге қою керек.
Жуықтаушы функцияны көрсеткіштік функция түрінде табу
Жуықтаушы функцияны келесі түрде іздейміз:
(4.36)
(4.36)-ны логарифмдейміз:
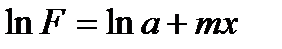(4.37)
(4.34)-белгілеулерді қолданып келесі түрде жазып аламыз:
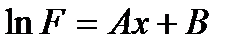(4.38)
Жуықтаушы функцияны (4.36)-түрінде табу үшін кестедегі мәндерді логарифмдеу керек, сосын жаңа кесте құрылады. Жаңа кесте үшін (4.38)-түріндегі жуықтаушы функцияны құру керек. (4.34)-белгілеулерді қолданып a,b параметрлерінің мәндерін тауып (4.36)-ға қою керек.
Жуықтаушы функцияны сызықты-бөлшек функция түрінде іздеу
Жуықтаушы функцияны келесі түрде іздейміз:
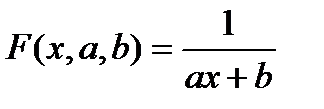(4.39)
(4.39)-теңдікті басқаша жазып аламыз:
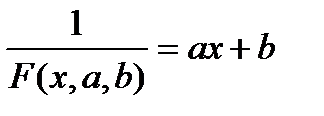
Соңғы теңдіктен a,b параметрлерінің мәндерін табу үшін (4.16)-кестедегі аргументтердің мәндерін өзгертпей, функция мәндерінің орнына кері мәндерді алу арқылы жаңа кесте құрып, жуықтаушы функцияны ax+b түріне құру керек. Сосын параметрлерді тауып (4.39)-ға қояды.
