(4.16)-кесте бойынша сызылған нүктелік график гипербола тарағын беретін болса, онда жуықтаушы функцияны келесі түрде іздеуге болады:
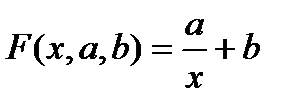(4.41)
Сызықты түрге көшу үшін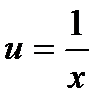 
алмастыруын жасаймыз:
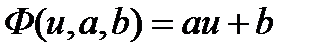(4.42)
(4.16)-кестедегі аргумент мәндерін кері мәндермен ауыстыру керек. Сосын жаңа кесте үшін жуықтаушы функцияны (4.42)-түрінде табу керек. Алынған параметр мәндерін (4.41)-ге қояды.
Мысалы:
| (4.43) |
| |||||
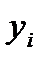
| 4,2 | 2,98 | 2,1 | 0,9 | 0,3 |
Егер осы деректерге сүйеніп график салсақ (3-суретте), оған бір қарағанда пайда болған сызықты түзуге және гиперболаға интерполяциялауға болатыны көрінеді.
| (11.1)-таблица бойынша салынған график |
| (4.43)-таблица бойынша салынған график |
| (4.16)-таблица бойынша салынған график |
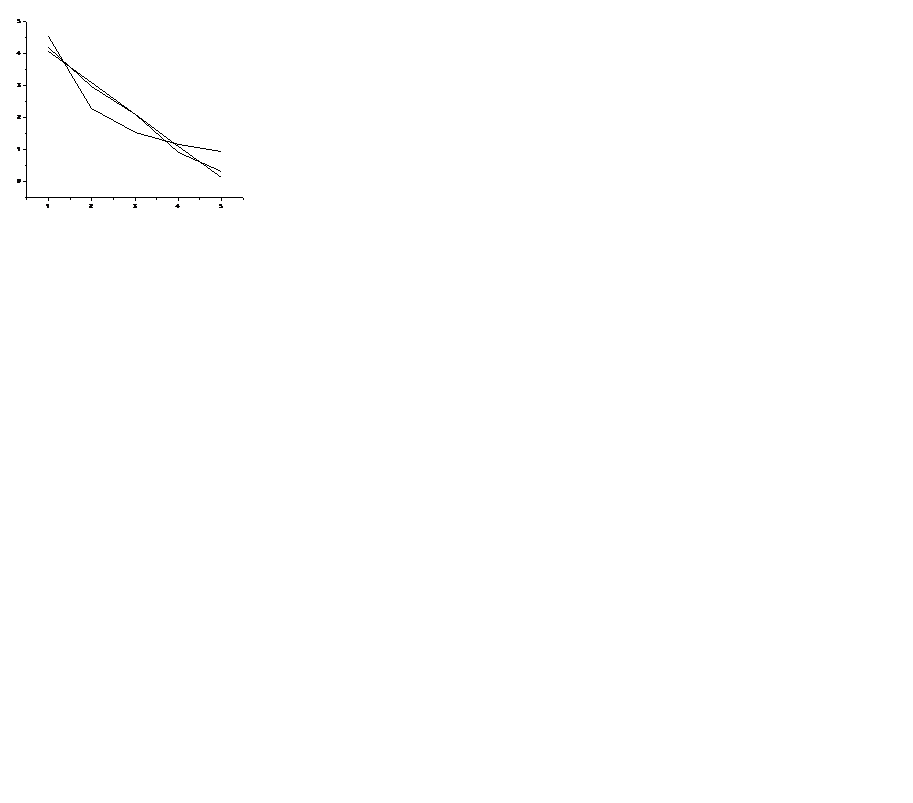
3-сурет – (4.43)-есепте келтірілген деректердің графигі
Ендеше осы екі жағдайды да қарастырып, ауытқулардың квадраттарының қосындыларын салыстыра отырып, қайсысын таңдаған жөн болатынын көрейік.
1 Жуықтаушы функция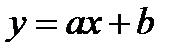 
түріндегі түзу сызық болсын. Осы түзідің 
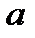және 
параметрлерінің мәндерін анықтайық. 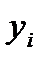мәндерінің 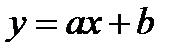түзуінен ауытқуы:
ауытқудың квадраты:
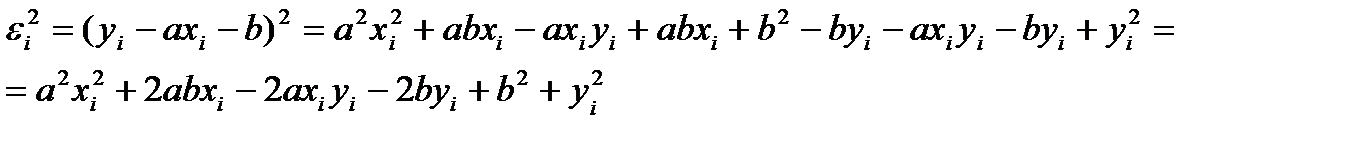
Ауытқулардың квадраттарының қосындысы:
Белгілеулер енгізейік:
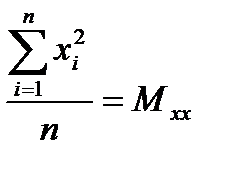
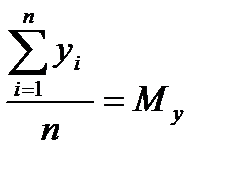
Сонда мына түрге келеміз:
Осы жиыннан 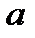және параметрлері бойынша дербес туындылар аламыз және оларды нөлге теңестіреміз:
; 
Теңдеулерді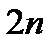 
-ге бөліп мына түрге келеміз:
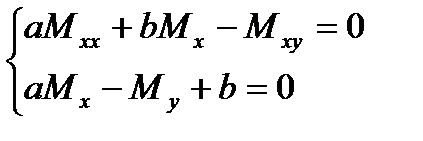
Теңдеулер жүйесін 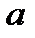және -ға қатысты шешіп мынадай өрнектер аламыз:
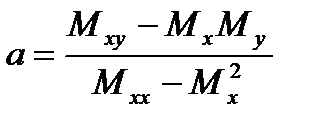
Енді осы алынған нәтижелерді мысалдың басында келтірілген 11-кестеге қолданып көрейік.
11.1-кесте – (4.43)-есепке қою нәтижесі
| 
| |||||
|
| ||||||
|
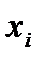
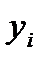
| 4,2 | 2,98 | 2,1 | 0,9 | 0,3 | 10,48 |
| ||||||
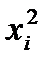
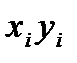
| 4,2 | 5,96 | 3,6 | 3,6 | 2,5 | 21,56 |
Сонымен:
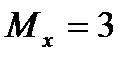
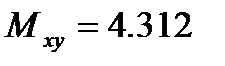
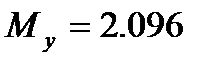
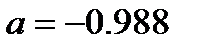
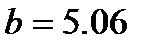
Іздеп отырған түзудің теңдеуі: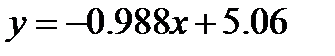 
; 
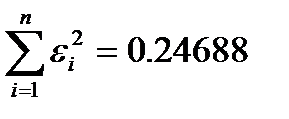
11-кесте – Ауытқулардың квадраттарының қосындысы
|
| ||||||
|
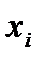
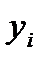
| 4,2 | 2,98 | 2,1 | 0,9 |
| |
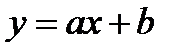
| 4,072 | 3,084 | 2,096 | 1,108 | 0,12 | |
| 0,218 | 0,104 | 0,004 | 0,208 | 0,42 | |
| 0,016384 | 0,010816 | 0,000016 | 0,043264 | 0,1764 |
2 Жуықтаушы функция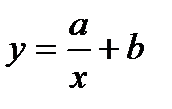 
түріндегі гипербола болатын жағдайды қарастырайық. 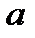және параметрлерін анықтайық. 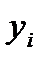мәндерінің 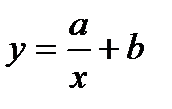гиперболасынан ауытқуы:
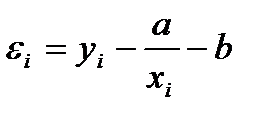
ауытқудың квадраты:
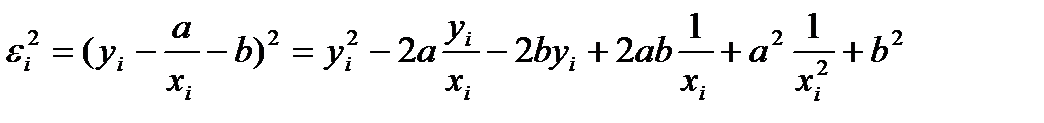
Ауытқулардың квадраттарының қосындысы:
Белгілеулер енгізейік:
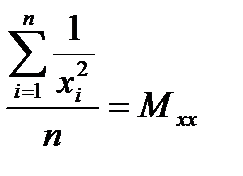
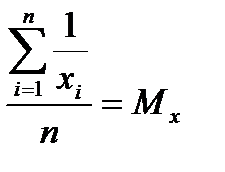
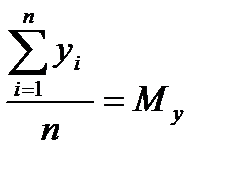
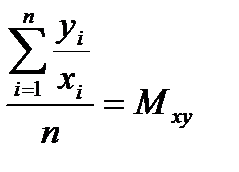
Сонда мына түрге келеміз:
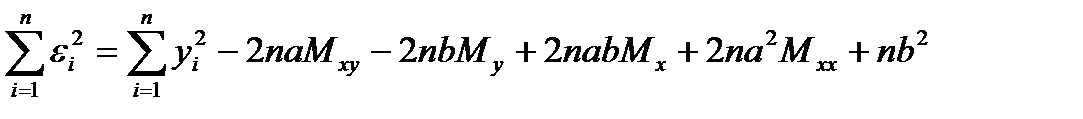
Осы жиыннан және параметрлері бойынша дербес туындылар аламыз және оларды нөлге теңестіреміз:
;
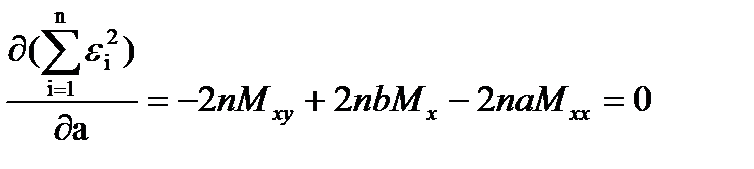Теңдеулерді -ге бөліп мына түрге келеміз:
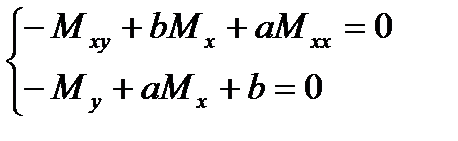
Теңдеулер жүйесін 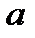және -ға қатысты шешіп мынадай өрнектер аламыз:
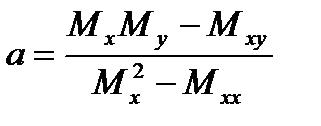
12-кесте – Алынған нәтижелердің кестелік алгоритмі
|
| |||||
|
| ||||||
|
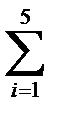
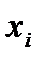
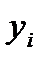
| 4,2 | 2,98 | 2,1 | 0,9 | 0,3 | 10,48 |
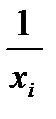
| 0,5 | 0,333(3) | 0,25 | 0,2 | 0,2833(3) | |
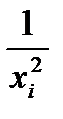
| 0,25 | 0,11111(1) | 0,0625 | 0,04 | 1,4636(1) | |
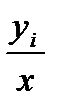
| 4,2 | 1,49 | 0,7 | 0,225 | 0,06 | 6,675 |
Сонымен:
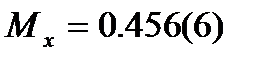
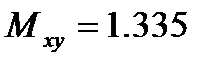
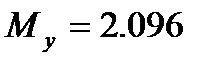
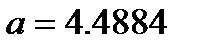
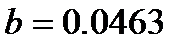
Іздеп отырған гиперболаның теңдеуі:
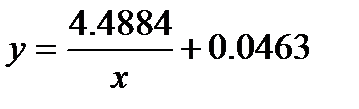
13-кесте – Ауытқулардың квадраттарының қосындысы
|
|
| |||||
|
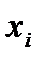
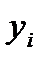
| 4,2 | 2,98 | 2,1 | 0,9 | 0,3 | |
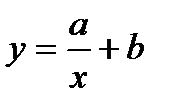
| 4,5347 | 2,2905 | 1,5424 | 1,1684 | 0,94398 | |
|
| 0,3347 | 0,6895 | 0,5576 | 0,2684 | 0,64398 | |
|
| 0,112024 | 0,4754 | 0,31088 | 0,07204 | 0,41471 |
Көрініп тұрғандай, дәл осы жағдайда бірінші таңдаудың дұрыс екендігі даусыз. Жуықтаушы функцияның 
түрінде болатын жағдайын талдауды оқырманның өзіне қалдырдық. Осы мысал көрсеткендей, жуықтаушы функцияны дұрыс таңдап алудың практикалық есептерді шығаруда маңызы зор.
5 ДИФФЕРЕНЦИАЛДЫҚ ЖӘНЕ ИНТЕГРАЛДЫҚ
