Обозначения, которые обычно используют для неприводимых представлений (А, В, Е), были введены Малликенном в 1933г. и с тех пор стали стандартными для спектроскопии и квантовой механики. В этих обозначениях все одномерные представления обозначаются посредством А или В, двумерные – Е, трёхмерные - Т (или иногда F). Неприводимые представления более высокой размерности обозначаются последовательно как G, H и т. д. Отличие А от В связано с характером поведения по отношению к главной оси: представления, симметричные относительно главной оси, являются А -представле-
ниями, а представления, антисимметричные относительно главной оси – В -представлениями. Если имеется несколько представлений определённого типа (А, В, Е или Т), то для их различия вводятся нижние индексы или штрихи в зависимости от поведения представления по отношению к некоторому элементу симметрии.В случае представлений типа А и В индексы 1 и 2 определяют соответственно симметричное и антисимметричное поведение по отношению к оси С2, перпендикулярной к главной оси и к σv или к σd соответственно. Точечные группы D 2 и D 2 h, имеющие три перпендикулярные оси С 2, обладают представлениями В 1, В 2 и В 3, указывающими, какая комбинация ведёт себя симметричным или антисимметричным образом по отношению к этим осям. Выше мы уже обсуждали индексацию для представлений типа Е. Представление Т 1 возникает из преобразования базисных векторов, определяемых матрицами (3.6) – (3.13). Представление Т 2 получается как произведение
Т 2 = А 2  Т 1 Т 1
| (4.32) |
Для всех неприводимых представлений добавляется индекс g (gerade по-немецки – чётный), если система симметрична по отношению к инверсии, и индекс u (ungerade – нечётный), если система антисимметрична. Если задан элемент σh, то один штрих обозначает симметричное поведение по отношению к этому элементу, а два – антисимметричное поведение по отношению к этому элементу. Во избежании двусмысленности обычно используется только вполне определённое число индексов.
С помощью правил, введённых для обозначения неприводимых представлений, можно построить таблицу произведений неприводимых представлений, не используя таблицу характеров. В случае одномерных представлений соответствующая процедура почти тривиальна. Необходимо только помнить, что умножение симметричного характера на симметричный или антисимметричного на антисимметричный даёт симметричный характер, тогда как умножение антисимметричного характера на симметричный даёт антисимметричный характер [т. е. 1  1 = (-1)
1 = (-1)  (-1) и -1
(-1) и -1  1 = -1]. Поэтому получаем
1 = -1]. Поэтому получаем
А  А = В А = В  В = А В = А
| (4.33а) |
А  В = В В = В  А = В А = В
| (4.33б) |
Х 1  Х 1 = Х 2 Х 1 = Х 2  Х 2 = Х 1 Х 2 = Х 1
| (4.33в) |
Х 1  Х 2 = Х 2 Х 2 = Х 2
| (4.33г) |
и т. д. Для произведений, включающих двух- или трёхмерные представления, одних обозначений уже недостаточно для определения таблицы произведений.
Приведённые здесь обозначения неприводимых представлений являются наиболее употребительными. Иногда в литературе встречаются другие обозначения мы их приводить здесь не будем. В некоторых из них для обозначения любого представления используется символ Г, а для того чтобы отличить разные представления, вводятся нижние и верхние индексы.
ЛИТЕРАТУРА
1. Р.Фларри. ГРУППЫ СИММЕТРИИ. Теория и химические приложения. М. – Мир. 1973. 395с. /Перевод с английского канд. физ.-мат. наук Е.С. Крячко./
Приложение
Ответы к некоторым упражнениям
Глава 1
| 1.1 | Векторное сложение
а = (1,2)
b = (2,1)
с= a +b
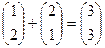 
| 
| |
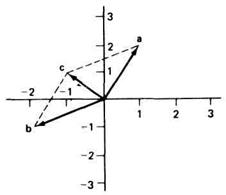
Векторное вычитание
а = (1,2)
b = (2,1)
a - b= с
с = (-1,1)

| 
| ||
Скалярное произведение

|

| ||
| 1.2 | 
| 
| |

| 
| ||

| |||
| 1.6 | 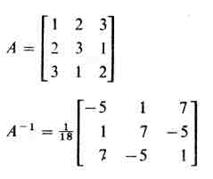
| ||

| |||
| 1.7. а | 
| (учитывать либо верхние, либо нижние знаки) | |
| б | 
| (учитывать либо верхние, либо нижние знаки) | |
| в | 
| ||
| Глава 2 | |||
| 2.1 б | 
| Групповая операция – обычное умножение Свойство замкнутости Выполняется ассоциативный закон Единичный элемент отсутствует | |
| в | 
| Обычное умножение | |

| Замкнутость | ||

| Ассоциативность Единичный элемент Обратный элемент | ||
| г | (Все положительные и отрицательные целые числа, включая нуль) | ||
| Групповая операция - сложение | 1 + 2 = 3 | ||
| целое + целое = целое | |||
| Замкнутость | – целое + – целое = – целое | ||
| – целое + целое = ± целое | |||
| Ассоциативность | 1 + (2 + 3) = (1 + 2) + 3 | ||
| Единичный элемент (нуль) | 1 + 0 = 1 | ||
| Обратный элемент | 1 – 1 = 0 | ||
| 2 – 2 = 0 и т.д. | |||
| д | Все рациональные числа > 0) | Обычное умножение | |
Замкнутость 
| дробь  дробь = дробь или целое число дробь = дробь или целое число
| ||
Ассоциативность 
| |||
Единичный элемент 
| |||

| |||
Обратный элемент 
| |||
| 2.2 | Элементы симметрии | ||
| а) | СН2Сl2 | 
| |
| б) | ВF3

| ||
| в) | Циклогексан

| ||
| 2.5 | Подгруппы | ||
| СН2Сl2 | |||

| |||
| ВF3 | |||

| |||
| Циклогексан | |||

| |||
| 2.7 | 
| 
| |
| СН2Сl2 | |||

| |||
| Глава 3 | |||
| 3.2 | Точечная группа Т | ||
| а) | 
| ||
| б) | Действие оператора на вектор (111) | ||

| |||

| |||
Приложение 6
Глоссарий
Абелева группа. Группа, все элементы которой коммутируют друг с другом и все представления которой одномерны.
Ассоциативный закон композиции. Закон выполняется, если группировка в последовательности операций не существенна, т.е. если
ABCD = (АВ) (CD) = A(BС)D и т.д.
Базисные векторы. Множество векторов, из которых может быть построен любой вектор, принадлежащий этому же векторному пространству.
Базисные функции. Множество функций, из которых может быть построена любая функция из этого же пространства функций.
Вектор. Набор величин а, с одним индексом, обычно располагаемых в виде строки или столбца. Тензор первого порядка.
Возбужденное состояние. Любое состояние системы с энергией, превышающей энергию основного (с наименьшей энергией) состояния. Вырожденные состояния. Независимые состояния, отвечающие одному определенному значению некоторой физической величины, определяющей состояние (такой, как энергия). Число таких состояний называется кратностью вырождения этого значения (говорят также «кратность вырождения состояния»).
Генераторы группы. Простейший набор операций, из которого может быть получена вся группа с помощью умножения и возведения в степень.
Гомоморфизм. Отображение вида «много в один» (многозначное отображение).
Группа. Множество элементов с определенным законом композиции (называемым умножением), такое, что: а) умножение ассоциативно, б) группа содержит единичный элемент, в) для каждого элемента группы существует обратный элемент, г) все произведения и степени элементов содержатся в группе.
Диполь перехода. Ожидаемое значение оператора диполя относительно двух различных состояний системы. Прямое поглощение или излучение света системой зависит от диполя перехода.
Двойные группы. Группы, элементы и представления которых пригодны для изучения систем с полуцелым угловым моментом.
Единичный элемент. Элемент группы, не изменяющий систему. Изодинамические операции. Применимые к нежестким молекулам операции, которые переводят молекулу в конформации с такой же энергией, что и у исходной конформации, но которые не являются операциями точечной симметрии.
Изоморфизм. Взаимно-однозначное отображение.
Квантование. Введение дискретных (или квантованных) состояний. Ковариантные векторы. Векторы, для которых матричные и операторные эквиваленты операции записываются в одном и том же порядке; т.е. если R и S – операторы, R и S – их матричные представления и а – вектор, то
R а = Ra
RS а = RSa
Коммутативный закон композиции. Закон выполняется, если порядок действия двух операций несуществен, т.е. если
АВ = ВА
Контравариантные векторы. Векторы, для которых матричные и операторные эквиваленты операции записываются в обратном порядке; т.е. если R и S – операторы, R и S – их матричные представления и а – вектор, то
R а = aR
RS а = aSR
Кронеккера символ. Величина bij равная нулю, если индексы различные, и равная единице, если индексы одинаковые.
Матрица. Система величин аij с двумя индексами. Эта система обычно имеет вид прямоугольной таблицы, причем индекс i нумерует строки и j – столбцы. Тензор второго ранга.
Матричное представление группы. Множество матриц, гомоморфное группе.
Неприводимое представление. Член множества наипростейших возможных матричных представлений группы.
Несобственная ось поворота. Ось, несобственный поворот относительно которой переводит систему в конфигурацию, неотличимую от исходной. Несобственный поворот – это одна операция, состоящая из поворота и отражения в плоскости, перпендикулярной к оси поворота. Нормированные векторы. Векторы (скажем, а), для которых скалярное произведение а - а равно единице.
Нормированные функции. Функции (скажем, а), для которых интеграл ∫ a*adv равен единице.
Ожидаемое значение. Среднее значение физической величины в некотором состоянии. Этот термин обычно используется тогда, когда данная физическая величина не определяет состояние.
Ортогональные векторы. Векторы (скажем, а и b), скалярное произведение которых а ∙ b равно нулю.
Ортогональные функции. Функции (скажем, а и b), длякоторых интеграл ∫ a*bdv равен нулю.
Основное состояние. Самое низкое по энергии (самое стабильное) состояние системы.
Отображение. Связь между членами двух наборов величин.
Плоскость симметрии. Плоскость, отражение относительно которой оставляет систему неизменной.
Подгруппа. Подмножество множества операций группы, удовлетворяющее групповым постулатам.
Представление группы. Множество величин, обладающее теми же самыми мультипликативными свойствами, что и операции группы. Проекционный оператор. Оператор, проектирующий определенную компоненту функции, вектора и т.п. Используется, например, для построения адаптированных по симметрии линейных комбинаций функций.
Пространственные группы. Группы симметрии, включающие трансляции в качестве операций симметрии.
Симметрии операция. Операция, под действием которой система переводится в ориентацию или конфигурацию, неотличимую от начальной ориентации или конфигурации.
Симметрии элемент. Геометрический объект (точка, линия, плоскость), относительно которого выполняется операция симметрии. Симметрическая группа перестановок (степени n). Множество всех перестановок п объектов.
Скалярное произведение (векторов). Произведение двух векторов, результатом которого является скаляр. «Точечное произведение». Собственная функция. Функция, удовлетворяющая уравнению на собственные значения.
Собственное состояние. Состояние, получаемое в результате действия оператора, который соответствует величине, определяющей состояние (такой, как энергия), на функцию или вектор, которые описывают данное состояние системы.
Собственный вектор. Вектор, удовлетворяющий уравнению на собственные значения.
Собственная ось поворота. Ось, простой поворот вокруг которой переводит систему в конфигурацию, неотличимую от начальной.
Состояние. Положение системы, для которого свойство, определяющее систему, полностью определено.
Состояние, запрещенное по Паули. Состояние системы, которое не может быть достигнуто, поскольку соответствующие ограничения на перестановки частиц не могут быть удовлетворены.
Состояние, разрешенное по Паули. Состояние системы, для которого ограничения на перестановку частиц полностью учтены. Обычно имеются в виду состояния, которые описываются антисимметризованной функцией частиц со спином 1/2.
Тензор. Индексированное множество величин aijk. Число индексов, необходимое для определения тензора, называется его рангом (порядком).
Точечная группа. Группа, описывающая симметрию жесткого физического объекта.
Точка инверсии. Точка, инверсия относительно которой оставляет систему неизменной.
Уравнение на собственные значения. Уравнение, выражающее результат действия оператора на функцию или вектор, когда этот результат представляет собой произведение константы (собственного значения) на исходную функцию или вектор.
Характер. След матрицы, представляющей операцию группы.
Характеров таблица. Таблица, в которой приведены характеры различных операций, соответствующие различным неприводимым представлениям группы.
Элемент группы. Произвольный элемент множества, образующего группу.
Эрмитова матрица. Матрица, равная своей транспонированно-сопряженной: Мij = M * ji.
Юнга диаграммы. Диаграммы, выражающие структуру разбиения неприводимых представлений симметрической группы в виде набора блоков.
[1] Верхний индекс (*) означает, что в приложении 1 рассматривается решение данной задачи.
[2] В современной алгебраической литературе используется ещё термин «морфизмы».
[3] Это так называемая таблица Кэли.






