Как говорилось выше, элементы симметрии любой точечной группы могут быть получены из генераторов группы. В качестве генераторов могут быть использованы любые из четырёх элементов симметрии: либо по отдельности, либо в комбинации друг с другом. По крайней мере трёх из них достаточно для описания точечной симметрии любой системы. Например, мы уже знаем, что элементов С 3 и σv достаточно для описания точечной группы С 3v. Процедура систематической классификации систем по отвечающим им точечным группам может быть проведена основе определения всех возможных генераторов.
Если задан только один элемент, отличный от единицы, то он уже определяет точечную симметрию. Точечная группа, имеющая только плоскость симметрии, называется точечной группой С s или S 1, а содержащая только точку инверсии – точечной группой С i или S 2. Все другие точечные группы содержат одну или несколько осей поворота. Часто многие из них объединяют и относят к аксиальным точечным группам. (На самом деле, точечные группы С s и С i можно рассматривать как особые случаи аксиальных точечных групп). Исключением являются системы с симметрией правильного многогранника, такие, как тетраэдр, октаэдр и т. д. Точечные группы с единственной собственной осью поворота как единственным генератором, обозначаются, как и оси (т.е. С 1, С 2, С 3 и т. д.) Точечная группа, содержащая только единицу, рассматривается как их специальный случай, так как С 1 равно Е. Точечные группы, порождённые единственной несобственной осью поворота, обозначаются S n. Последние определены только для чётных n. Если n нечётно, то имеются дополнительные генераторы и система классифицируется с помощью точечной группы более высокой симметрии. С каждой несобственной осью поворота чётного порядка n связана собственная ось порядка 
. (Элемент S 2 эквивалентен точке инверсии; поэтому точечная группа C i часто обозначается как точечная группа S 2).
Все точечные группы, отличные от C i (или S 2), C s, C n и S n, порождены более чем одним генератором. Аксиальные точечные группы основаны на C n - группах, которые являются подгруппами этих групп. Элементы этих групп более высокой симметрии можно определить путём нахождения смежного класса, образованного подгруппой, соответствующей главной оси, по отношению к дополнительному генератору (если такой генератор один). Если необходимо задать два дополнительных генератора, то сначала формируется смежный класс циклической подгруппы по отношению к одному из них. В результате получается расширенная подгруппа всей точечной группы; затем формируется смежный класс этой подгруппы по отношению ко второму генератору – в результате получаем полную группу. Например, D 3d может быть получена с помощью двух операций: сначала образуют смежный класс циклической подгруппы С 3 по отношению к С2 (это даёт подгруппу D 3):
| (3.3а) |
D 3 = 
| (3.3б) |
затем образуем смежный класс D 3 по отношению к i (это даёт всю группу D 3d):
| (3.4а) |
 D 3d = 
| (3.4б) |
Системы, имеющие только одну собственную ось поворота, обладают не более чем одним дополнительным генератором. Он может быть только плоскостью симметрии. Эта плоскость может или содержать собственную ось (σv), или быть перпендикулярной к ней (σ h). В зависимости от этого получаем два типа точечных групп: C nv или C nh соответственно. (Отметим, что группа C s эквивалентна C 1h). У аксиальных точечных групп, имеющих более чем одну собственную ось, дополнительными осями могут быть только оси С2. Они должны быть перпендикулярны главной оси. Одну из этих осей можно выбрать в качестве второго генератора, используемого вместе с главной осью. Аксиальные точечные группы, имеющие генератор Cn и генератор С2, перпендикулярный Cn, обозначаются символом D n. D n -группы могут иметь в качестве дополнительного генератора плоскость симметрии. Она содержит главную ось или ей перпендикулярна. Плоскость симметрии, перпендикулярная главной оси, обозначается как σh. Плоскости симметрии, содержащие главную ось, являются биссектральными плоскостями между парой осей С2 и обозначаются символами σd. D -группы, в состав которых они входят, обозначаются как D nh и D nd соответственно.
Тетраэдр и октаэдр можно построить из куба, причём тетраэдр получается путём построения нескольких плоскостей, проходящих через диагонали граней (рис. 3.1), а октаэдр – плоскостей, определяемых группами из трёх точек в центре каждой из шести граней куба (рис. 3.2). По этой причине эти группы симметрии часто называют кубическими группами.
| 
|
| Рис. 3.1. Построение тетраэдра в кубе | Рис. 3.2. Построение октаэдра в кубе |
Основные генераторы кубических точечных групп – ось С3, совпадающая с диагональю куба, и одна из осей С2, проходящая через центры противоположных граней куба. (Отметим, что эти оси не являются взаимно перпендикулярными). Это единственные генераторы основной тетраэдрической группы Т. Точечная группа T d дополняется генератором S4, совпадающем с осью С2. (Заметим, что 
; поэтому два генератора С3 и S4 достаточны для описания точечной группы T d). T d – точечная группа тетраэдрических молекул типа СН4. Генераторы точечной группы T h – С3, С2, i.
Октаэдрические точечные группы строятся из основной тетраэдрической группы. Группа О дополняется осью С4, совпадающей с С2 группы Т (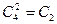
; следовательно, С2 определять необязательно). Группа O h получается добавлением к генераторам группы О точки инверсии. (Это точечная группа октаэдрических комплексов, таких как [Co(CN)6]3-).
Таблица 3.1. Генераторы для различных точечных групп
| Группа | Генераторы | Примечания |
| C n | 
| C 1 – группа порядка1 для систем без симметрии |
| S n | 
| Группа C i эквивалентна (и иногда обозначается как) S 2 |
| C nv C nh | 
| Группа C s эквивалентна (и иногда обозначается как) C 1h |
| D n | 
| Это основная подгруппа всех кубических групп |
| D nd | 
| |
| D nh |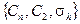 
| |
| T |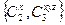 
| |
| T d | 
| Эта группа содержит полную симметрию куба |
| T h | 
| |
| O | 
| |
| O h | 
|
Группы симметрии могут быть получены для систем, основанных на правильных многогранниках, грани которых являются правильными многоугольниками с более чем четырьмя сторонами. Они малоинтересны для химиков, за исключением некоторых полиэдрических боранов, поэтому мы не будем их обсуждать. Генераторы для всех рассмотренных нами типов точечных групп приведены в табл. 3.1. Процедура классификации системы в соответствии с её точечной группой состоит в систематическом поиске всех её возможных генераторов. Иерархия генераторов для классификации точечных групп приведена в табл. 3.2 в обозначениях Шёнфлиса.
Структура произведений точечной группы в основном аналогична структуре генераторов. Например, О h может быть представлена в виде произведения С 3 ^ С 4 × С i. Однако структура генераторов не указывает, является ли произведение прямым или полупрямым. Следовательно, изоморфизмы не могут быть определены только с помощью генераторов.
Рассмотрим теперь на примере D 3 d построение элементов симметрии группы на основе её генераторов. Первым генератором является элемент С 3, образующий циклическую группу С 3 с элементами 
. Второй генератор – это С 2. Смежным классом по отношению к нему является множество из трёх осей С 2, каждая из которых повёрнута на угол 1200 по отношению к другим. Это даёт расширенную подгруппу D 3 ({ E, 2C 3, 3C 2}). Последний генератор – это σd. Смежный класс по отношению к σd содержит произведение циклической группы С 3 с σd, что приводит к трём плоскостям σd, расположенным под углом 1200 относительно друг друга, и произведение операции С 2 с σd. Три элемента, порождаемые этим произведением, трудно непосредственно себе представить. Рассмотрим следующий пример:
| (3.5) |
В результате последовательного применения операций С 2 и σd фигура поворачивается на угол 600 против часовой стрелки и отражается в горизонтальной плоскости (операция S 6). Поэтому тремя элементами, полученными с помощью произведения операции С 2 с σd, являются S 6, 
(или S 2, или i) и 
. В результате для группы D 3 d получаем элементы { E, 2C 3, 3C 2, 3σd, i, 2S 6}.
Упражнение 3.1. Определить все элементы симметрии групп С4 v, D5, D4 d, D5 d. Представить графически один из элементов каждого класса этих групп
Проекционные диаграммы
Для того чтобы лучше представлять себе элементы симметрии на основе соответствующих генераторов, мы будем использовать проекционные диаграммы, представляющие различные возможные аксиальные точечные группы для n, принимающего значения от 1до 6 включительно (рис. 3.3). Главная ось обозначается геометрической фигурой, имеющей собственную поворотную симметрию, и считается перпендикулярной к плоскости рисунка. Несобственная ось, если она имеется, совпадает с главной осью. Плоскость рисунка также содержит σh, если она существует. Остальные генераторы изображены на рисунке: оси второго порядка – крестом, вертикальные плоскости – сплошными линиями.
Если оси С 2 и плоскости σ совмещены, одна половина линии сплошная – другая штриховая. Первый крест показывает произвольную точку системы. Остальные кресты и кружки являются симметрично связанными точками, причём кружки обозначают точки под плоскостью рисунка. Для каждой структуры указаны точечная группа и её генераторы.
Таблица 3.2 Иерархия генераторов для классификации конечных
точечных групп
Рис. 3. 3. Проекционные диаграммы для аксиальных точечных групп с главными осями не выше шестого порядка.
Плоскости симметрии обозначены сплошными линями, оси второго порядка, расположенные в плоскости рисунка – штриховыми. Крестики обозначают точки над плоскостью рисунка.
