При использовании геометрической интерпретации векторов в трёхмерной декартовой системе координат вектор часто представляется совокупностью из трёх чисел, дающих x-, y-, и z- координаты конца вектора по отношению к декартовой системе координат, начало которой совпадает с началом вектора:
| а = (а1а2а3) | (1.9) |
Эта запись означает, что а1, а2, а3 есть числа, на которые нужно умножить единичные векторы i, j, k в направлении осей x, y, и z соответственно, чтобы получить векторную сумму а:
| ai = а1 i + a2 j + a3 k | (1.10) |
Это соотношение графически представлено на рис. 1.6. Отметим, что в уравнении (1.9) мы записали вектор в виде ряда чисел, заключённых в скобки (вектор-строка). (В настоящем изложении вектор-строку мы будем обозначать с помощью верхних индексов). Вектор можно также представить столбцом чисел (вектор-столбец). Например, вектор
| (1.11) |
| |
| Рис. 1.6. Графическое представление вектора а = а1 i + a2 j + a3 k. |
записан как вектор-столбец. (Мы будем обозначать векторы-столбцы нижними индексами). Вектор-строка, имеющий те же элементы, что и е i, называется транспонированным вектором е i и обозначается как 
. Обозначения (1.9) и (1.11) можно обобщить на векторы-столбцы и векторы-строки с любым заданным числом элементов. Вектор, имеющий n элементов, называется n -мерным вектором (по аналогии с трёхмерным вектором). Можно считать, что
n -мерные векторы определяются аналогично (1.10) (согласно уравнению (1.12), где e i обозначают базисные вектора в «n -мерном пространстве»:
| r i = r e1 + r e2 +... + rn e n | (1.12) |
В декартовой системе координат базисные векторы i, j и k являются ортогональными и нормированными (или ортонормированными), т. е. они взаимно перпендикулярны и длина каждого из них равна единице. Однако необязательно выбирать именно такой базис как в трёхмерном, так и в n -мерном пространстве. Вообще любые n некомпланарных векторов можно выбрать в качестве n -мерного базиса. Например, в твёрдом теле часто удобно рассматривать в качестве базиса рёбра элементарной ячейки кристалла, причём только для одной из семи возможных кристаллографических систем все рёбра одинаковы и перпендикулярны.
Представим различные формы векторных комбинаций в неортогональной базисной системе. (Для того чтобы любая комбинация имела смысл, векторы должны быть представлены в одном и том же базисе). Скалярное произведение двух векторов в некотором неортогональном трёхмерном базисе имеет следующий вид:
| a i b i = (a 1e1 + a 2e2 + a 3e3) · (b 1e1 + b 2e2 + b 3e3) = a 1 b 1e1 · e1 + a 1 b 2e1· e2 + a1b 3e1 · e3 + a 2 b 1e2 · e1 + a 2 b 2e2 · e2 + a 2 b 3e2 · e3 + a 3 b 1e3 · e1 + a 3 b 2e3 · e2 + a 3 b 3e3 · e3 | (1.13) |
Для n -мерного случая
| (1.14) |
Векторное и тензорное произведения определяются аналогично. Базисные векторы ортогонального базиса удовлетворяют соотношению
| e i · e j = δ ij | (1.15) |
где δ ij – символ Кронекера, равный единице при i = j и нулю при
i ≠ j.
Скалярные и тензорные произведения векторов легко определяются при их записи в виде вектора-столбца и вектора строки. Умножение вектора строки на вектор-столбец даёт скалярную величину и эквивалентно скалярному произведению:
| a · b = a i b i | (1.16) |
В ортонормированном базисе (который мы обычно будем иметь в виду, если не оговорено иное) имеем
a · b = 
| (1.17) |
| = a 1 b 2 + a 2 b 2 +... + anbn | (1.17a) |
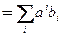
| (1.17б) |
Тензорное произведение выше не было определено, поскольку его можно определить только через элементы векторов. Тензорное (прямое) произведение определяется уравнениями (1.18) и (1.18а):
| (1.18) |
| (1.18а) |
Другим словами, прямое произведение двух n -мерных векторов есть n × n -тензор второго ранга, или матрица С, элементы которой определяются по формуле
| Cij = aibj | (1.19) |
В дальнейшем мы будем часто встречаться с прямым произведением, поэтому рассмотрим один интересный и полезный пример прямого произведения. Рассмотрим прямое произведение единичного вектора а на самого себя, а затем рассмотрим действие этого произведения на другой вектор с. Результат, записанный как 
, может быть сгруппирован справа в 
. Как мы увидим ниже, сгруппированное выражение является по существу иным обозначением скалярного произведения. Таким образом, имеет место соотношение
| (1.20) |
(Заметим, что вектор, умноженной на скаляр, есть вектор имеющий то же направление и величину, равную их численному произведению). Другим словами, в результате получаем вектор, лежащий вдоль а и имеющий величину c cos θ. А это как раз и есть проекция с на а. Поэтому квадрат (в смысле прямого произведения) единичного вектора обычно называют проекционным оператором. Такой квадрат для других векторов даёт аналогичный результат; однако величина проекции будет изменяться с квадратом величины начального вектора:
| (1.21) |
При обозначении векторов через вектор-столбец и вектор-строку запись векторного произведения становиться несколько более сложной, так как не существует непосредственного способа комбинирования векторов-столбцов и векторов-строк для получения вектора, являющегося их произведением. Тем не менее, векторное произведение может быть построено с использованием разложения векторов по базисным векторам. В трёхмерной декартовой системе координат векторное произведение векторов a и b определяется по формуле
a × b = ( a 1 i + a 2 j + a 3 k) × ( b 1 i + b 2 j + b 3 k) =
= a 1 b 1 i × a 1 b 2 i × j + a 1 b 3 i × k + a 2 b 1 j × i + a 2 b 2 j × j
+ a 2 b 3 j × k + a 3 b 1 k × i + a 3 b 2 k ×j + a 3 b 3 k × k (1.22)
Имеют место соотношения
| i × i =0; | i × j = k; | k × i = jи т. д. | (1.23) |
Подставляя эти соотношения в (1.22), получаем
| a × b =(a 2 b 3 – a 3 b 2)i + (a 3 b 1 – a 1 b 3)j + (a 1 b 2 – a 2 b 1)k | (1.22а) |
Формулу (1.22а) можно переписать в более компактном виде через детерминант):
| (1.22б) |
Формулу (1.22) можно использовать для любой размерности при условии, что определено векторное произведение базисных векторов. Однако запись (1.22б) возможна только в трёхмерном случае. Более общий метод включает получение матрицы специального вида (диадики) из одного из векторов и образования её произведения с другим вектором. В обычном трёхмерном пространстве это может быть записано для векторов-столбцов и векторов-строк следующим образом:
| a i × b i = Ab i = – b i × a i | (1.24a) |
| a i × b i = a i B =– b i × a i | (1.24б) |
где А и В – диадики, определённые как
| (1.25а) |
| (1.25б) |
Данные соотношения можно получить путём поэлементного сравнения записи векторного произведения через i, j и k и результата умножения матрицы на векторы (1.24). Этот метод может быть обобщён на случай n измерений; однако при этом результат векторного произведения каждой пары базисных векторов должен быть снова определён.
Упражнение 1.1*. [1] Показать графически эквивалентность геометрического представления векторов и их представления в виде вектора-столбца для сложения, вычитания и скалярного произведения двух векторов.
Упражнение 1.2*. Определить углы между следующими парами векторов трёхмерного пространства:
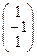и 
; 
и ; 
и ; 
и 
;
и 
Упражнение 1.3*. Определить проекцию вектора
на вектор
Упражнение 1.4. Проверить соотношение (1.24а)
для векторов i, j и k трёхмерного пространства.
Произведение матриц
Соотношение для произведения двух матриц или произведения матрицы и вектора непосредственно следует из (1.16) и (1.17), если рассматривать матрицу либо как столбец, образованный векторами-строками (в том случае, когда она является левым сомножителем), либо как строку, образованную векторами-столбцами (в том случае, когда она – правый сомножитель). Элементы матрицы-произведения можно тогда определить из (1.17). Произвольный элемент такой матрицы имеет вид
| если С = АВ | (1.26а) |
 то 
| (1.26б) |
причём матрицы А и В не обязательно квадратные, однако число столбцов в А должно быть равно числу строк в В. Тогда произведение будет иметь такое же число строк, как и А, и такое же столбцов, как и В. (Заметим, что вектор-строку можно рассматривать как
1 × n -матрицу, вектор-столбец – n × 1-матрицу).
Обратные векторы
Для векторов и матриц понятие деления не определено; для них вводится понятие обратимости. Поэтому выражение a/b не имеет смысла, выражение а · b -1имеет вполне определённый смысл. Выражение
| (1.27) |
справедливо только для скалярных величин. Обратный вектор определяется как вектор, скалярное произведение которого с исходным вектором равно единице. То есть если
| a-1 = b | (1.28а) |
то
| a·b= b·a =1 | (1.28б) |
Однако, если направление вектора не фиксировано, то обратный вектор определён неоднозначно. Обратная матрица вводится как матрица, произведение которой с исходной даёт единичную матрицу, имеющую диагональные элементы, равные единице, недиагональные – нулю.
В обычном декартовом трёхмерном пространстве обратный вектор имеет физический смысл. Это вектор, параллельный исходному и имеющий величину, равную обратной величине исходного вектора. Обратный вектор можно найти при помощи преобразований, которые переводят исходные базисные векторы в обратные. Если u, v и w – набор базисных векторов (не обязательно ортонормированных) в действительном пространстве, то обратные им векторы определяются следующим образом:
| (1.29а) |
| (1.29б) |
| (1.29в) |
Знаменатель этих соотношений является скаляром, который называется тройным скалярным произведением и часто записывается в виде (uvw). (Тройное скалярное произведение (a × b) ∙ с равно объёму параллелепипеда, построенного на векторах a, b и с. Оно равно нулю тогда и только тогда, когда векторы a, b и с компланарны). Числитель в формулах (1.29а – в) есть вектор. Поскольку он выражается через векторное произведение, вектор, обратный каждому базисному вектору, перпендикулярен сопряжённой плоскости соответствующего действительного вектора и необязательно параллелен ему.
Если u, v и w – ортогональный базисный набор и а определяется по формуле
| а = а 1u + a 2v + a 3w | (1.30) |
то вектор, обратный а, равен
| (1.31) |
Произведение е · е – нормирующая константа, равная скалярному произведению базисного набора на себя. Если u, v и w не ортогональны, то обратные векторы всё же можно определить по формуле (1.31), например если отнести вектор а к ортонормированной системе координат с помощью проекционного оператора. Если векторы u, v и w неортогональны, можно выбрать такой базис взаимно ортогональных векторов i, j и k, компоненты вектора а в котором имеют вид
| ai i = i(i · a) =(a 1 u cos θiu + a 2 v cos θiv + a 3 w cos θiw) i i | (1.32a) |
| aj j = j(j · a)= (a 1 u cos θju + a 2 v cos θjv + a 3 w cos θjw) j j | (1.32б) |
| ak k = k(k · a) = (a 1 u cos θku + a 2 v cos θkv + a 3 w cos θkw | (1.32в) |
Вектор а -1 определяется как
| (1.33) |
Можно также построить исходный вектор по отношению к обратному базисному набору. Если мы обозначим действительный базис как е 1, е2, е 3, а обратный ему как е1, е 2, е 3, то
| а = а 1е1 + а 2е2 + а 3е3 = а 1е1 + а 2е2 + а 3е3 | (1.34) |
Отметим условность перемены индексов. Базисный набор в действительном пространстве обозначается нижними индексами, а компоненты произвольного вектора – верхними. И наоборот, базисные векторы в обратном пространстве обозначаются верхними индексами, а компоненты произвольного вектора – нижними. Принятые обозначения в дальнейшем используются для описания преобразований векторов. Векторы, компоненты которых обозначаются верхними индексами, принято называть контравариантными, а векторы, компоненты которых обозначаются нижними индексами – ковариантными.
Упражнение 1.5. В декартовой системе координат оределить векторы, обратные указанным в упражнении 1.2.
Обратные матрицы
Обратная матрица или детерминант могут быть построены безотносительно к базису, хотя при рассмотрении матриц какой-то базис обычно имеется ввиду. Обратная матрица определяется как
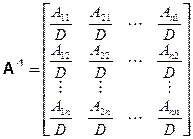
| (1.35) |
В формуле (1.35) D есть детерминант А, т. е. величина, получаемая при полиминальном разложении А по её элементам, Aij – алгебраические дополнения к элементу aij. (Алгебраическое дополнение к элементу (кофактор элемента) aij определяется как детерминант, остающийся после вычёркивания i -строки и j -го столбца из исходного детерминанта и умноженный на (-1) i+j.
Например, если А – 3 × 3-матрица
| (1.36) |
то D – полином
| (1.37) |
Алгебраические дополнения имеют вид
| (1.38а) |
| (1.38б) |
| (1.38в) |
и т.д. Для получения А-1 в явном виде необходимо выражения (1.37) и (1.38) подставить в (1.35). Матрица, детерминант которой равен нулю, не имеет обратной. (Такая матрица называется сингулярной.) Вследствие этого обратные матрицы существуют только для квадратных матриц, поскольку детерминанты для неквадратных матриц не определяются.
Упражнение 1.6*. Найти обратные матрицы для следующих матриц
; 
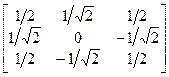
Матрицы и детерминанты
В этом разделе мы остановимся на различии между матрицами и детерминантами. И те и другие представляют собой двумерные множества элементов. Операции матричной алгебры применимы и к детерминантам. Однако между ними имеется одно существенное различие. Если элементы детерминанта – числа, то он имеет вполне определённое числовое значение. Если элементы детерминанта – функции, то детерминант можно представить в виде разложения по этим функциям. С другой стороны, матрица никогда не принимает числового значения и её нельзя представить в виде разложения в ряд. Однако каждой квадратной матрице соответствует определяемый ею детерминант. Матрицы обычно обозначают квадратными скобками, а детерминанты – прямыми линиями.
Наиболее прямой путь вычисления детерминанта – это использование алгебраических дополнений. Детерминант записывают в виде суммы
 ,
| (1.39) |
Где n – порядок соответствующей детерминанту матрицы. Эта процедура повторяется до тех пор, пока алгебраическое дополнение не станет детерминантом 2 x 2. 2 х 2-Детерминант А имеет следующее значение:
 .
| (1.40) |
Ассоциированные матрицы
В дополнение к обратной матрице существует ещё ряд других специальных матриц, ассоциированных с данной. Если А содержит комплексные числа, то матрица А* называется комплексно сопряжённой с А. При этом знак мнимой части каждого элемента А изменяется на обратный. Если матрица А действительная, то А равна А*.
Транспонированная к А матрица 
образуется из А путём замены строк на столбцы 
. Матрица называется симметричной, если А равна , антисимметричной (или кососимметричной), если А равна – . Если к А одновременно применяются операции комплексного сопряжения и транспонирования, то новая матрица А+ называется эрмитово сопряжённой с А. (Иногда в квантовой механике такую матрицу самосопряжённой). Если А равна А+, то она называется просто эрмитовой). Транспонирование, эрмитово сопряжение и образование обратной матрицы от произведения матриц дают соответственно произведения транспонированных, эрмитово сопряжённых и обратных матриц, взятых в обратном порядке:
| (1.41а) |
| (1.41б) |
| (АВ)-1 = В-1А-1 | (1.41в) |
В дополнение к обычному произведению матриц определяется прямое произведение матриц. Если А – квадратная матрица порядка n, В – квадратная матрица порядка m, то прямое произведение
будет квадратной матрицей порядка nm, определяемой следующим образом:
| (1.42) |
Операции транспонирования, эрмитова сопряжения или образования обратной матрицы от прямого сопряжения не изменяют порядка сомножителей:
 и т. д.
| (1.43) |
Унитарные преобразования
Необходимо определить ещё одно понятие в теории матриц, а именно понятие унитарного преобразования. Унитарное преобразование – это преобразование, осуществляемое унитарной матрицей или оператором. Такое преобразование сохраняет скалярное произведение.
Можно показать, что если
| А-1 = А+, | (1.44) |
то столбцы (или строки) матрицы А образуют ортонормированный набор базисных векторов:
| а* i ·а* j = δij | (1.45а) |
| a* i ·a j * = δij, | (1.45б) |
где a* i – i - й вектор-столбец, а i * – i -я вектор-строка. Такая матрица А называется унитарной. Детерминант любой унитарной матрицы равен единице. Рассмотрим, что произойдёт, если унитарную матрицу А умножить на единичный трёхмерный вектор i, направленный по оси х:
 .
| (1.46) |
Этот вектор преобразуется в один из векторов базиса (а *1). Аналогично j преобразуется в а *2 и k – в а *3. Другими словами, система координат x,y,z преобразуется путём поворота в новую систему координат. Аналогично осуществляется преобразование произвольного вектора из одной системы координат (или базиса) к другой. Длина вектора при этом не изменяется, поэтому преобразования этого типа называются унитарными.
Унитарное преобразование А матрицы В осуществляется путём умножения матрицы В слева на А + и справа на А или наоборот:
| В’ = А+ВА. | (1.47) |
Любая эрмитова матрица с помощью подходящего унитарного преобразования может быть диагонализирована, т. е. преобразована в матрицу, у которой не равны нулю только диагональные элементы. Физически это означает такой поворот базиса, при котором все компоненты В (векторы-строки или векторы-столбцы) становятся параллельны соответствующим базисным векторам.
1.9. Преобразование базиса
Выше мы уже дважды упоминали преобразование базисных векторов: преобразование из реального пространства в обратное, рассмотренное в разд. 1.4, и диагонализацию эрмитовой матрицы в разд. 1.8. Последний пример представляет собой специальный случай поворота базиса и полезен для получения общей методики поворота вектора относительно базиса.
Пусть е 1, е 2, е 3 – исходные базисные векторы, 
– базисные векторы, полученные путём поворота и связанные с исходными соотношениями
 ;
| (1.48) |
 ;
| |
 ,
|
содержащим коэффициенты преобразования 
. Если а – произвольный вектор, то его можно записать относительно любого из двух базисов:
 .
| (1.49) |
Компоненты вектора а в исходном базисе связаны достаточно просто с компонентами а в новом базисе и определяются подстановкой (1.48) в (1.49) и приравниванием коэффициентов при е i:
 ;
| (1.50а) |
 ;
| |
 .
|
Длят получения обратного соотношения необходимо ввести новые коэффициенты преобразования:
 ;
| (1.50б) |
 ;
| |
 ,
|
где
| (1.50в) |
здесь 
– символ Кронекера, равный единице при i=k и нулю при
i ≠ k. Коэффициенты 
могут быть найдены подстановкой из (1.48) в (1.50в) и решением, получившейся системы уравнений.
Упражнение 1.7*.
а) Определить такое унитарное преобразование, которое переводит вектор 
в вектор, направленный по оси z, а вектор 
оставляет неизменным, т. е. найти такую матрицу Т,что
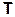
; Т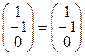 
; Т+Т = 1
б) Определить результат преобразования Т для следующих векторов:
; ; 
в) Определить угол между каждым из векторов в пункте б) и вектором из пункта а) в преобразованной системе координат.
1.10. Вращение вектора: ковариантные и контравариантные
Векторы
Вращение вектора по отношению к системе координат может быть осуществлено двумя способами: либо фиксируется система координат и вращается вектор, либо фиксируется вектор и вращается система координат. Эти операции могут быть записаны с помощью матриц и векторов, причём в обоих случаях конечный результат оказывается одним и тем же.
В уравнении (1.34) разд. 1.4 вектор а был записан через контравариантные компоненты реального пространства, так и через ковариантные компоненты обратного пространства. Это уравнение можно записать, используя записи вектора в виде вектора-столбца и вектора-строки:
 .
| (1.51) |
Если мы определим оператор R, который осуществляет поворот системы координат (в реальном пространстве), согласно уравнению (1.48), то повёрнутый базис 
можно определить следующим образом:
 .
| (1.52) |
(Отметим различие между оператором R и матрицей R.) Если вектор 
фиксирован, то его можно выразить по отношению к повёрнутой системе координат как
 .
| (1.53) |
Результат будет тем же самым, если мы будем вращать вектор и оставим неизменной систему координат:
 .
| (1.54) |
Поэтому матрица, эквивалентная оператору R, действующему на а i, определяется таким образом:
 .
| (1.55) |
То есть результат действия оператора поворота на вектор, эквивалентен произведению вектора на матрицу, представляющую поворот (т. е. порядок матричного представления является обратным порядку операторного представления): отсюда название контравариантный. Однако действительный базис ковариантен по отношению к опрации поворота. Фактически это общее свойство операторов и веторов. Обычный базис преобразуется ковариантым способом, в то время как вектор, определённый в этом базисе, преобразуется контрвариантно. Если операция поворота выполняется в обратном пространстве, обратные базисные векторы должны быть контравариантными, а компоненты а i – ковариантными. Вообще, если u – произвольный вектор-столбец и v – произвольный вектор-строка, то
| для контравариантного вектора R u = Ru | (1.56а) |
| для контравариантного вектора R v = vR | (1.56б) |
Для удобства мы не применяем различных обозначений для ковариантных и контравариантных векторов, если это специально не оговорено.
При использовании ортонормированного базиса контравариантные и ковариантные компоненты совпадают. Это приводит к утверждению о том, что записи вектора в виде вектора-столбца и вектора-строки эквивалентны. При таком предположении произвольный вектор а обычно записывают как вектор-столбец. Тогда вектор а должен быть записан как вектор-строка с теми же самыми элементами, что и у а. В таких обозначениях скалярное произведение записывается как a b и тензорное произведение – как ab; с помощью этих обозначений можно записать и проекционный оператор.
Специально остановимся на двумерных вращениях. В двумерном случае поворот на угол θ представляется матрицей
 .
| (1.57) |
Поворот, обратный данному, есть поворот на угол – θ. Следовательно, если матрица R задана уравнением (1.57), то R -1 имеет вид
R-1 =  .
| (1.58) |
Но так как
| (1.59а) |
и
 ,
| (1.59а) |
то
 .
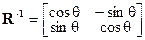| (1.60) |
Таким образом, R -1 равна R + и следовательно, R – унитарная матрица.
В трёх измерениях матрица простого поворота принимает форму
 .
|
(Третье измерение представляет собой ось поворота.)
ГЛАВА II
Cимметрия и группы
Значение симметрии
Многие физические объекты обладают свойственной им симметрией. Рассмотрение этой симметрии помогает исследовать объекты. Например, если бы мы хотели провести полное квантовохимческое изучение молекулы бензола, то нам необходимо было бы полностью описать только одну из её С – Н-связей, а затем, повторяя эту связь, шесть раз, построить шестиугольник. Аналогично, если бы нам понадобилось квантовохимическое описание кристалла какого-нибудь металла, то было бы достаточно полностью описать только одну элементарную ячейку кристалла (в данном случае, как правило, один атом), а затем повторить её во всех направлениях.
Часто поведение объекта при некоторых условиях определяется присущей ему симметрией. На макроскопическом уровне квадратная втулка не может быть подогнана к круглой дырке, так же как и правосторонний болт к левосторонней гайке. На молекулярном уровне биологические организмы весьма чувствительны к симметрии, реагируя на тонкое различие в локальной симметрии D – и L – аминокислот, которые химически идентичны.
Нам известно, что симметрия молекулы или кристалла накладывает ряд ограничений на их взаимодействия с электромагнитным излучением и, следовательно, на их спектральные свойства, а также на дифракционные свойства кристалла. Связи между свойствами симметрии объекта определяют математическую группу. Свойства групп хорошо известны математикам из теории групп; таким образом, симметрия объекта может быть удобно формализована в рамках теории групп.
Существует два подхода к применению теории групп для описания симметрии. Первый состоит в непосредственном использовании образующих функций для рассматривания операций симметрии и построении соответствующих групп симметрии с определёнными групповыми свойствами. Если эти группы найдены, то тогда для выполнения необходимых операций применяются методы теории групп. Второй подход состоит в классификации рассматриваемой системы в соответствии с заранее определёнными группами симметрии. В этом случае соответствующие групповые свойства определяются выбранными группами симметрии. Как и в первом подходе, здесь также используются результаты теории групп.
Первый подход, несомненно, является более эффективным, но для получения необходимых результатов он требует больше знаний и практики, чем второй. В данном изложении теории групп и её приложений мы используем компромиссное решение. В пособии представлен обширный материал по теории и применению образующих функций, а также излагаются основные идеи второго подхода.
Определение группы
Математическая группа может быть определена как множество элементов, обладающих четырьмя основными свойствами. Это следующие свойства:
1. Композиция любых двух элементов группы даёт третий элемент, также принадлежащий группе (свойства замкнутости). Другими словами, если P и Q – элементы группы и их произведение PQ равно S, то S также должно быть элементом группы. Такая композиция называется «произведением», хотя этот термин лишь только в редких случаях имеет тот же смысл, что и в элементарной арифметике. Если в качестве элементов группы взять числа, «произведение» можно определить как любую из арифметических операций: сложение, вычитание, умножение или деление. Однако групповая операция должна быть однозначно определена.
2. Выполняется ассоциативный закон. То есть
| PQRS = P(QR) = (PQ)(RS) и т. д. | (2.1) |
Эти свойства, рассматриваемы совместно, называются групповыми свойствами.
3. Группа должна содержать элемент, коммутирующий с любым другим элементом и оставляющим его неизменным. То есть
| ER = RE = R | (2.2) |
Этот элемент называется единичным элементом и обычно обозначается символом Е. Необходимо отметить, что, вообще говоря, элементы группы коммутируют только с элементом Е. Может, однако случиться, что все элементы группы коммутируют друг с другом; такая группа называется абелевой. Вообще группы симметрии не являются абелевыми; к абелевым группам относятся группы чистых вращений и чистых трансляций.
4. Элемент обратный к элементу группы, также является элементом группы. Если Р – элемент группы, то должен существовать элемент Р –1, такой, что
| P –1 P = RP = PR = PP –1 = E | (2.3) |
В качестве примера рассмотрим группу, которая определяется последней цифрой на любом цифровом счётчике (0, 1, …, 9). Причём произведением элементов является сложением. Элементы этой группы образуют множество {0,1, …, 9}. Число элементов в какой-либо группе называется её порядком. Таким образом, данная группа имеет порядок, равный десяти. Произведение любых двух элементов равно их алгебраической сумме. Поскольку рассматривается только последняя цифра, такое произведение также является элементом указанного множества, которое обладает первым свойством группы. Сложение удовлетворяет ассоциативному закону, поэтому множество обладает вторым свойством группы. (Выполняется также коммутативный закон; следовательно, данная группа абелева.) Нуль является единичным элементом группы: при сложении его с любым элементом группы этот элемент не изменяется. Обратным данному элементу является число, сумма с которым даёт нуль. Например, 9 и 1, 8 и 2, 7 и 3 и т. д. – это элементы, элементы обратные друг к другу. Рассматриваемая группа является примером циклических перестановок. Группа перестановок – это группа, в которой каждый элемент определяется как некоторая перестановка элементов какого-либо множества. Как указывает её название, циклическая перестановка переставляет элементы множества в циклическом порядке, как, например, при переходе от записи {1 2 3 4} → {2 3 4 1}, а затем к {3 4 1 2}. Рассматриваемые ниже группы чистых вращений, относящиеся к группам симметрии, аналогичны группам циклических перестановок. Другие группы симметрии аналогичны группам перестановок иного типа. Фактически любая конечная группа представляется как некоторая группа перестановок (теорема Кэлли).
Упражнение 2.1*. Проверить, что приведённые множества удовлетворяют групповым постулатам в том случае, если операция произведения определена, как указано в каждом случае. Для каждого множества определить единичный элемент.
| Группа | Произведение |
а) 
| Последняя цифра в бинарном сложении |
б) 
| Результат умножения |
в) 
| «« |
| г) Все положительные и отрицательные числа, включая ноль | Результат сложения |
| д) Все рациональные числа больше нуля | Результат умножения |
