Таблицы характеров всех аксиальных точечных групп, являющихся прямыми произведениями их подгрупп, можно построить достаточно просто, применяя понятие генераторов. В диагональных формах матричных представлений операций симметрии, которые приводят к одномерным неприводимым представлениям, все диагональные элементы равны ±1. Это показывает, что операции являются либо симметричными, либо антисимметричными по отношению к различным базисным векторам. Если нам известна таблица характеров подгруппы рассматриваемой группы, то таблицу характеров для группы можно построить путём умножения характеров смежного класса подгруппы по отношению к новому генератору (эти характеры равны ±1) на характеры подгруппы. Например, в точечной группе С 2 v генераторами являются С 2 и σ v. Точечная группа С 2 является подгруппой С 2 v. Смежный класс для этой подгруппы - 
. Если характер σ v принять равным +1, то
| (4.26а) |
| (4.26б) |
| (4.26в) |
| (4.26г) |
Это даёт неприводимые представления:
| Е | С 2 | σ v | 
| (4.27) | |
| А 1 | |||||
| В 1 | -1 | -1 |
Учёт антисимметричного поведения (-1) σ v приводит к значениям
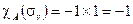
| (4.28а) |
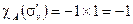
| (4.28б) |
| (4.28в) |
| (4.28г) |
и к неприводимым представлениям:
| Е | С 2 | σ v |
| (4.29) | |
| А 2 | -1 | -1 | |||
| В 2 | -1 | -1 |
Мы получили точно такое же множество неприводимых представлений, что и выше. Таблицу характеров любой другой аксиальной точечной группы, содержащей только прямые произведения, можно получить совершенно аналогичным способом, если известны характеры соответствующих циклических подгрупп. Так же можно построить таблицы характеров аксиальных точечных групп, включающих полупрямые произведения. Для этого необходимо показать, что в таких случаях главную циклическую подгруппу можно выбрать в действительной форме. Все генераторы, за исключением поворотов порядка выше второго, порождают циклические подгруппы второго порядка, и поэтому могут быть описаны представлениями, характеры которых равны ±1
Неприводимые представления и характеры циклических точечных групп (или подгрупп) могут быть построены непосредственно. Основное требование состоит в том, что величина [χ(Cn)] n должна равняться χ(Е), т. е. единице. Это приводит к следующему результату. Для группы С n, если n чётно, существует представление А, представление В и множество представлений Ек, где к принимает значения от 1 до n/ 2 – 1. Все характеры представления А равны +1, тогда как характеры представления В, если оно существует, принимают значения ±1. Характеры для пар вырожденных представлений Ек равны [exp(2 πi/n)] jk и [exp(-2 πi/n)] jk, где к – индекс Ек и j определяется элементом 
. (Это даёт первый элемент е0, т. е. единицу. Отметим также, что представления А и В являются особыми случаями этого представления к, равным 0 и n/2 соответственно). Если представления Е необходимо иметь в действительной форме, то их можно получить путём добавления вырожденных пар мнимых представлений с использованием тригонометрической формы записи экспоненты. Например, в случае точечной группы С 3 можно получить такие представления:
| С3 | Е | С 3 | 
| (4.30) |
| А | ||||
Е 1 
| e2πi/3 | e4πi/3 | ||
| e-2πi/3 | e-4πi/3 |
Они эквивалентны (4.11), если учесть, что поворот на 4π/3, или 2400, полностью эквивалентен повороту на – 2π/3, или на –200. Действительное представление Е получается следующим образом:
| Е | С 3 |
| |||
| Е компл
| Г1 | cos2π/3 + isin2π/3 | cos4π/3 + isin4π/3 | (4.31а) | |
| Г2 | cos2π/3 – isin2π/3 | cos4π/3 – isin4π/3 | (4.31б) | ||
| Г1 + Г2 | 2cos2π/3 | 2cos4π/3 
| (4.31в) | ||
| Е действ | -1 | -1 | (4.31г) |
