К основным понятиям теории вероятности относятся испытания и события.
Под испытанием понимают осуществление некоторого комплекса условий, в результате которого непременно произойдет какое-либо событие. Случайным событием называют такое событие, которое может произойти или не произойти в результате данного испытания.
Например, бросание монеты – испытание, появление герба, появление решки – случайные события. Выстрел по мишени – испытание; попадание, промах - случайные события.
Случайные события обозначают большими буквами латинского алфавита A, B, C, D и т.д. Например, событие А – «выпадение герба при подбрасывании монеты», событие В – «выпадение решки при подбрасывании монеты».
Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение целого числа от 1 до 6 – достоверное событие.
Событие называется невозможным, если оно никогда не произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение 0, выпадение 10 – невозможные события.
События называются несовместными, если никакие два из них не могут появиться одновременно. Если события могут произойти одновременно, то они называются совместными.
Например, подбрасывание игральной кости – испытание, событие А – «выпадение 2», событие В – «выпадение 3», событие С – «выпадение четного числа очков». События А и В, В и С – несовместные, т.к. они не могут произойти одновременно, а события А и С – совместны, т.к. могут произойти одновременно при выпадении числа 2.
События называют равновозможными, если ни одно из них не является объективно более возможным, чем другие.
Так в предыдущем примере события А и В равновозможны, а события В и С, А и С неравновозможны в силу условий проведения испытания.
Множество, элементами которого являются все несовместные равновозможные исходы данного испытания, называют пространством элементарных исходов (событий) и обозначают Ω.
Например, при подбрасывании игральной кости пространство W элементарных событий состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6} (выпадение 1, 2, 3, 4, 5 или 6).
Полная группа событий. Примеры.
По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них.
Определение Править
Пусть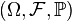 
есть вероятностное пространство. Любое разбиение множества 
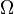элементами сигма-алгебры 
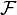называется полной группой событий.
Пример Править
Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:
§ 
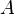: монета упадет орлом;
§ 
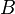: монета упадет решкой;
§ 
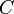: монета упадет на ребро;
§ 
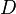: монета зависнет в воздухе.
§ 
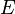: монету притырит подкидывающий
§ 
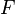: монета превратится в динозавра
§ 
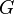: монета станет летающей тарелкой
§ 
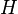: монета так и не преземлится на землю
Таким образом, система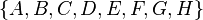 
является полной группой событий.
