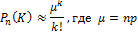О. Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
О. Если события А и В независимы, то вероятность их совмещения равна произведению вероятности этих событий: Р(АВ) = Р(А)* Ра(В)
Теорема сложения вероятностей для совместных событий.
Теорема. Вероятность появления хотя бы одного из совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления: 
.
Формула полной вероятности и формулы Байеса.
Формула полной вероятности.
Формула полной вероятности является следствием основных правил теории вероятностей: теорем сложения и умножения вероятностей.
Допустим, что проводится некоторый опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез):
{ H1, H2, ¼, H n }, Hi Ç Hj =Æ при i ¹ j. (3.1)
Каждая гипотеза осуществляется случайным образом и представляет собой некоторые события, вероятности которых известны:
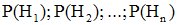. (3.2)
Рассматривается некоторое событие A, которое может появиться только совместно с одной из гипотез (3.2). Заданы условные вероятности события A при каждой из гипотез:
(3.3)
Требуется найти вероятность события A. Для этого представим событие A как сумму n несовместных событий
A = (A ÇH1)È(A ÇH2) È... È(A ÇH n). (3.4)
По правилу сложения вероятностей 
.
По правилу умножения вероятностей P(Hi Ç A)=P(Hi)×P(A / Hi). Тогда полная вероятность события A:
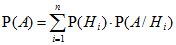, (3.5)
т.е. полная вероятность события A вычисляется как сумма произведений вероятности каждой гипотезы на условную вероятность события при этой гипотезе.
Формула (3.5) называется формулой полной вероятности. Она применяется в тех случая, когда опыт со случайным исходом распадается на два этапа: на первом “разыгрываются” условия опыта, а на втором – его результаты.
Формула Байеса.
Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса.
По условиям опыта известно, что гипотезы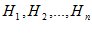 
несовместны, образуют полную группу событий:
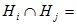Ø при 
и 
.
Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны
; 
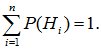
Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза 
(послеопытные вероятности называются апостериорными):
.
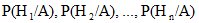Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей:
P(A Ç Hk)=P(Hk)×P(A / Hk)=P(A)×P(Hk / A). (3.6)
Таким образом, можно записать:
P (Hk / A) =P (Hk) ×P (A / Hk)/P (A). (3.7)
С использованием формулы полной вероятности
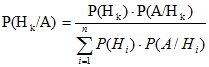. (3.8)
Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А
34. Повторные независимые испытания: постановка задачи, формула Бернулли.
Опр.: некоторые испытания называются независимыми относительно событию А, если вероятность появления события А в каждом исходе не зависит от исходов других испытаний.
Постанова задачи: Пусть производится серия из n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р, а вероятность непоялвения события А также непостоянна и равна q=1-р
Тогда вероятность того, что в этой серии событие А наступит ровно k раз равна:
.
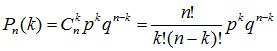35. Локальная теорема Муавра-Лапласа: формулировка теоремы, приближенная формула.
Если испытания удовлетворяют схеме Бернулли, причем n>10, а верностность появления события А в каждом испытании отлична от 0 и 1, то для вычесления вероятности появления события А в n испытаниях ровно k раз используют приближенную формулу из локальной теоремы Муавра- Лапласса:
, где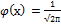 
, 
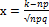
ЧЕТНА!
36. Интегральная теорема Муавра-Лапласа: формулировка теоремы, приближенная формула.
Пусть испытания удовлетворяют схеме Бернулли, n>10, а вероятность появления события А в одном испытании постоянна и отлична от 0и 1.,тогда для определения вероятности того, что событие А появится от K1 до K2 раз, пользуются прибледенной формулой из интегральной теоремы Муавра- Лапласса:
, 
/
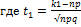НЕЧЕТНА!
37. Теорема Пуассона: формулировка теоремы, приближенная формула.
Если число испытаний велико n>10, а вероятность появления события А в каждом испытании достаточно мала(меньше 0,01), то для вычисления вероятности того, что событие А появится ровно k раз используют приближенную формулу из предельной теоремы Пуассона:
