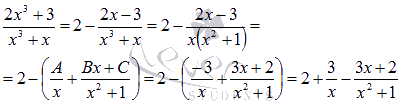· Во-первых, раскладываем знаменатель на множители.
Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители.
В нашем примере все просто – выносим х за скобки.
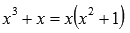
· Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами.
Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.
o Если в знаменателе что-то вроде этого 
, количество линейных множителей роли не играет, (будь их 2 или 22), то дробь представится в виде суммы простейших дробей первого типа:
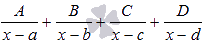
a, b, c и d - числа, A, B, C и D - неопределенные коэффициенты.
o Если в знаменателе что-то вроде этого 
количество множителей роли не играет и не играют роли степени этих множителей (хоть 221ая степень), то дробь представится в виде суммы простейших дробей первого и второго типов:
a, b, c - числа, 
- неопределенные коэффициенты.
Возьмите на заметку: какая степень – столько и слагаемых.
o Если в знаменателе что-то вроде этого 
количество квадратичных выражений роли не играет, то дробь представится в виде суммы простейших дробей третьего типа:
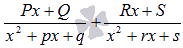
p, q, r и s - числа, P, Q, R и S - неопределенные коэффициенты.
o Если в знаменателе что-то вроде этого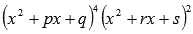 
количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов:
p, q, r и s - числа,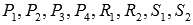 
- неопределенные коэффициенты.
ОБЫЧНО ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ (как правило, довольно простая).
o Если собрать все в кучу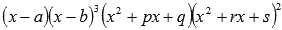 
,то дробь представится в виде суммы простейших дробей всех четырех типов:
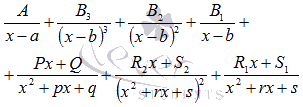
Хватит теории, на практике все равно понятнее.
Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A, B и C.
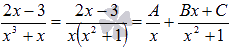
· В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.
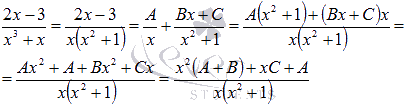
То есть, пришли к равенству:
При x отличных от нуля это равенство сводится к равенству двух многочленов
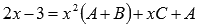
А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.
· В-четвертых, приравниваем коэффициенты при одинаковых степенях х.
При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:
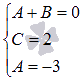
· В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты.
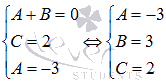
· В-шестых, записываем ответ.
