Однією з найважливіших характеристик САУ є стійкість. Причому, якщо показники точності визначають ступінь корисності і ефективності системи, то від стійкості залежить працездатність системи. Система, що не володіє стійкістю, взагалі не здатна виконувати функції керування і має нульову або навіть негативну ефективність (тобто система шкідлива). Нестійка система може привести керований об'єкт в аварійний стан. Тому проблема стійкості систем є одній з центральних в ТАУ.
Фізичний сенс поняття стійкості. Стійкість автоматичної системи - це властивість системи повертатися в початковий стан рівноваги після припинення впливу, що вивів систему з цього стану рівноваги. Нестійка система не повертається в початковий стан, а безперервно віддаляється від нього.
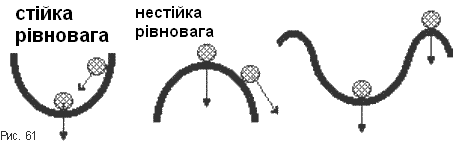
Математична суть стійкості і нестійкості. Згідно даному вище фізичному визначенню стійкість визначається характером руху системи, коли впливи, що вивели її із стану рівноваги, припинили діяти або змінюватися в часі. Такий рух системи називають вільним. Він відбувається за рахунок внутрішньої енергії самої системи і залежить тільки від її властивостей (параметрів).
Вільний рух лінійної або лінеаризованої САУ описується однорідним диференціальним рівнянням
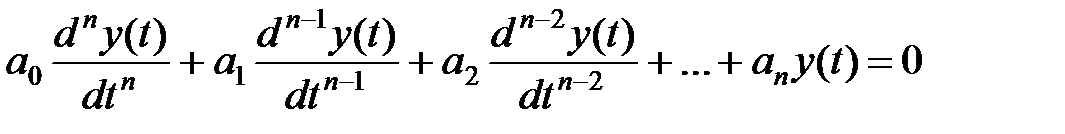(1)
y(t) = yc(t) – вільна складова вихідної величини системи.
Вимушена складова вихідної величини, що залежить від виду зовнішнього впливу і відповідно від правої частини диференціального рівняння системи, на стійкість лінійної системи не впливає.
З математичної точки зору система є стійкою, якщо вільна складова yc(t) перехідного процесу з часом прагне до нуля: 
.
Якщо вільна складова необмежено зростає: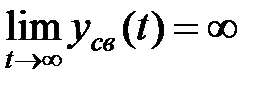 
, то система не стійка.
Якщо вільна складова не прагне ні до нуля, ні до нескінченності, то система знаходиться на межі стійкості: 
.
Вільна складова вихідної величини може бути знайдена як розв’язання відповідного однорідного диференціального рівняння (1) у вигляді суми:
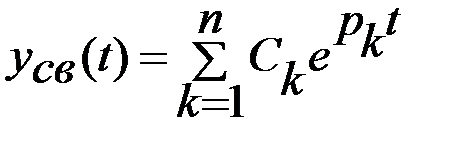(2)
де Ck – постійні інтеграції, залежні від початкових умов;
pk - корні характеристичного рівняння a0pn+ a1pn-1+ a2pn-2+…+ an = 0.
Корінь характеристичного рівняння може бути дійсним (pk = ak), уявними (pk = jbk) і комплексними pk = ak± jbk, причому комплексні корені завжди попарно зв'язані між собою.
Вільна складова (2) при часі t ® ¥ прагне до нуля лише в тому випадку, якщо кожен доданок вигляду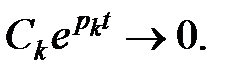 
Характер цієї функції часу залежить від виду кореня pk. Розглянемо всі можливі випадки розташування кореня pk на комплексній площині і відповідні їм функції yс(t), які показані у середині кіл.
1. Кожному дійсному кореню pk = ak в рішенні (2) відповідає доданок вигляду
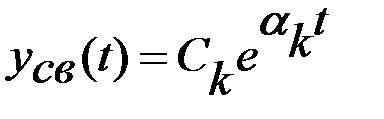. (3)
- якщо ak < 0 (корінь p1), то функція yc(t) при t®¥ прагне до нуля і є убуваючою експонентою;
- якщо ak > 0, то функція yc(t) з часом необмежено зростає - зростаюча експонента (корінь p3);
- якщо ak = 0 (корінь p2), то yc(t) залишається постійною - пряма паралельна осі часу t.
2. Кожній парі комплексно зв'язаних коренів pk = ak+jbk та pk+1 = ak-jbk відповідає вирішення рівняння (1) наступного вигляду:
(4)
Функція yc(t) є синусоїдою з частотою bk і амплітудою, що змінюється в часі як експонента.
- ak < 0 (корінь p5 та p4) – коливальна складова затухатиме.
- ak > 0 (корінь p8 та p9) – амплітуда коливань необмежено зростає.
- ak = 0 (корінь p6 та p7) – обидва корені уявні: pk = +jbk и pk+1 = -jbk, то yc(t) є незгасаючою синусоїдою з частотою bk .
На підставі проведеного аналізу коренів характеристичного рівняння можна сформулювати загальну умову стійкості:
- для стійкості лінійної САК необхідне і достатньо, щоб дійсні частини усіх коренів характеристичного рівняння системи були негативними.
- для стійкості лінійної системи необхідно і достатньо, щоб всі корені характеристичного рівняння знаходилися в лівій півплощині комплексної площини коренів.
Наявність хоч би одного правого кореня робить систему нестійкою.
Стійкість системи залежить тільки від виду кореня характеристичного рівняння і не залежить від характеру зовнішніх впливів на систему. Стійкість є внутрішня властивість системи, що властива їй незалежно від зовнішніх умов.
Уявна вісь jb є межею стійкості в площині коренів. Якщо характеристичне рівняння має одну пару чисто уявних коренів (pk = +jbk и pk+1 = -jbk), а решта усіх коренів знаходиться в лівій напівплощині, то в системі встановлюються незгасаючі гармонійні коливання з круговою частотою w = | bк |. Це коливальна межа стійкості.
Точка b = 0 на уявній осі відповідає нульовому кореню. Якщо рівняння має один нульовий корінь, то система знаходиться на аперіодичній межі стійкості. Якщо таких кореня два, то система нестійка.
