| WУ(p) |
| WОУ(p) |
| x(p) |
| u(p) |
| y(p) |
| f(p) |
| e(p) |
| - |
Призначення будь-якої САУ полягає в підтримці рівності
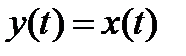
при будь-яких змінах впливів що задають й обурюють. Тобто САУ повинна відтворювати вплив, що задає xз(t) і подавляти (компенсувати) дії впливів, що обурюють. Однак через інерційність об'єкта управління й регулятора обидві ці функції виконуються САУ з погрішністю (помилкою): у кожний момент часу після зовнішнього впливу існує різниця:
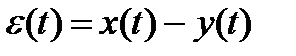
яка й характеризує точністьСАУ. Чим менше миттєві значення помилки e(t), тим вище (краще) точність САУ.
Сигнал помилки e(t) містить складову eз(t), що характеризує точність виконання системою функції відтворення впливу, що задає, і складову eв (t), що характеризує точність виконання функції компенсації збурювань:
.
, 
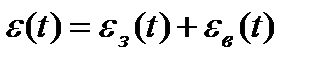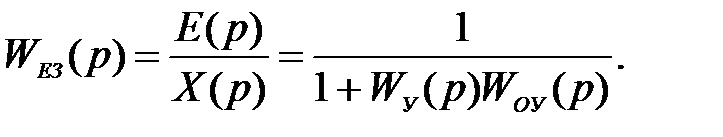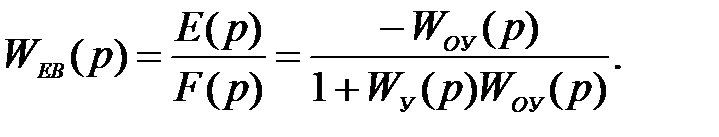
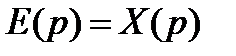
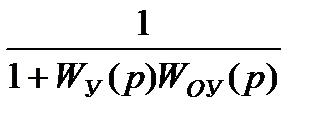
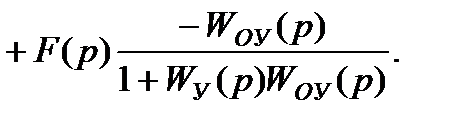
З наведених вище співвідношень випливає одне з найважливіших правил ТАУ:
У типовій одноконтурній системі, що складається з об'єкта W0В(p) і регулятора (керуючого пристрою) WУ(p), повна помилка регулювання e(t) і її складова у статиці й у динаміці обернено пропорційні виразу (1+Wyy(p)W0(p)), тобто точність регулювання тим краще, чим більше підсилювальні властивості регулятора (керуючого пристрою).
Статична точність
У статичному режимі помилки виникають тільки в статичній системі, а в астатичній системі вони дорівнюють нулю. Тому оцінка статичної точності здійснюється при аналізі тільки статичних систем.
Статична система керування – це система, об'єкт і керуючий пристрій якої є статичними елементами, тобто
W0(0) = kОУ, Wy(0) = kУ.
З рівнянь динаміки для сигналу помилки й вихідної величини одержуємо рівняння статики статичної системи підстановкою p=0 і з огляду на те, що W0(0) = kОУ, Wy(0) = ky:
- для керованої величини: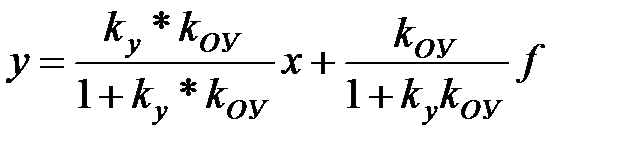 
- для сигналу помилки: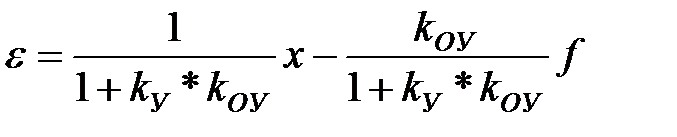 
(*)
Перший доданок у рівнянні (*) характеризує статичну помилку за впливом, що задає, другий - статичну помилку за збуренням. Обидві ці помилки тим більше, чим більше зовнішні впливи, і тем менше, чим більше знаменник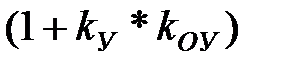 
. Отже:
Точність статичної системи тим краще, чим більше передатний коефіцієнт розімкнутого контуру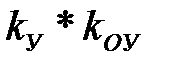 
.
Точність статичної системи прийнято оцінювати коефіцієнтом статизму:
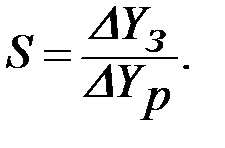
де DYр – відхилення керованої величини y від заданого значення, створюване збурюванням f0 при розімкнутому контурі регулювання;
DYз – відхилення керованої величини y від заданого значення, створюване тим же збурюванням f0 у замкнутій системі.
Коефіцієнт статизму показує у скільки разів відхилення вихідної величини керованого об'єкта менше відхилення цієї величини некерованого об'єкта (при тому самому значенні збурювання).
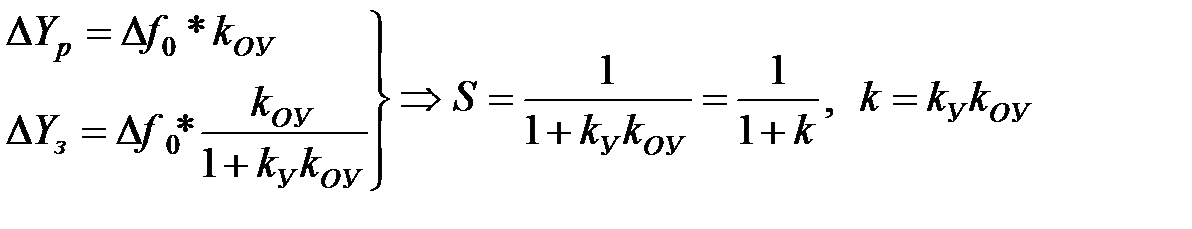
Точність статичної системи задовільна при S = 0,1¸0,01.
Динамічна точність
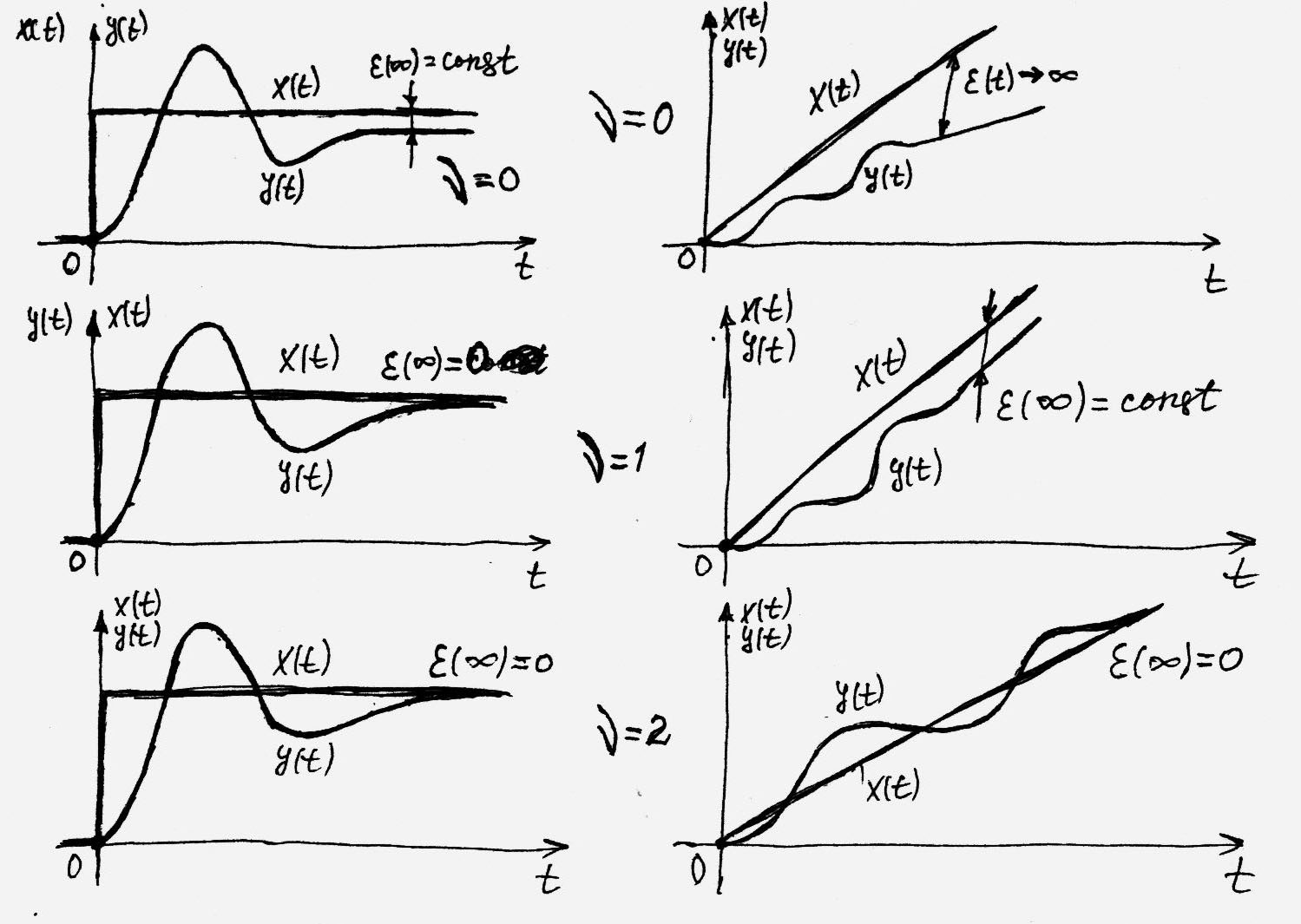
Динамічну точність оцінюють за величиною сигналу помилки в сталому динамічному режимі. У цьому режимі роботи керована величина й сигнал помилки мають тільки змушену складову.
Залежно від властивостей системи й від точки прикладення зовнішнього впливу змушена складова сигналу помилки або дорівнює постійній величині, або необмежено зростає. Постійну змушену складової можна визначити за допомогою теореми про кінцеве значення оригіналу. Зростаючу змушену складову знаходять за допомогою методу коефіцієнтів помилок.
Розглянемо методику визначення постійних складових сигналу помилки.
Визначимо стале значення сигналу помилки типової одноконтурної системи керування при зміні зовнішніх впливів x(t) і f(t) за законом східчастої функції: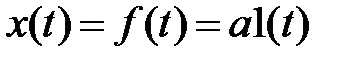 
і за законом статечної функції: 
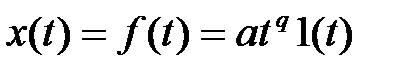, q = 1; 2; 3; ……
Нехай ПФ регулятора й об'єкта має вигляд:
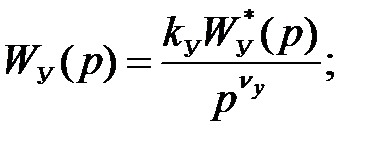
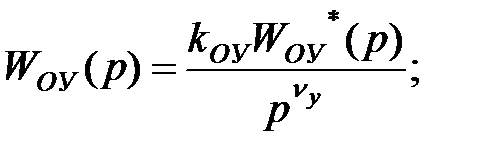
де множник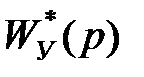и 
й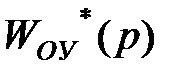 
при p→ 0 прагнуть до одиниці.
Показники nУ и nОУ характеризують порядок астатизму керуючого пристрою й об'єкта.
Типова система керування називається астатичною n-го порядку, якщо вона має астатизм n-го порядку, тобто містить n інтегруючих ланок.
ПФ розімкнутого контуру буде мати вигляд: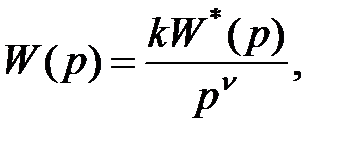 
Де k = kУ*kОУ – передатний коефіцієнт розімкнутого контуру;
n = nВ + nОУ – порядок астатизму системи;
W*(p) = W*В (p)*WОУ*(p) – множник, що при p®0 прагне до одиниці.
Зображення сигналу помилки типової системи одержуємо підстановкою передатних функцій об'єкта управління й керуючого пристрою в рівняння динаміки системи для сигналу помилки:
(**)
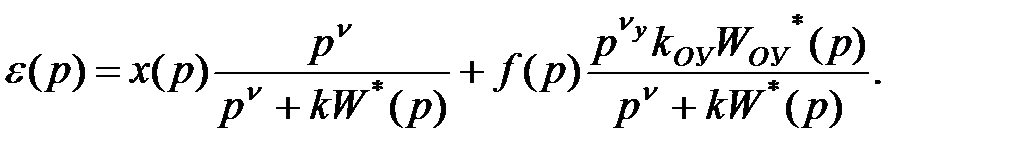З даного вираження виходить, що складова сигналу помилки e, обумовлена зміною впливу, що задає, x(t), залежить від загального порядку астатизму системи n, а складова εв, обумовлена зміною впливу, що обурює, f(t), залежить тільки від порядку астатизму регулятора.
Стале значення сигналу помилки визначається на підставі теореми про кінцеве значення сигналу:
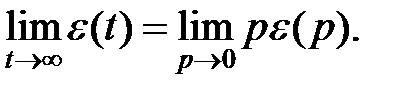
Знаменники обох доданків у вираженні (**) при р®0 прагнуть до значення 1+ k (при n = 0) або до значення k (при n > 0). Граничне значення чисельників залежить від виду функцій x(t) і f(t) і від показників астатизму n і nyy.
Якщо підставити замість x(p) і f(p) у формулі (**) зображення східчастої функції x(p) = f(p) = a/p
або статечної функції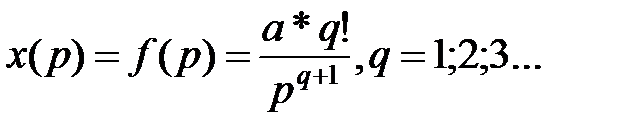 
,
те можна знайти стале значення сигналу помилки.
Сталі значення складових eз і eу для ряду розповсюджених випадків (q =0;1;2 і n = 0;1;2) наведені в таблиці.
| Складова сигналу помилки | Порядок астатизму | Вид впливу | ||
| a(t) | at 1(t) | at2 1(t) | ||
| eз | n = 0 |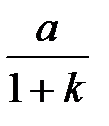 
| ¥ | ¥ |
| n = 1 |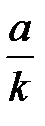 
| ¥ | ||
| n = 2 |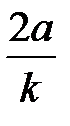 
| |||
| eв | ny=0; nОУ=0 |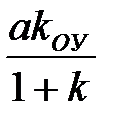 
| ¥ | ¥ |
| ny=0; nОУ=1 |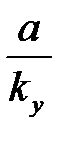 
| ¥ | ¥ | |
| ny=1; nОУ=0 |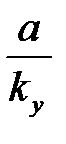 
| ¥ | ||
| ny=1; nОУ=1 |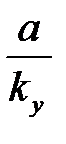 
| ¥ | ||
| ny=2; nОУ=0 |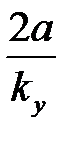 
|
На підставі аналізу результатів, наведених у таблиці, можна сформулювати загальні правила:
1. Якщо сумарний порядок астатизму n типової системи дорівнює показнику q статечного впливу, що задає, то система в сталому режимі має помилку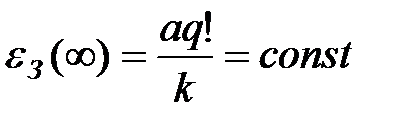 
відтворення, що тим менше, чим більше передатний коефіцієнт розімкнутого контуру системи.
2. Постійна помилка подавлення eв(¥), що виникає в сталому режимі при q = ny, обернено пропорційна передатному коефіцієнту керуючого пристрою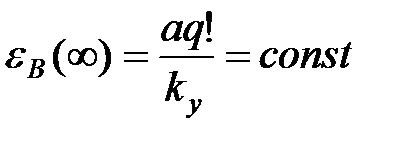 
.
3. Якщо порядок астатизму ny регулятора більше показника q впливу, то стале значення помилки eз(¥) = 0 і eв(¥) = 0.
4. Якщо порядок астатизму n менше показника q, то eз(¥) = ¥ і eв(¥) = ¥.
Перехідні процеси в статичній і астатичній системах при східчастій і лінійній зміні впливу, що задає.
