Чим докладніше математична модель САК, тим вище порядок n її диференціального рівняння. Передавальні функції систем високого порядку (зазвичай n > 4) виявляються громіздкими і незручними для аналізу. Щоб вийти з цього положення, передавальну функцію представляють у вигляді перемноження простих співмножників, порядок яких не перевищує два. Такі співмножники називають типовими ланками.
Безінерційна ланка
Безінерційна (статична) ланка є найпростішою серед всіх типових ланок. Вона передає сигнал з входу на вихід миттєво, без спотворення його форми. У ланці може відбуватися тільки посилення або послаблення вхідного сигналу.
Зв'язок між миттєвими значеннями вхідної величини x(t) і вихідної величини у(t) описується рівнянням алгебри:
y(t) = kx(t).
Передавальні властивості ланки визначаються лише одним параметром - коефіцієнтом передачі k.
Перехідна функція Імпульсна перехідна функція
h(t) = k1(t) w(t) = kd(t)


Рівняння ланки в операційній формі Y(p) = kX(p)
Передаточна функція 
| ω |
| φ(ω) |
| ω=0…∞ |
| P(ω) |
| jQ(ω) |
| A(ω) |
| ω |
| 20lgk |
| ω |
| L(ω) |
| K |
| X(p) |
| Y(p) |
L(w) = 20 lg A(w) = 20 lg k
АЧХ і ФЧХ безінерційної ланки показують, що сигнали будь-якої частоти (0; +¥) проходять через ланку з однаковим відношенням амплітуд вихідної і вхідної величини, рівним k і не мають між собою фазового зсуву.
Прикладами безінерційних ланок є редуктор, датчик потенціометра кутового переміщення, тахогенератор, який використовують як датчик частоти обертання і т. д. Пропорційними ланками моделюються підсилювачі, редуктори, дільники напруги і т. п.
Слід зазначити, що поняття безінерційної ланки є продуктом математичної ідеалізації. Насправді всі реальні конструктивні елементи САК володіють деякою інерційністю, оскільки передача енергії з входу на вихід елементу не може здійснюватися миттєво. Проте, якщо інерційність того або іншого елементу на два-три порядки менша, ніж у решти елементів даної системи, то його вважають безінерційною ланкою.
5.2. Інерційна ланка першого порядку (аперіодична ланка)
Фізично аперіодична ланка містить один елемент, що накопичує енергію, а також один або декілька елементів здатних її розсіювати.
Диференціальне рівняння:
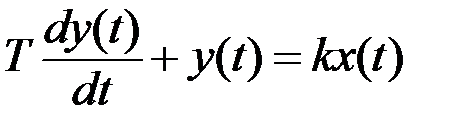
k – коефіцієнт передачі, характеризує властивості ланки в статичному режимі.
Т – постійна часу, характеризує інерційність ланки




Коефіцієнт посилення ланки визначає рівень, до якого прагне перехідна характеристика з часом. Дотична, проведена на початку координат до перехідної характеристики, перетинає цей рівень у момент часу, рівний постійної часу аперіодичної ланки Т. Ці властивості аперіодичної ланки, а також те, що перехідний процес закінчується приблизно за час, що дорівнює 3Т, дозволяє визначати параметри ланки (коефіцієнт посилення і постійну часу) по його експериментальній перехідній характеристиці.
Рівняння ланки в операторній формі (Tp+1)Y(p) = kX(p)
Передаточна функція 
АФЧХ:  АЧХ:
АЧХ: 
| k/2 |
| ω=∞ |
| jQ(ω) |
| ω=1/T |
| ω=0 |
| P(ω) |
| k |

Аналізуючи графік функції  , видно, що гармонійні сигнали малої частоти (
, видно, що гармонійні сигнали малої частоти (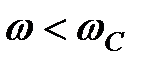 ) пропускаються ланкою добре - з відношенням амплітуд вихідної і вхідної величин, близьким до передавального коефіцієнта k. Сигнали великої частоти (
) пропускаються ланкою добре - з відношенням амплітуд вихідної і вхідної величин, близьким до передавального коефіцієнта k. Сигнали великої частоти ( ) погано пропускаються ланкою: відношення амплітуд істотно менше коефіцієнта k. Чим більше постійна часу Т, тобто чим більше інерційність ланки, тим менше АЧХ витягнута уздовж осі частот, або, як прийнято говорити в ТАУ, тим вужче смуга пропускання частот. Таким чином, інерційна ланка першого порядку по своїх частотних властивостях є фільтром низької частоти.
) погано пропускаються ланкою: відношення амплітуд істотно менше коефіцієнта k. Чим більше постійна часу Т, тобто чим більше інерційність ланки, тим менше АЧХ витягнута уздовж осі частот, або, як прийнято говорити в ТАУ, тим вужче смуга пропускання частот. Таким чином, інерційна ланка першого порядку по своїх частотних властивостях є фільтром низької частоти.


ФЧХ: 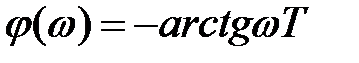
|
ВЧХ: 
|
| L(ω) |
| 20lgk |
| lgωc |
| -20дБ/дek |
| lgω |

МЧХ: 
|
ЛАЧХ: 
|
У практичних розрахунках використовують наближену або асимптотичну характеристику  , яка є ламана у вигляді двох асимптот.
, яка є ламана у вигляді двох асимптот.
Першу асимптоту (низькочастотна) маємо при низьких частотах, коли величиною  у виразі
у виразі  можна нехтувати і прийняти, що
можна нехтувати і прийняти, що  . Низькочастотна асимптота від частоти не залежить і є прямою, паралельною осі частот і віддалену від неї на відстані
. Низькочастотна асимптота від частоти не залежить і є прямою, паралельною осі частот і віддалену від неї на відстані  .
.
Друга асимптота (високочастотна) замінює точну характеристику при великих частотах, коли 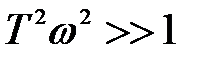 , і одиницю під коренем у виразі
, і одиницю під коренем у виразі  можна не враховувати. Вираз для цієї асимптоти має вигляд:
можна не враховувати. Вираз для цієї асимптоти має вигляд:  .
.
Ця асимптота залежить від частоти. У логарифмічній системі координат вона є прямою, що має негативний нахил і що проходить через точку з координатами  ,
,  . Приріст високочастотної асимптоти, що приходить на одну декаду, рівний -20 дб.
. Приріст високочастотної асимптоти, що приходить на одну декаду, рівний -20 дб.
Значення сполучної частоти  при якій перетинаються обидві асимптоти, знайдемо з умови
при якій перетинаються обидві асимптоти, знайдемо з умови  , звідки
, звідки 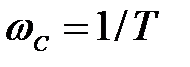 .
.
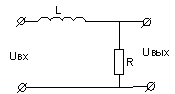 Інерційними ланками першого порядку є конструктивні елементи, які можуть накопичувати і передавати енергію або речовину. У електричних елементах накопичувачем енергії електричного поля служить конденсатор, а магнітного поля - індуктивність. У механічних елементах потенційна енергія накопичується в пружинах і інших пружних елементах, а кінетична - в рухомих масах.
Інерційними ланками першого порядку є конструктивні елементи, які можуть накопичувати і передавати енергію або речовину. У електричних елементах накопичувачем енергії електричного поля служить конденсатор, а магнітного поля - індуктивність. У механічних елементах потенційна енергія накопичується в пружинах і інших пружних елементах, а кінетична - в рухомих масах.

k = 1 T = RC k = 1 T = L/R
Інтегруючі ланки
Розрізняють два види інтегруючих ланок: ідеальні і реальні. Загальною особливістю інтегруючих ланок є пропорційність похідної вихідної величини миттєвому значенню вхідної величини. Причому, у ідеальної інтегруючої ланки пропорційність існує у будь-який момент часу після подачі стрибкоподібного сигналу, а у реального - тільки після завершення перехідного процесу.
(1) Ідеальна інтегруюча ланка:  ,
,  , T – постійна часу ідеального інтегратора.
, T – постійна часу ідеального інтегратора.
(2) Реальна інтегруюча ланка: 
- ПФ ідеальне:  , реальне
, реальне 


ідеальне (1) 
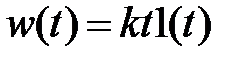
реальне (2) 
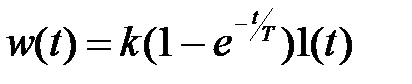
Перехідна функція ідеального інтегратора лінійно зростає з часом. Швидкість росту зворотно пропорційна постійною часу інтегратора. Вихідний сигнал інтегратора досягає рівня стрибкоподібної функції за час, що дорівнює постійній часу Т інтегратора.
(1) 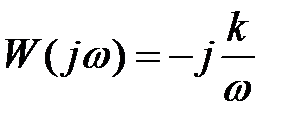 (2)
(2) 
|


(1)  (1)
(1) 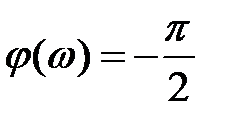
(2)  (2)
(2) 
(1)  (2)
(2) 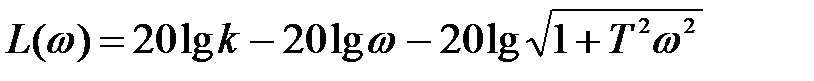
|

Інтегруючі властивості властиві всім об'єктам керування, в яких відбувається накопичення речовини або енергії без її одночасної віддачі в навколишнє середовище. Класичним прикладом об'єкту з інтегруючими властивостями є резервуар з рідиною (рис. 3.13, а), якщо в якості вхідноі змінної розглядати подачу рідини Q (м3/с), а вихідної - рівень рідини h (м).
Інтегруючими ланками є також різні виконавчі двигуни і механізми - пристрої, які переміщають регулюючі органи (шибери, заслінки, вентилі і т. д.).
Загальні властивості і особливості інтегруючих ланок:
1.Після подачі стрибкоподібного вхідного впливу 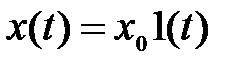 вихідна змінна у(t) необмежено зростає і після закінчення перехідного процесу змінюється по лінійному закону
вихідна змінна у(t) необмежено зростає і після закінчення перехідного процесу змінюється по лінійному закону  .
.
При знятті вхідного впливу вихідна змінна зберігає досягнуте значення, тому інтегруючі ланки можна використовувати як елементи, що запам'ятовують (елементів з пам'яттю).
2. У передавальну функцію обов'язково входить співмножник 1/p, тому  , а
, а  .
.
3. Інтегруючі ланки, є фільтрами низької частоти; у режимі гармонійного коливання вони вносять від’ємні фазові зсуви.
Диференцюючі ланки
Бувають ідеальними (безінерційними) і реальними (інерційними). Миттєве значення вихідної величини ідеальної диференціальної ланки пропорційне в кожен момент часу першої похідної від вхідної величини:


W(p) = kp; 

|
| T |
| h(t) |
1) 

1)  1)
1) 
| φ(ω) |
| 900 |
| 450 |
| ω |
| ωc=1/T |
 2)
2) 
1) 

2) 
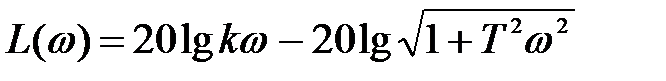
Загальні властивості і особливості диференцюючих ланок:
1. При подачі на вхід ланки стрибкоподібного впливу на його виході виникає великий короткочасний імпульс, а потім після закінчення перехідного процесу вихідна змінна стає рівною нулю. Якщо вхідний сигнал не змінюється в часі, то вихідний дорівнює нулю.
2. У передавальну функцію завжди входить співмножник p, тому W(p)|p=0=0, і диференцюючі ланки в статиці не передають вхідні сигнали.
3. Диференцюючі ланки є фільтрами високої частоти, тобто добре пропускають високочастотні сигнали і погано - низькочастотні.






