Автоматична система управління, що описується характеристичним рівнянням
стійка, якщо при a0 > 0 позитивні всі визначники D1, D2,…, Dn виду
, i = 1, 2, 3, …, n.
Якщо хоч би один з визначників, які називають визначниками Гурвіца, негативний, то система нестійка.
Визначники Гурвіца складають таким чином: на головній діагоналі записують всі коефіцієнти характеристичного рівняння від a1 до ai (в порядку зростання індексу), потім в кожному стовпці вище за діагональні елементи записують коефіцієнти з послідовно зростаючими індексами, а нижче - з послідовно убуваючими індексами; на місце з коефіцієнтами з індексами більшими за n або меншими нуля проставляють нулі. При цьому кожен i-й визначник виходить розміром i ´ i.
Якщо головний визначник дорівнює нулю ∆n = 0, а решта всіх визначників позитивна, то система знаходиться на межі стійкості.
Оскільки останній стовпець головного визначника ∆n містить завжди тільки один елемент an, відмінний від нуля, то згідно відомій властивості визначників: ∆n = an*∆n-1.
Умова ∆n = 0 розпадається на два: an = 0 або ∆n-1 = 0.
Умова an = 0 відповідає один нульовий корінь, тобто аперіодична межа стійкості, а умові ∆n-1 = 0 – пара уявних коренів, тобто коливальна межа стійкості.
Критерій стійкості Рауса.
Його доцільно застосовувати для систем вище за четвертий порядок. Для цього складають таблицю з коефіцієнтів характеристичного рівняння:
.
У першому рядку таблиці (i = 1) записують коефіцієнти рівняння з парними індексами, в другому рядку (i = 2) – коефіцієнти з непарними індексами, в подальших рядках (i ³ 3) розміщені коефіцієнти Рауса, отримані в результаті ділень різниці перехресних перемножень коефіцієнтів двох попередніх рядків на коефіцієнт першого стовпця попереднього рядка:
де i – номер рядка, k – номер стовпця.
Система автоматичного керування стійка, якщо є позитивними коефіцієнти першого стовпця таблиці Рауса, включаючи а0 і а1.
Якщо не всі коефіцієнти стовпця позитивні, то система нестійка. При цьому число змін знаку серед цих коефіцієнтів відповідає числу правих коренів характеристичного рівняння.
| Рядок | Стовпець | |||||
| … | ||||||
| r11 = a0 | r12 = a2 | r13 = a4 | r14 = a6 | … | … | |
| r21 = a1 | r22 = a3 | r23 = a5 | r24 = a7 | … | … | |
| 
| 
| 
| … | … | |
| 
| 
| … | … | … | |
| 
| … | … | … | … | |
| ... | … | … | … | … | … | … |
| n+1 | … | … | … | … | … | … |
Критерій Михайлова.
Критерій Михайлова, як і критерій Гурвіца і Рауса, заснований на аналізі характеристичного рівняння системи, тому з його допомогою можна судити про стійкість замкнутих і розімкнених систем.
Ліва частина характеристичного рівняння називається характеристичним поліномом і має вигляд:
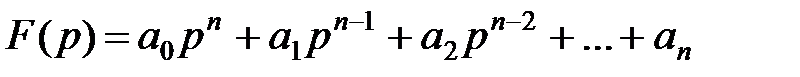
Підставивши в цей поліном замість змінної p чисто уявний корінь jw: p®jw отримаємо функцію комплексної змінної:
F(jw) = а0(jw)n + а1(jw)n-1 + а2(jw)n-2 +…+ an.
Функцію F(jw) можна представити у вигляді суми дійсної і уявної частини: F(jw) = P(w)+jQ(w).
Дійсна частина P(w) містить тільки парні ступені w:
P(w) = an – an-2w2 + an-4w4 - …
Уявна частина містить тільки непарні ступені:
Q(w) = an-1w – an-3w3 + …
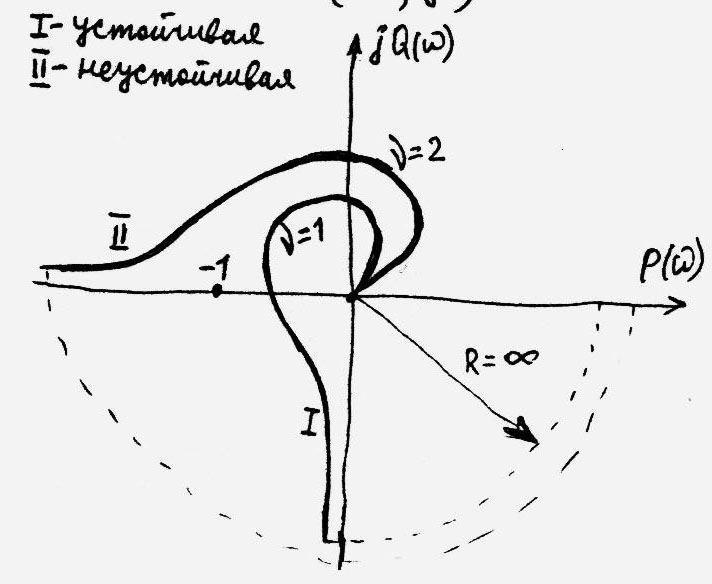
Кожному значенню w відповідає комплексне число, яке може бути зображено у вигляді вектора на комплексній площині. Якщо тепер змінювати w від 0 до ¥, то кінець вектора F(jw) опише деяку криву, яка називається характеристичною кривою або годографом Міхайлова.
Критерій Міхайлова:
Автоматична система управління, що описується рівнянням n-го порядку, стійка, якщо при зміні w от 0 до ¥ характеристичний вектор системи F(jw) обернеться проти годинникової стрілки на кут 
, не звертаючись при цьому в нуль. Це означає, що характеристична крива стійкої системи винна при зміні w від 0 до ¥ пройти послідовно n чвертей.
Крива F(jw) завжди починається в точці на дійсній осі, віддаленій в позитивному напрямі від початку координат на величину an. Характеристичні криві, що відповідають стійким системам, мають плавну спіралеподібну форму і йдуть в нескінченність в тій чверті, номер якої дорівнює порядку характеристичного рівняння. Якщо характеристична крива проходить n чвертей непослідовно, або проходить менше число чвертей, то система нестійка.
Якщо крива F(jw) проходить через початок координат, то система знаходиться на межі стійкості. Якщо F(jw)= 0 при w = 0 - аперіодична межа стійкості; якщо F(jw)= 0 при w ≠ 0 - коливальна межа.
Визначення типу межі стійкості по вигляду годографа Міхайлова
1. Астатизм першого порядку - "аперіодична" межа стійкості.
2. Астатизм другого порядку - "аперіодична" межа стійкості.
3. "Коливальна" межа стійкості.
4. Межа стійкості типу "нескінченний корінь".
Слідство з критерію Міхайлова:
Система стійка, якщо дійсна і уявна частини характеристичної функції F(jw) звертаються в нуль по черзі, тобто корені рівнянь Р(w) =0 і Q(w) =0 перемежаються.
Критерій Найквіста
Основні переваги критерію Найквіста:
1. Основна відмінність і гідність даного критерію від критеріїв Гурвіца, Рауса і Міхайлова в тому, що критерій Найквіста дозволяє судити про стійкість замкнутої системи по амплитудно-фазовій характеристиці розімкненого контура системи.
2. Критерій застосовується в тих випадках, коли диференціальні рівняння системи або окремих її ланок невідомі, але відомі частотні характеристики, отримані, наприклад, експериментально.
3. Використання критерію не так різко ускладнюється при збільшенні порядку характеристичного рівняння, як це має місце при застосуванні алгебраічних критеріїв.
4. Критерій Найквіста ще в більшому ступені, чим критерій Гурвіца, дозволяє безпосередньо встановити вплив на стійкість системи різних її ланок.
5. Критерій дає уявлення про ступінь стійкості системи і показує можливі шляхи її поліпшення, якщо в цьому є необхідність.
6. Критерій дозволяє пов'язати дослідження стійкості з подальшим аналізом якості як в сталому, так і в перехідному режимах.
При аналізі стійкості системи по критерію Найквіста можна виділити три випадки:
- система в розімкненому стані стійка;
- система в розімкненому стані нейтральна;
- система в розімкненому стані нестійка.
1. Система в розімкненому стані стійка
Автоматична система керування стійка, якщо АФЧХ W(jw) розімкненого контуру не охоплює точку з координатами (-1; j0).
| На рисунку: 1 - стійка система; 2 - система на коливальній межі стійкості; 3 - нестійка система. |
Поняття обхвату точки має деяку невизначеність, із-за чого у випадках складної форми кривої W(jw) можуть виникати ускладнення в розсудках про стійкість системи. Тому застосовується наступний прийом. Треба в думках простежити за рухом вектора W1(jw) = 1+W(jw), що обертається навколо точки (-1; j0) і що ковзає по кривій W(jw). Кут повороту вектора W1(jw) рівний p, означає обхват крапки (-1; j0), а кут менший p, - не обхват.
Для вирішення питання про стійкість систем, АФЧХ складної конфігурації, у котрих крива АФЧХ перетинає дійсну вісь лівіше за крапку (-1; j0) кілька разів, можна використовувати правило переходів:
АФЧХ не охоплює крапку (-1; j0), тобто система стійка, якщо при зростанні w різниця між числом позитивних (зверху вниз) і негативних (від низу до верху) переходів АФЧХ через вісь абсцис зліва від крапки (-1; j0) дорівнює нулю.
2. Система в розімкненому стані нейтральна
| Якщо система в розімкненому стані нейтральна, то для стійкості системи в замкнутому стані необхідно і достатньо щоб АФЧХ розімкненої системи W(jw), разом з доповненням її дугою нескінченно-великого радіусу, що починається на позитивному напрямі дійсної осі, не охоплювала крапку з координатами (-1; j0). |
Приклади годографів Найквіста астатичних САУ
1. Стійка САР з астатизмом першого порядку.
2. Стійка САР з астатизмом другого порядку.
3. Стійка САР з астатизмом третього порядку.
4. Нестійка САР з консервативною ланкою.
5. Стійка САР з консервативною ланкою (корекція виконана фазообертаючою ланкою).
Фізичне трактування критерію Найквіста
Вводять два поняття:
- частота, при якій АЧХ A(w) = | W(jw) | = 1 частота зрізу wср;
- частота, при якій ФЧХ j(w) = - p, позначають wp.
Умова знаходження системи на межі стійкості: wср = wp
На вході системи діє гармонічний сигнал g(t)=gmsinwt з малою амплітудою gm. Хай частота w дорівнює частоті wp при якій фазове зрушення j(w), створюваний ланкою W(jw) рівний -p. Тоді сигнал негативного зворотного зв'язку опиниться у фазі з сигналом g(t), і миттєві значення сигналів підсумовуватимуться.
Якщо на частоті w = wp модуль |W(jwp)| = 1, тобто wср = wp, то в контурі системи будуть незгасаючі коливання навіть після зникнення зовнішнього впливу g(t). Система знаходиться на межі стійкості, характеристика W(jw) проходить через точку (-1; j0).
Якщо на частоті w = wp модуль |W(jwp)| < 1, то після зникнення зовнішнього впливу коливання в контурі затухнуть. Система стійка, характеристика не охоплює точку (-1; j0).
Якщо на частоті w = wp модуль |W(jwp)| >1, то амплітуда сигналів в контурі необмежено зростатиме. Система нестійка, характеристика W(jw) охоплюватиме точку (-1; j0).
Особлива роль точки (-1; j0) – по-перше, в цій точці НЗЗ перетворюється на ПЗЗ; по-друге - є граничною між режимами ослаблення і посилення сигналів ланкою W(jw).
3. Система в розімкненому стані нестійка.
Автоматична система управління стійка якщо АФЧХ W(jw) розімкненого контуру охоплює l/2– раз точку з координатами (-1; j0), де l - число правих коренів характеристичного рівняння розімкненого контуру.
Іншими словами, лівіше за точку (-1; j0) різниця між числом позитивних і числом негативних переходів АФЧХ через вісь абсцис повинно дорівнювати l/2.
Кількість обхватів при цьому можна визначати за вище розглянутим правилом, як різниця між числом позитивних і негативних переходів.
Логарифмічний критерій стійкості Найквіста
Система стійка, якщо при досягні ФЧХ значення -π ЛАЧХ буде негативною: wср < wp - система стійка;
wср = wp - система на межі стійкості;
wср > wp - система нестійка.
| Система стійка, якщо різниця між позитивними і негативними переходами ФЧХ лінії (-p) у інтервалі частот від 0 до wср дорівнює нулю (ФЧХ повинна перетинати рівень (-p) у інтервалі частот від 0 до wср парне число разів). |
Якщо розімкнений ланцюг нестійкий і має l правих коренів, то використовують наступне формулювання логарифмічного критерію Найквіста:
Система стійка, якщо різниця між позитивними і негативними переходами ФЧХ лінії (-p) у інтервалі частот від 0 до wср дорівнює l/2.
