Денежки счет любят
(Как Вы уже поняли, геодезия – тоже)
135.1. Способ матричных преобразований
В качестве примера рассмотрим решение системы четырех линейных уравнений матричным способом:
1. 4 х1 – 2 х2 + 3 х3 – 2 х4 = +1;
2. - 2 х1 + 5 х2 – 2 х3 + х4 = + 6; (14.53)
3. 3 х1 – 2 х2 + 3 х3 – 4 х4 = - 8;
4. - 2 х1 + х2 –4 х3 + 2 х4 = - 4.
Составим матрицу коэффициентов при хi, правых частей и контрольного столбца, равного суммам коэффициентов и правой части каждого уравнения по соответствующй строке матрицы:
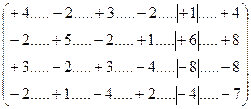(14.54)
Составление контрольного столбца является обязательным! После математических действий с полной строкой, включая и контрольный столбец, всегда следует выполнять проверку сумм коэффициентов уравнений правой и левой частей с полученным новым значением контрольного столбца. Они должны совпадать в пределах округлений результатов. Если этого не делать, то погрешность в вычислениях выявится только после решения систем уравнений. А процесс этот довольно трудоемкий, и без постоянного контроля вся работа может оказаться напрасной.
Из математики известно, что результат решения не изменится, если:
- любую строку матрицы поменять местами с другой строкой;
- любую строку матрицы умножить или разделить на одно и то же постоянное число.
Решение матрицы сводится к образованию т.н. треугольной матрицы вида
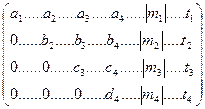. (14.55)
Таким образом получается система линейных уравнений
a1k1 + a2k2 + a3k3 + a4k4 = m1
b2k2 + b3k3 + b4k4 = m2 (14.56)
c3k3 + c4k4 = m3
d4k4 = m4
для, например, четырех линейных уравнений. Из последней строки находят значение k4:
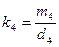(14.57)
и последовательной подстановкой в уравнения (14.56) решают задачу.
Контроль решения осуществляется подстановкой полученных значений k в исходные уравнения (14.53).
Проследим решение на приведенном примере.
Шаг 1. Образовать 1-й нулевой столбец в строках 2, 3 и 4 матрицы (14.54). Для этого умножим 2-ю и 4-ю строки на (+2), а 3-ю строку – на (-4/3). Получим:
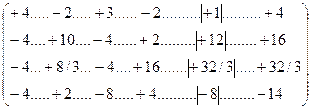. (14.58)
Затем последовательно сложим 2-ю, 3-ю и 4-ю строки (14.58) с первой строкой этой матрицы:
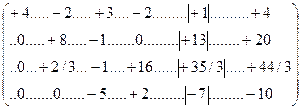. (14.59)
Шаг 2. Образовать 2-й нулевой столбец в строках 3 и 4 (14.59). При этом в примере для строки 4 нет необходимости в преобразованиях, поскольку в ней на второй позиции уже имеется ноль. В связи с этим достаточно преобразовать только 3-ю строку. Для этого умножим ее на (-12)
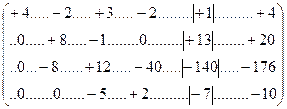(14.60)
и сложим полученную строку со 2-й строкой той же матрицы:
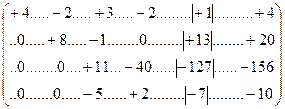. (14.61)
Шаг 3. Образовать нулевой 3-й столбец (14.61) в строке 4, для чего требуется умножить его на (+2,2)
(14.62)
и сложить со строкой 3 этой же матрицы (14.62):
(14.63)
В результате система линейных уравнений (14.53) преобразуется к виду:
1. +4 k1 – 2 k2 + 3 k3 - 2 k4 = + 1;
2. +8 k2 - k3 = + 13;
3. +11 k3 - 40 k4 = - 127; (14.64)
4. – 35,6 k4 = - 142,4.
Из уравнения 4 (14.64) находим k4 = +4. Из уравнения 3 подстановкой в него значения k4 находим k3 = +3. Из уравнения 2 подстановкой k3 (коэффициент при k4 равен нулю) находим k2 = +2. Из уравнения 1, после подстановки значений k2, k3 и k4, находим k1 = +1.
В качестве замечаний к решению систем линейных уравнений необходимо указать следующее. При уравнивании значения коэффициентов и свободных членов системы линейных уравнений часто являются не целыми числами, а дробными. В связи с этим рекомендуется величины весов и обратных весов округлять до 0,01 – 0,001 ед., значения коэффициентов при неизвестных округлять до 0,0001ед., получаемые значения неизвестных округлять до 0,001 – 0,0001 ед. При этом, как указывалось выше, поправки в углы часто округляют до 0,1" – 0,01", в расстояния (приращения координат) – до 1 мм, в превышения – до 0,1 – 1,0 мм.
135.2. Решение систем линейных уравнений по алгоритму Гаусса
В основе алгоритма Гаусса лежит метод последовательного исключения неизвестных, рассмотренный выше. Алгоритм весьма прост вследствие простых однотипных действий на каждом последующем шаге вычислений. При этом обеспечивается надежный контроль промежуточных результатов. Кроме того, алгоритм Гаусса упрощает решение систем линейных уравнений при введении в них дополнительных граф, необходимых для вычисления весов уравненных элементов или их функций (об этом будет сказано позже).
Алгоритм Гаусса рассмотрим на примере системы четырех линейных уравнений вида:
;
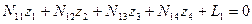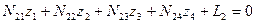; (14.65)
;
.
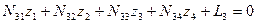Укажем, что в этой системе линейных уравнений, составленных при решении задачи уравнивания, коэффициенты с одинаковыми двойными индексами являются квадратичными (диагональными). Диагональные коэффициенты по условию их получения при составлении условных линейных уравнений всегда положительные. Коэффициенты, имеющие обратные индексы, равны между собой. В связи с симметрией коэффициентов относительно диагональных таблицу коэффициентов обычно записывают сокращенно в таком виде:
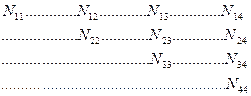, (14.66)
имея в виду наличие и симметричных коэффициентов на незаполненных местах.
Составим т.н. элинимационное уравнение, которое в алгоритме Гаусса обозначают буквой Е. Это уравнение представляет собой выражение первого неизвестного z 1 через остальные (уравнение Е1):
. (14.67)
Подставим в уравнения (14.65) полученное значение z 1 и запишем новую систему линейных уравнений без неизвестного z 1:
;
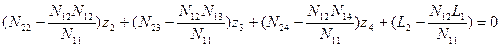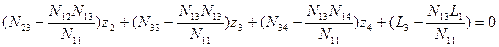; (14.68)
.
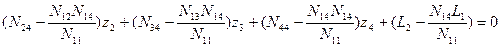Введем следующие обозначения:
; 
; 
;
; 
; 
;
; 
; 
.
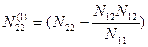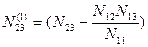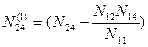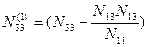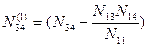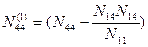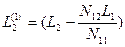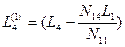Для полученных коэффициентов сохраняются все особенности системы линейных уравнений с диагональными коэффициентами, имеющими одинаковые двойные индексы (22, 33, 44 и т.д., если уравнений более 4-х). Таким образом, можно записать преобразованную систему линейных уравнений:
;
; (14.69)
.
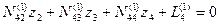Составим второе элинимационное уравнение Е2:
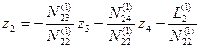. (14.70)
Подставим значение z 2 в уравнения (14.69):
;
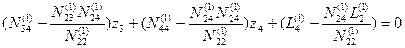. (14.71)
Снова введем обозначения:
; 
; 
;
; 
.
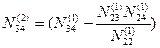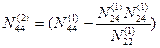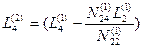В результате получим систему линейных уравнений с двумя неизвестными:
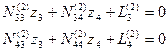(14.72)
Третье элинимационное уравнение (Е3) в этом случае имеет вид:
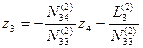(14.73)
Подставим значение z 3 в уравнения (14.72), получим
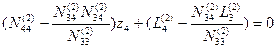. (14.74)
Введя в уравнение (14.74) соответствующие обозначения, как и в предыдущих случаях, получим окончательное уравнение с одним неизвестным в обозначениях Гаусса:
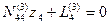. (14.75)
Из уравнения (14.75) найдем
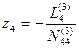. (14.76)
Затем, для определения остальных неизвестных, воспользуемся последовательно элинимационными уравнениями Е3, Е2 и Е1, в результате чего получим значения z 3, z 2 и z 1.
Обратим внимание на то, что для определения неизвестных нужны только элинимационные уравнения. Остальные уравнения не используются.
Представим схему решения системы четырех линейных уравнений в виде таблицы Гаусса (табл. 14.1).
Запись коэффициентов N в строке (3), (7), (12) сокращенная, только вправо от диагональных коэффициентов. Но контрольная сумма этой строки учитывает все коэффициенты, стоящие слева от диагонального. В первой строке записываются все коэффициенты.
После заполнения с вычислениями и контролем строк (1), (2), (3) и (4), что не требует пояснений, заполняют строку (5). Коэффициенты в этой строке равны сумме (3) и (4) строк по столбцам. По аналогии со строкой (2) получают коэффициенты второго элинимационного уравнения Е2. В строку (7) заносят в сокращенном виде коэффициенты и свободный(ые) члены третьего нормального уравнения. После вычисления строк (8) и (9) по суммам в столбцах строк (7), (8) и (9) получают коэффициенты строки (10). Все дальнейшие действия аналогичны приведенным выше до вычисления коэффициентов в данном случае последнего элинимационного уравнения Е4. Коэффициент N 55 представляет собой указанную в строке (18) сумму произведений весов на квадраты свободных членов. При суммировании столбца по значениям строк (18) – (22) получают значение N 55(4) = [ pv 2].
Значения неизвестных zi получают с помощью элинимационных уравнений:
;
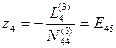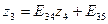; (14.77)
;
.
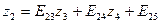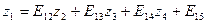Рассмотрим пример решения системы линейных уравнений по алгоритму Гаусса. Для этого решим систему уравнений (14.53)
1. 4 х1 – 2 х2 + 3 х3 – 2 х4 – 1 = 0;
2. - 2 х1 + 5 х2 – 2 х3 + х4 – 6 = 0;
3. 3 х1 – 2 х2 + 3 х3 – 4 х4 + 8 = 0;
4. - 2 х1 + х2 –4 х3 + 2 х4 + 4 = 0.
Решение уравнений выполним по приведенному выше алгоритму в табл. 14.2.
В табл. 14.2 приведен только пример вычисления неизвестных х без оценки точности (указанные примеры будут рассмотрены отдельно).
Таблица 14.1
Алгоритм Гаусса решения систем линейных уравнений
| №№ п/п | Дейст-вия | z1 | z2 | z3 | z4 | L | ∑ |
| N1 | N11 | N12 | N13 | N14 | L1 | ∑1 | |
| Е1 | - 1 |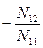 
| 
| 
| 
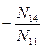
| ∑E1 | |
| N2 | N 22 | N 23 | N 24 | L 2 | ∑2 | ||
| E12 N | E12 N 12 | E12 N 13 | E12 N 14 | E12 L 1 | E12∑1 | ||
| N2(1) | N 22(1) | N 23(1) | N 24(1) | L 2(1) | ∑N2(1) | ||
| E2 | - 1 |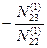 
| 
| 
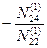
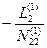
| ∑E2 | ||
| N3 | N 33 | N 34 | L 3 | ∑3 | |||
| E13 N | E13 N 13 | E13 N 14 | E13 L 1 | E13∑1 | |||
| E23 N (1) | E23 N 23(1) | E23 N 24(1) | E23 L 2(1) | E23∑N2(1) | |||
| N3(2) | N 33(2) | N 34(2) | L 3(2) | ∑N3(2) | |||
| E3 | - 1 | 
| 
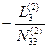
| ∑E3 | |||
| N4 | N 44 | L 4 | ∑4 | ||||
| E14 N | E14 N 14 | E14 L 1 | E14∑1 | ||||
| E24 N (1) | E24 N 24(1) | E24 L 2(1) | E24∑N2(1) | ||||
| E34 N (2) | E34 N 34(2) | E34 L 3(2) | E34∑N3(2) | ||||
| N4(3) | N 44(3) | L 4(3) | ∑N4(3) | ||||
| E4 | - 1 |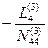 
| ∑E4 | ||||
| N5 | [ pll ] | ∑5 | |||||
| E15 N | E15 L 1 | E15∑1 | |||||
| E25 N (1) | E25 L2 (1) | E25∑N2(1) | |||||
| E35 N (2) | E35 L3 (2) | E35∑N3(2) | |||||
| E45 N (3) | E45 L4 (3) | E45∑N4(3) | |||||
| N 5(4) | N 55(4) | ≈ [ pv2 ] |
Таким образом, значение х 4 = Е45 = +3,999 ≈ +4.
х 3 = +3,639 ∙ (+3,999) – 11,553 = +2,999 ≈ +3.
х 2 = +0,125 ∙ (+2,999) + 0 + 1,625 = +2.
х 1 = +0,5 ∙ (+2) – 0,75 ∙ (+3) + 0,5 ∙ (+4) + 0,25 = +1.
Получены такие же ответы, как и в способе матричных преобразований.
Незначительные отклонения от значений вызваны необходимостью округления промежуточных результатов вычислений.
Таблица 14.2
Решение системы линейных уравнений (14.53) по алгоритму Гаусса
| №№ п/п | Дейст-вия | х1 | х2 | х3 | х4 | L | ∑ |
| N1 | +4 | -2 | +3 | -2 | -1 | +2 | |
| Е1 | -1 | +0,5 | -0,75 | +0,5 | +0,25 | -0,5 (-0,5) | |
| N2 | +5 | -2 | +1 | -6 | -4 | ||
| E12 N | -1 | +1,5 | -1 | -0,5 | +1,0 (+1,0) | ||
| N2(1) | +4 | -0,5 | -6,5 | -3 | |||
| E2 | -1 | +0,125 | +1,625 | +0,75 | |||
| N3 | +3 | -4 | +8 | +8 | |||
| E13 N | -2,25 | +1,5 | +0,75 | -1,5 (-1,5) | |||
| E23 N (1) | -0,063 | -0,813 | -0,375 | ||||
| N3(2) | +0,687 | -2,5 | +7,937 | +6,125(+6,124) | |||
| E3 | -1 | +3,639 | -11,553 | -8,916 | |||
| N4 | +2 | +4 | +1 | ||||
| E14 N | -1 | -0,5 | +1 | ||||
| E24 N (1) | |||||||
| E34 N (2) | -9,098 | +28,883 | +22,289(+22,285) | ||||
| N4(3) | -8,098 | +32,383 | +24,289(+24,285) | ||||
| E4 | -1 | +3,999 | +2,999 |
