Под методикой инженерно-геодезических измерений понимается полная и последовательная совокупность действий, соблюдение которых при измерениях и обработке данных позволяет обеспечить необходимую (заданную) точность измерений.
В связи с этим в понятие «методика» входят требования ко всем элементам, участвующим в измерениях: к опытности наблюдателя; типу используемых приборов; к конструкциям геодезических знаков (исходных и рабочих); к условиям производства работ; к способам обработки результатов измерений и мн.др.
Все указанные требования определяются, в первую очередь, качественной характеристикой схемы измерений. Качественным показателем для каждого элемента схемы измерений является единица веса либо вес р данного элемента (или обратный вес q=1/р данного элемента). Элементом схемы измерений может явиться отдельная её точка, секция (ход между двумя точками), полигон и т.п.
Указанные в техническом задании требования к точности измерений относятся ко всем точкам системы, независимо от их расположения на объекте, а также независимо от используемой схемы измерений. В связи с этим, для выбора класса измерений необходимо определить качественную характеристику для самой слабой точки Е схемы измерений. То есть для точки в схеме измерений, погрешность определения координат которой будет наибольшей. При этом очевидно, что для остальных точек схемы обеспечение необходимой точности измерений будет реализовано.
Рассмотрим пример определения качественных характеристик схемы измерений на основе измерения вертикальных перемещений двух зданий (рис. 13.9 а).
На здании 7КЖ запроектировано наблюдение 14 точек, причем, точки 5, 6 и 8, 9 – двойные, находятся в местах стыка конструкций здания. На здании 2К размещено 4 точки. Привязка выполнена к исходному реперу R. На рис. 13.9 б показана запроектированная схема нивелирных ходов, проложенных с учетом условий измерений. На схеме нивелирных ходов указаны качественные характеристики превышений в секциях (обратные веса превышений), определяемые числом штативов (станций), необходимых для измерения данного превышения. Так, q = 1 – одна станция, q = 2 – две станции. То есть единицей веса здесь, например, является превышение, измеренное в ходе одного направления при одном горизонте прибора по двум шкалам нивелирной рейки на одной станции, а также с учётом примерного равенства плеч на станциях.
Для определения наиболее слабой точки в приведённой схеме измерений (точки, имеющей наибольшее значение q), необходимо выполнить преобразования (эквивалентную замену) до установления непосредственной связи исходного репера (исходных реперов) со слабоопределяемой точкой. Схемы возможных преобразований представлены на рис. 13.10.
Рис. 13.9. Схема измерения вертикальных перемещений:
а) размещение рабочих реперов на сооружениях; б) схема нивелирных ходов.
Рис. 13.10. Преобразования схем способом эквивалентной замены:
а) в полигоне; б) между узловыми точками; в) для точки, находящейся в секции между исходными пунктами; г) преобразование «треугольник-звезда»; д) преобразование «звезда-треугольник».
Для любой точки А полигона (рис. 13.10 а), включающего исходный репер либо опирающегося на узловую точку, значение качественной характеристики qА определяется по формуле
. (13.6)
В частности, если q1=q2=q, т.е. точка А находится по весовым характеристикам посредине полигона (является наиболее слабой точкой Е), то
, (13.7)
где П – периметр полигона (
).
Если замкнутый полигон имеет две узловые точки (рис. 13.10 б), то значение качественной характеристики q1-2 определяется также по формуле (13.6). По той же формуле (13.6) определяется и качественная характеристика эквивалентной секции R-A (рис. 13.10 в). В этом случае полагают ничтожное влияние погрешностей исходных данных того и другого реперов и объединяют их в один, т.е. образуют схему рис. 13.10 а.
При преобразованиях «треугольник-звезда» (рис. 13.10 г) образуется условная точка Х (узловая точка), относительно которой получают качественные характеристики для соответствующих условных секций:
; 
; 
, (13.8)
где П1 = q1 + q2 + q3 – периметр треугольника.
При преобразованиях «звезда-треугольник» (рис. 13.10 д) условными секциями являются стороны образовавшегося треугольника с их качественными характеристиками:
; 
; 
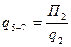, (13.9)
где П2 = q1 ∙ q2 + q3 ∙ q1 + q2 ∙ q3.
Обратите внимание на то, что при преобразованиях «звезда-треугольник» исключается узловая точка 4.
Решим теперь задачу поиска наиболее слабой точки Е системы нивелирных ходов (рис. 13.9) и её качественной характеристики qЕ. Здесь логично предположить, что указанная точка Е находится в секции 10-18. При затруднениях в поисках слабой точки задача решается подбором для нескольких точек по нескольким вероятным направлениям до получения максимального значения qЕ.
Предварительно выделим замкнутый контур А (рис. 13.11) и выполним в нем преобразование «треугольник-звезда». При этом секция 3-1 будет иметь качественную характеристику 
.
Используя формулы (13.8), найдем качественные характеристики получившихся секций звезды:
;
;
.
С учетом полученных значений q, а также схемы нивелирных ходов, составим новую схему (рис. 13.12 а – сплошные линии), в которой образуем секции между узловыми точками:
;
;
;
.
Далее выполним преобразования «треугольник-звезда» в двух треугольниках (R10Х1 и R18Х1). В результате получим схему рис. 13.12 б. В этой схеме из треугольника RХ2Х3 образуем звезду с узловой точкой Х4. В результате получим схему рис. 13.12 в, которая состоит из секции RX4 и замкнутого полигона, включающего слабую точку Е в ходе Х4-Х2-10-11-12-13-14-15-16-17-18-Х3-Х4. Периметр этого полигона составит:
.
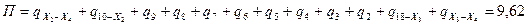Рис. 13.12. Преобразование схемы нивелирных ходов.
С учетом формулы (13.7) 
, а качественная характеристика слабой точки Е, с учетом 
, составит при этом 2,52 (рис. 13.12 г).
Требования к точности измерения превышений между отдельными точками в секциях по принятому ходу определяются выражением:
, (13.10)
где mh – требуемая средняя квадратическая погрешность измерения превышений; M Δ – требуемая точность измерения деформации отдельной точки; qE – качественная характеристика слабой точки схемы.
Так, для рассматриваемого примера, полагая значение M Δ = 1 мм, получим mh = 0,45 мм.
На основании полученного значения mh производят выбор необходимых технических средств, проектируют (уточняют) схемы измерений, устанавливают методику измерения превышений на станции и т.д.
