Параметрический способ уравнивания

 

При уравнивании сложных по построению геодезических сетей, в которых имеется обычно большое число избыточных измерений, применение коррелатного способа является практически менее выгодным. Это связано с тем, что в сложных сетях образуется сравнительно большое число геометрических условий (см. § 134), т.е. возникает необходимость решения значительного числа нормальных уравнений. При уравнивании сложных геодезических сетей предпочтение отдают параметрическому способу. В данном случае его рекомендуется применять практически для любых построений: обширных геодезических сетей триангуляции и трилатерации, для весьма сложных фигур триангуляции 3 и 4 классов, в схемах различных линейно-угловых построений и др.

Чаще всего при уравнивании плановых геодезических построений параметрическим способом в качестве неизвестных величин (или необходимых параметров t_j) выбирают координаты определяемых пунктов, для которых из предварительных вычислений находят приближённые значения t_j^o, а затем определяют поправки τ_j к этим приближённым значениям. В качестве уравниваемых величин в плановых построениях принимают измеренные направления, углы, дирекционные углы (азимуты), длины сторон сетей. Промежуточными уравниваемыми величинами (как косвенными величинами) могут явиться и приращения координат точек планового построения.

Для нахождения поправок при уравнивании параметрическим способом необходимо составить параметрические уравнения связи, которые в полной мере обеспечат решение поставленной задачи. Все измеренные величины практически можно выразить через координаты точек сети, т.е. через выбранные параметры t_j, что и требуется при уравнивании параметрическим способом. Так, дирекционные углы α и длины s сторон можно найти по разностям координат, горизонтальные углы, в свою очередь, выразить через разность дирекционных углов и т.п.

Рассмотрим различные виды уравнений поправок, применяемых при уравнивании параметрическим способом.

Уравнение поправок для измеренного дирекционного угла находится из параметрического уравнения связи между дирекционным углом и координатами точек данной линии:

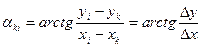(14.105)

или

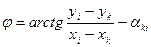. (14.106)

Известно, что и 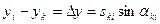. С учётом этого возьмём частные производные от функции (14.106) по переменным x и y:

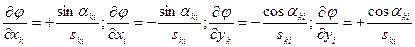. (14.107)

Свободный член l_ki уравнения поправок может быть найден из уравнения

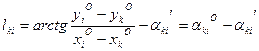, (14.108)

где х^о и у^о – значения искомых координат точек i и k, полученные по результатам предварительных вычислений по измеренным величинам; α_ki^o и α_ki' – соответственно вычисленное и измеренное значение дирекционного угла. (Вычисленные значения необходимо давать с тем же порядком точности (округления), что и непосредственно измеренные величины).

Параметрическое уравнение поправок для измеренного дирекционного угла имеет вид:

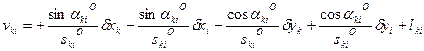. (14.109)

Выразим поправк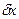и и в координаты х и у в дециметрах и обозначим их соответственно буквами ξ и η. Поправки в углы и свободный член уравнения – в секундах, а значение длины s - в километрах. С учётом этого можно записать, что

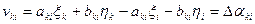, (14.110)

где

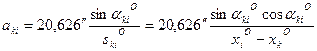, (14.111)

 

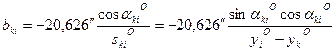(14.112)

называются коэффициентами параметрического уравнения поправок.

При этом необходимо учитывать, что величины v_ki являются поправками для измеренных углов α_ki, а величины Δ α_ki - поправками для вычисленных дирекционных углов α_ki^o.

Уравнение поправок для измеренного направления может быть получено из следующего параметрического уравнения связи:

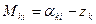, (14.113)

где М_ki – измеренное направление; z_k – ориентирующий (дирекционный) угол начального направления в точке k.

Выразим значение α_ki через выбранные параметры (14.105) и запишем параметрическое уравнение связи (14.113) в виде

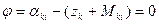(14.114)

или

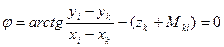. (14.115)

Если при предварительных вычислениях значение ориентирующего угла z_k^o определено с погрешностью δz_k, то для любого направления на данном пункте существует постоянная погрешность величиной δz_k.

Параметрическое уравнение поправок для измеренного направления M_ki будет иметь вид:

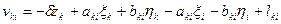, (14.116)

похожий на уравнение (14.110). Если дирекционный (ориентирующий) угол в исходном пункте получен без погрешности (т.е. погрешность его определения весьма мала по сравнению с погрешностями измерений других величин), то в выражении (14.116) можно исключить δz_k.

Свободный член уравнения поправок в направления находят по формуле

,

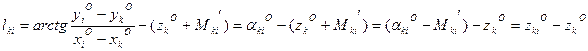(14.117)

где α_ki^о - точное значение дирекционного угла, вычисленное по координатам точек (предварительным их значениям); M_ki' - измеренное значение направления; z_ki^o - частные значения ориентирующего угла на пункте k; z_k^o - предварительное значение дирекционного (ориентирующего) угла находят как среднее арифметическое из его частных значений:

. (14.118)

В (14.118) n – число измеренных направлений на пункте k.

Отметим некоторые особенности уравнивания направлений на пункте k:

1. Сумма свободных членов на пункте должна быть равна нулю.

2. Из-за возможных погрешностей в вычислениях расстояния между пунктами следует определять дважды:

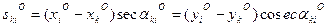. (14.119)

3. Сумма поправок в направления на каждом пункте должна быть равна нулю.

4. Уравнения поправок для прямого и обратного направлений различаются только значениями δz и свободными членами.

5. Если а) – пункт i исходный, а пункт k определяемый, либо б) – пункт i определяемый, а пункт k исходный, либо в) – оба пункта исходные, то уравнения поправок в направления имеют соответственно следующий вид:

а)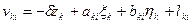

б) 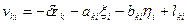(14.120)

в)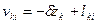

6. Порядок уравнивания направлений в триангуляции параметрическим способом следующий (в качестве измеренных величин обычно берут направления):

- вычисляют предварительные значения координат и дирекционных углов;

- составляют параметрические уравнения связи, вычисляют коэффициенты и свободные члены уравнений поправок; составляют уравнения поправок для направлений, измеренных на пункте;

- составляют и решают нормальные уравнения поправок к предварительно вычисленным координатам;

- вычисляют окончательные значения координат пунктов;

- вычисляют поправки в измеренные направления;

- выполняют контроль обработки и оценивают точность уравненных величин (элементов сети).

Уравнение поправок для угла может быть получено на основании того, что значение угла равно разности дирекционных углов двух направлений:

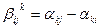(14.121)

или

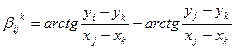. (14.122)

С учетом (14.116) можно записать, что

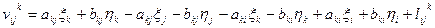(14.123)

или

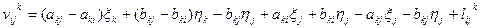. (14.124)

Вычисление свободных членов l_ij^k контролируют невязками W треугольников:

l_ij^k + l_kjⁱ + l_ik^j = - W, (14.125)

где

l_ij^k = (α_kj^o – α_ki^o) – β_ij^k и т.д. (14.126)

вычисляют из предварительных определений дирекционных углов и значениям измеренных горизонтальных углов β.

Уравнение поправок для измеренного расстояния находят из параметрического уравнения связи

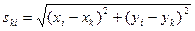(14.127)

или

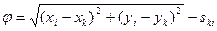. (14.128)

Если продифференцировать функцию (14.128) по переменным х и у, то получим частные производные

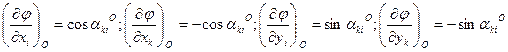. (14.129)

В этом случае параметрические уравнения поправок для измеренного расстояния будут иметь вид:

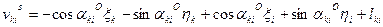, (14.130)

где

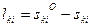, (14.131)

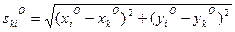. (14.132)

определяют по значениям координат х^о и у^о, полученных из предварительных вычислений, а s_ki - измеренное значение расстояния.

В уравнении поправок (14.130) все линейные величины должны быть выражены в одних и тех же единицах.

Как было сказано выше, решение задачи уравнивания параметрическим способом основано на представлении всех измеренных величин в виде функций некоторых выбранных параметров. Пусть, например, в треугольнике из n искомых элементов измерено k необходимых величин. В данном случае все избыточные элементы r можно выразить в виде их функций, т.е. здесь не возникает задачи уравнивания. Например, в треугольнике АВС измерены углы А и В и длина линии АВ = с. Остальные элементы можно найти из соотношений:

С = 180^о – (А + В);

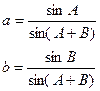(14.133)

Если же измерены избыточные (r) параметры С, а и b либо один из них, то возникает задача уравнивания.

Обозначим необходимые элементы буквой Т_j. Для указанного треугольника в этом случае имеем: А = Т₁, В = Т₂, с = Т₃. Соотношения (14.133) здесь можно записать в виде:

С = 180^о – (Т₁ + Т₂)

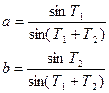(14.134)

Пусть, как и в коррелатном способе уравнивания, истинные значения Х₁, Х₂, …, Х_n (нам неизвестные) измерены, в результате чего получены значения х₁, х₂, …, х_n, из которых k – необходимые, а r =(n – k) – избыточные. Значения x_i получены с весами p_i.

Выберем такие независимые между собой параметры Т_j (j = 1, 2, …, k), функциями которых можно выразить все измеренные величины x_i (i = 1, 2,…, n) Очевидно, что число таких параметров должно быть равно k необходимых измерений. Получим функции

………………………

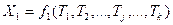
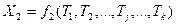
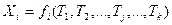(14.135)

………………………

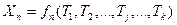
Равенства (14.135) называют параметрическими уравнениями связи.

Поскольку истинные значения Т_j бывают неизвестными, то в процессе уравнивания получают их вероятнейшие значения, а затем находят уравненные значения всех измеренных величин.

Обозначим уравненные значения параметров T_j буквой t_j, тогда

x₁' = x₁ + ν₁ = f₁ (t₁, t₂, …, t_j,…, t_k)

x₂' = x₂ + ν₂ = f₂ (t₁, t₂, …, t_j,…, t_k)

………………………………………

x_i' = x_i + ν_i = f_i (t₁, t₂, …, t_j,…, t_k) (14.136)

………………………………………

x_n' = x_n + ν_n = f_n (t₁, t₂, …, t_j,…, t_k)

Из (14.136) следует, что

ν_i = f_i (t₁, t₂, …, t_j,…, t_k) - x_i. (14.137)

Если уравнения (14.136) имеют нелинейный вид, то решение этой системы уравнений практически невозможно.

Для решения системы уравнений (14.136) для параметров t_j находят такие значения t_j^о (с такой их точностью), чтобы равенства (14.136) можно было привести к линейному виду разложением в ряд Тейлора с ограничением только членами первого порядка.

Для значений t_j можно записать, что

t_j = t_j^о + τ_j, (14.138)

где τ_j – поправки в приближенные значения параметров t_j^о. Тогда

ν_i = f_i (t₁+τ₁, t₂+τ₂, …, t_j+τ_j,…, t_k+τ_k) - x_i . (14.139)

Разложим функцию (14.139) в ряд Тейлора, ограничиваясь первыми членами разложения:

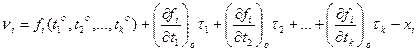. (14.140)

Введём обозначения:

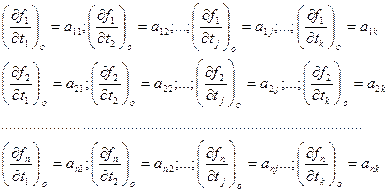(14.141)

Первый индекс при параметре а показывает номер параметрического уравнения связи (измеренной величины), а второй – номер параметра t (и поправки τ. В общем виде

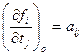. (14.142)

Найдём разности между вычисленными значениями x_i^o через приближённые значения параметров t_i^o и измеренными значениями x_i. Эти разности l_i называются свободными членами параметрических уравнений поправок:

l_i = x_i^o – x_i = f_i (t₁^o, t₂^o, …, t_j^o, …, t_k^o) - x_i. (14.143)

C учётом (14.143) систему уравнений (14.139) можно записать в развёрнутом виде:

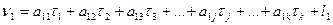
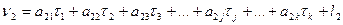
(14.144)

……………………………………………..

……………………………………………..

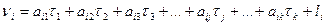
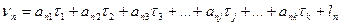
В системе n уравнений (14.144) содержится (n+k) неизвестных, в связи с чем эта система является неопределённой. Так же, как и в коррелатном способе уравнивания, решение данной системы определяется условием минимума сумм квадратов поправок, т.е. [ pv² ] = min.

Опуская промежуточные математические преобразования (о них можно посмотреть в соответствующей геодезической литературе), приведём окончательный вид системы нормальных уравнений, которая состоит из k уравнений с k неизвестными τ_j с учётом весов p_i измеренных величин и значений l_i свободных членов параметрических уравнений поправок:

[ ра₁а₁ ] τ₁ + [ ра₁а₂ ] τ₂ + [ ра₁а₃ ] τ₃ + … + [ ра₁а_k ] τ_k + [ pa₁l ] = 0

[ ра₂а₁ ] τ₁ + [ ра₂а₂ ] τ₂ + [ ра₂а₃ ] τ₃ + … + [ ра₂а_k ] τ_k + [ pa₂l ] = 0

………………………………………………………………… (14.145)

[ ра_iа₁ ] τ₁ + [ ра_iа₂ ] τ₂ + [ ра_iа₃ ] τ₃ + … + [ ра_iа_k ] τ_k + [ pa_il ] = 0

…………………………………………………………………

[ ра_nа₁ ] τ₁ + [ ра_nа₂ ] τ₂ + [ ра_nа₃ ] τ₃ + … + [ ра_nа_k ] τ_k + [ pa_nl ] = 0

В выражениях (14.145) индексы при коэффициентах а соответствуют вторым индексам коэффициентов a_ij в выражениях (14.144).

Для раскрытия гауссовых сумм в (14.145) составим матрицу коэффициентов a_ij с весами p_i результатов измерений и со свободными членами l_i (табл. 14.15).

C учётом табл. 14.15 и выражений (14.145) приведём принцип раскрытия гауссовых сумм.

Таблица 14.15

Матрица коэффициентов, свободных членов и весов

j i				…	j	…	k	li	pi
	a11	a12	a13		a1j		a1k	l1	p1
	a21	a22	a23		a2j		a2k	l2	p2
	a31	a32	a33		a3j		a3k	l3	p3
…	…	…	…	…	…	…	…	…	…
i	ai1	ai2	ai3		aij		aik	li	pi
…	…	…	…	…	…	…	…	…	…
n	an1	an2	an3		anj		ank	ln	pn

 

Уравнение 1.

Коэффициент при τ₁ равен сумме произведений веса с индексом аргумента (измеренной величины) на квадрат коэффициента 1-го столбца (диагональный коэффициент), т.е.

[ pa₁a₁ ] = c₁₁ = p₁a₁₁² + p₂a₂₁² + p₃a₃₁² +...+ p_na_n1².

Коэффициент при τ₂ равен сумме произведений веса соответствующего аргумента и коэффициентов 1-го и 2-го столбцов, т.е.

[ pa₁a₂ ] = c₁₂ = p₁a₁₁a₁₂ + p₂a₂₁a₂₂ + p₃a₃₁a₃₂ + …+ p_na_n1a_n2.

Подобные действия производятся для остальных параметров τ перемножением коэффициентов 1-го столбца и столбца с индексом τ.

Свободный член уравнения 1 равен сумме произведений веса р_i, свободного члена l_i и коэффициента a соответствующего столбца, т.е.

[ pa₁l ] = d₁ = p₁a₁₁l₁ + p₂a₂₁l₂ + p₃a₃₁l₃+ …+ p_na_n1l_n.

Уравнение 2.

Коэффициент при τ₁ равен сумме произведений веса соответствующего аргумента и коэффициентов 2-го и 1-го столбцов, т.е.

[ pa₂a₁ ] = c₂₁ = p₁a₁₂a₁₁ + p₂a₂₂a₂₁ + p₃a₃₂a₃₁ + …+ p_na_n2a_n1.

Коэффициент при τ₂ равен сумме произведений веса с индексом аргумента на квадрат коэффициента 2-го столбца (диагональный коэффициент), т.е.

[ pa₂a₂ ] = c₂₂ = p₁a₁₂² + p₂a₂₂² + p₃a₃₂² +...+ p_na_n2².

Коэффициент при τ₃ равен сумме произведений веса соответствующего аргумента и коэффициентов 2-го и 3-го столбцов, т.е.

[ pa₂a₃ ] = c₂₃ = p₁a₁₂a₁₃ + p₂a₂₂a₂₃ + p₃a₃₂a₃₃ +…+ p_na_n2a_n3.

Далее выполняются действия со 2-м столбцом и последующими оставшимися столбцами.

Свободный член уравнения 2 равен сумме произведений веса р_i, свободного члена l_i и коэффициента a соответствующего столбца, т.е.

[ pa₂l ] = d₂ = p₁a₁₂l₁ + p₂a₂₂l₂ + p₃a₃₂l₃+…+ p_na_n2l_n.

Вычисление коэффициентов остальных уравнений аналогично. Коэффициенты последнего уравнения с индексом k являются диагональными.

Здесь, как и в коррелатном способе уравнивания, коэффициенты с с противоположными индексами равны друг другу. Следовательно, достаточно определить все диагональные коэффициенты и все коэффициенты, находящиеся справа от диагональных, а остальные записать в уравнениях поправок такими же, как и противоположные им по индексам.

Таким образом, получается система линейных уравнений поправок τ_j:

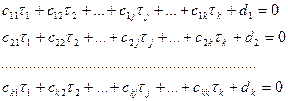(14.146)

Из решения системы уравнений (14.146) находят значения неизвестных поправок τ_j к приближенным значениям параметров t_j⁰, определяют поправки ν_i по формулам (14.144) и вычисляют уравненные значения измеренных величин и выбранных параметров T_j (t_j = t_j⁰ + τ_j).

Приведем последовательность уравнивания геодезических построений параметрическим способом.

Шаг 1. Определяют число необходимых (k), число избыточных (r) в массиве общего числа n измерений x_i, имеющих веса p_i.

Шаг 2. Осуществляют выбор параметров t_j таким образом, чтобы они не имели между собой никаких математических связей, т.е. были независимыми. Число таких параметров должно быть равно k – числу необходимых измерений. При этом все измеренные величины должны выражаться функционально через выбранные параметры t_j.

Шаг 3. Определяют вид функций значений x_i от аргументов t_j, т.е. вид параметрических уравнений связи (14.135).

Шаг 4. Вычисляют приближенные значения t_j⁰ параметров t_j. Часто для этого выполняют предварительные вычисления (обработку) в схемах геодезических построений. Иногда выполняют предварительное уравнивание упрощенными способами, часто способом раздельного уравнивания.

Шаг 5. Вычисляют по формулам (14.141), в общем виде – (14.142) или (14.144), коэффициенты a_ij и свободные члены l_i параметрических уравнений поправок v_i (14.143), т.е. функции (14.135) приводят к линейному виду.

Шаг 6. Составляют таблицу коэффициентов a_ij, свободных членов l_i и весов p_i (табл. 14.15) и с помощью неё получают нормальные уравнения (14.145), из решения которых находят значения поправок τ_j к параметрам t_j^o.

Шаг 7. Выражают поправки v_i к измеренным величинам x_i через значения поправок τ_j (14.143) и определяют их значения.

Шаг 8. Bыполняют уравнивание измеренных величин x_i' =(x_i + v_i) и параметров t_j =(t_j^o + τ_j) и контролируют правильность решения задачи по равенствам (14.135).

Возможны несоблюдения указанных равенств из-за неточного выбора параметров t_j либо их приближённых значений t_j^o. Из-за этого могли использоваться такие величины поправок, при которых необходимо было учитывать нелинейность систем уравнений. Несоблюдение равенств может быть также и из-за погрешностей в вычислениях. Поэтому в первую очередь следует выполнить повторные вычисления (контрольные, лучше во вторую руку: т.е. взаимно попросить кого-нибудь из друзей повторить Ваши вычисления, а Вы такие же вычисления повторно сделаете в его задании; поверьте, так будет и быстрее, и надёжнее).

Если уравнивание, при отсутствии погрешностей в вычислениях, не удовлетворяет условиям (14.135), то полученные значения считают их первым приближением, т.е. уточнёнными значениями t_j^o, и уравнивают систему вторично.

В качестве рекомендации следует отметить, что предварительные вычисления в уравниваемых построениях лучше выполнять после предварительного, нестрогого уравнивания. Например, в полигонометрическом ходе выполнить уравнивание углов, затем – приращений координат. В цепочке треугольников выполнить предварительное уравнивание углов отдельных треугольников и т.п.