Величина любой деформации Δ в двух сопоставляемых циклах наблюдений характеризуется разностью координат положения точки во времени между циклами 1 и 2:
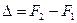, (13.11)
где F – координата точки (плановая, высотная, угловое положение, отсчёт по шкале подвижной марки, ширина трещины и др.).
Погрешность m Δ результата измерений определяется погрешностями получения координат F (mF1; mF2) по формуле
. (13.12)
При равноточных измерениях в циклах, что всегда стремятся обеспечить при практической реализации схем измерений, mF1 = mF2 = mF,
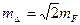. (13.13)
При неравноточных измерениях (т.е. при вынужденном изменении схемы измерений, вызванном отличающимися условиями измерений) необходимо учитывать весовые характеристики в каждом из сопоставляемых циклов.
В качестве единицы веса при наблюдениях за вертикальными перемещениями часто принимают превышение, полученное в ходе одного направления при одном горизонте прибора по двум шкалам реек при установленной в схеме измерений длине плеча D (расстояния от нивелира до реек). При определении горизонтальных смещений (в случае измерения расстояний между рабочими реперами) единицей веса может быть пролёт, измеренный в ходе двух направлений при одном уложении мерного прибора. При измерении горизонтальных углов единицей веса может явиться, например, угол, измеренный на станции одним полным приёмом при установленных сторонах D угла.
Уравнивание геодезических построений при наблюдениях за деформациями, выполненных по методикам I и II класса, производят строгими способами, при наблюдениях III и IV класса – чаще всего нестрогими способами (гл. 14).
Результаты вычисления деформаций представляют различными способами. В таблицах – когда последовательно по циклам указывают значения деформаций для каждой из точек. На графиках, которые строят в шкалах времени (номеров циклов) и величин деформаций. Для некоторых объектов целесообразно для хорошей наглядности строить прстранственно-временные графики деформаций (рис. 13.13). Указанные графики представляют собой чертёж, выполненный в принятом масштабе, на который наносят в шкале времени циклы наблюдений, а в пересечениях с ними – значения деформаций для каждой из точек. Затем интерполированием строят изолинии деформаций и выполняют анализ поведения объекта и его частей. Если на таких графиках изолинии деформаций будут параллельны горизонтальным линиям циклов, то это говорит о систематической равномерной деформации объекта. Если изолинии будут перпендикулярны линиям циклов, то это говорит о неравномерной деформации.
Другой вид графиков – пространственный (рис. 13.14). Он отражает фиксированную картину деформаций по отношению к предыдущему циклу,
Рис. 13.13. Пространственно-временной график деформаций.
Рис. 13.14. Пространственный график деформаций.
обычно – к начальному циклу, на сравнительно большой площади. Такой график также рисуется в изолиниях деформаций.
Способ интерпретации данных измерений, представленный на рис. 13.14, более применим при исследованиях значительных по площади объектов, но может быть использован и для локальных областей объектов либо для объектов в целом, если сеть наблюдаемых точек более-менее равномерно охватывает весь исследуемый объект. К недостаткам этого способа следует отнести необходимость представления динамики процесса деформирования на нескольких подобных графиках, максимально – по числу проведённых циклов измерений, за исключением первого (начального) цикла.
Способ интерпретации данных измерений, представленный на рис. 13.13, применим, вообще говоря, для объектов сравнительно простой формы и только для ограниченного числа наблюдаемых точек. Например, точек, расположенных по контуру объекта. В связи с этим способ графического отображения информации определяется исключительно возможностями полной графической передачи информации о процессе деформирования. Во многих случаях приходится обходиться только простыми графиками деформаций по каждой из наблюдаемых точек.
Глава 14
