Проблема уравнивания геодезических построений является весьма важной при выполнении измерений и их обработке в процессе создания опорных сетей на земной поверхности и в недрах (в горных выработках), при выполнении точных и высокоточных специальных работ, при наблюдениях за деформациями наземных сооружений и горных выработок и др. Основными геодезическими построениями являются плановые Государственные геодезические сети 1, 2, 3 и 4 классов, а также сети 1-го и 2-го разрядов, высотные нивелирные сети I, II, III и IV классов. Все другие построения представляют собой сравнительно локальные фигуры в месте проведения специальных инженерно-геодезических работ, например, по созданию точной геодезической разбивочной основы на строительной площадке либо аналогичных маркшейдерских работ, в том числе при прокладке полигонометрических ходов в подземных горных выработках. Такими фигурами (построениями) могут быть: небольшие цепочки треугольников триангуляции или трилатерации; вставки в угол; центральные системы; геодезические четырёхугольники; полигонометрические ходы и системы полигонометрических ходов; нивелирные ходы и системы нивелирных ходов и др.
Под уравниванием понимают комплексное решение трёх основных задач:
- определение по результатам измерений надёжных значений искомых величин, а также их функций, как косвенных результатов измерений;
- оценка точности результатов измерений;
- оценка точности функций измеренных величин.
Даже при весьма тщательных многократных измерениях одной и той же величины в каждом из результатов с большой вероятностью практически неизбежно содержится погрешность, представляющая собой, в основном, суммарное воздействие приборных погрешностей, личных погрешностей наблюдателя и погрешностей из-за влияния внешней среды. В связи с этим, даже при измерениях точно известных величин, например, суммы горизонтальных углов плоского многоугольника, возникают невязки, что приводит к неоднозначности в значениях измеренных углов. Указанная неоднозначность заключается в том, что при наличии общей невязки остается неизвестной даже абсолютно правильно измеренная величина.
Уравнительные вычисления дают возможность устранить практические невязки в различных геодезических построениях, найти вероятнейшие значения измеренных величин и выполнить оценку их точности. Хотя сама по себе неоднозначность в результатах измерений остается, поскольку существовала практическая невязка, и вероятнейшее значение измеренных величин получаются со степенью надежности всегда меньшей единицы. Здесь следует учитывать, что при введении поправок в результаты измерений какая-то из величин либо несколько из них могут быть исправлены и в худшую сторону. То есть существует вероятность того, что, например, один из углов был измерен абсолютно точно, но из-за неопределенности, возникающей при появлении невязки, он искажается на величину поправки. В то же время, измеренному с большей погрешностью углу может быть придано меньшее значение поправки.
При изложении способов уравнивания принято во внимание, что читатель изучил разделы высшей математики, в которых рассматриваются вопросы теории вероятностей и математической статистики, дифференциальное и интегральное исчисления, теория матриц и решение систем линейных уравнений, вопросы теории погрешностей результатов геодезических измерений. Этого и следует ожидать, поскольку данные вопросы будут изучаться Вами на старшем курсе.
В теории погрешностей измерений рассматриваются правила математической обработки результатов многократных измерений одной независимой величины и оценки погрешностей функций независимых величин. Эти правила могут применяться для любой совокупности измеренных величин при условии, что совокупность эта включает в себя только необходимые величины.
Необходимыми величинами, как уже отмечалось выше, являются такие независимые между собой величины, из которых можно получить для каждой искомой величины только одно единственное её значение. В геодезической и маркшейдерской практике обычно измеряют, как уже говорилось раньше, кроме необходимых и избыточные величины. Например, три стороны треугольника и один, два или все три его угла, не (n – 1) угол многоугольника, а все его углы.
Обозначим число необходимых измерений буквой k, число избыточных измерений буквой r, тогда полное (общее) число измерений n = k + r.
Предположим, что нами измерены все внутренние углы в полигоне, состоящем из n вершин. В этом случае число необходимых измерений составит k = n – 1, а число избыточных измерений r = 1. Каждый из измеренных углов, а также любые (n –1) углов, не позволяют составить математическое соотношение для суммы углов многоугольника, можно только вычислить значение неизмеренного угла. Однако для полной группы n измеренных углов
 , (14.1)
, (14.1)
где  - сумма точных значений горизонтальных углов; i = 1, 2, 3, …, n; знак «плюс» за круглыми скобками - для внешних углов, знак «минус» - для внутренних углов.
- сумма точных значений горизонтальных углов; i = 1, 2, 3, …, n; знак «плюс» за круглыми скобками - для внешних углов, знак «минус» - для внутренних углов.
Введём в сумму точных значений углов значения βi измеренных углов. В этом случае можно записать, что
 , (14.2)
, (14.2)
где W – невязка, определяющая степень нарушения условия (14.1) и возникающая из-за неизбежных погрешностей в результатах измерений.
Процесс уравнивания здесь заключается в ликвидации невязки, т.е. определении таких значений углов βi´, при которых обеспечивается выполнение условия (14.1), т.е.
 . (14.3)
. (14.3)
Вероятность – вещь в природе закономерная, поэтому в формуле (14.2) может получиться, что невязка будет равна нулю. С одной стороны – это хорошо, это значит, что правильно выполнены измерения. С другой стороны – это не значит, что все измеренные углы получились с нулевой погрешностью, т.е. абсолютно точными. Просто великий закон случайности и вероятности позволил скомпенсировать (случайно, конечно) погрешности в группе измеренных углов. Вот об этом не надо никогда забывать.
Можно сформулировать следующие основные выводы:
- уравнивание возможно только при наличии избыточных измерений, а также при условии неизбежного появления малых по величине (допустимых) погрешностей измерений необходимых и избыточных величин;
- уравнивание состоит в определении невязок в составленных математических соотношениях путем введения поправок vi в результаты измерений и в нахождении вероятнейших значений искомых величин; для рассмотренного выше примера
 ; (14.4)
; (14.4)
- избыточные измерения являются необходимым процессом для контроля и оценки точности результатов измерений.
И вот, вернёмся к тому, как сказано, что «уравнивание возможно … при условии неизбежного появления малых по величине (допустимых) погрешностей». Так что появление невязки, равной нулю, создаёт некоторую неопределённость для уравнивания. Но при обработке сравнительно сложных линейно-угловых построений в каких-то их частях появится невызка. Как сказано – неизбежно.
Если при измерении n величин (k необходимых и r избыточных, причём r < n) получены результаты х1, х2, …, хn, точность которых определяется их весами р1, р2 , …, рn, то можно составить r условных уравнений (14.1):
φ1 (хo1, xo2, …,xoi,…, xon) = 0
φ2 (хo1, xo2, …,xoi,…, xon) = 0
…………………………….
φj (хo1, xo2, …,xoi,…, xon) = 0 (14.5)
……………………………
φr (хo1, xo2, …,xoi,…, xon) = 0
где i = 1, 2, 3, …, n; j = 1, 2, 3, …, r.
Очевидно, что система условных уравнений (14.5) является неопределенной, поскольку содержит r уравнений с n неизвестными при r < n.
Значения хi содержат погрешности. Если ввести в уравнения (14.5) вместо значений хoi измеренные значения хi, то получим другую систему уравнений, подобную (14.2):


………………………… (14.6)

…………………………

Устранение невязок Wi заключается во введении в значения х i поправок vi и получения уравненных значений результатов измерений:
хi´ = хi + vi, (14.7)
т.е.


……………………………………………….. (14.8)

………………………………………………..

или, с учетом (14.7),


…………………………
 (14.9)
(14.9)
…………………………
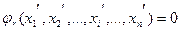
Непосредственно технология уравнивания заключается в нахождении единственных значений поправок vi при множестве решений неопределенной системы уравнений (14.8) или (14.9). Для решения таких задач используется метод наименьших квадратов.






