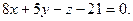Предметом аналитической геометрии является изучение гео- метрических фигур и их свойств при помощи действий с чис -лами и наборами чисел, однозначно определяющих геометри -ческие фигуры.
§ 1. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
УРАВНЕНИЕ С ДВУМЯ НЕИЗВЕСТНЫМИ. Рассмотрим равенство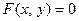 
, где 
- переменные величины, принимающие различные действительные значения, 
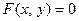- некоторое выражение (композиция известных функций) со- держащее . Если равенство выполняется для всех значений , то оно называется тождеством. Если же равенство 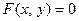выплоняется не для всех пара чисел , то оно называется уравнением линии на плоскости. Простейшим уравнением линии на плоскости яв- ляется уравнение прямой.
Из школьного курса известно уравнение прямой с угловым коэффициентом: 
, где 
, 
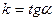. (1)
Если мы знаем угол наклона прямо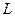й к оси 
, т.е. если задан угловой коэффициент этой прямой 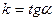и задана фиксированная точка на прямой 
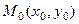, то, чтобы напи- сать уравнение прямой, удобно воспользоваться формулой:
(2)
Уравнение (1) получится из уравнения (2), если раскрыть скобки и привести подобные.
Например: Написать уравнение прямой, проходящей через точку 
под углом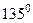 
к оси .
Угловой коэффициент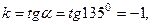 
тогда, по фор- муле (2), прямая имеет уравнение:: 
, или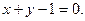 
Рассмотрим произвольную прямую 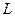на плоскости. Пусть 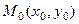- фиксированная, а 
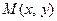текущая точки дан -ной прямой.
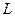
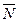
Если заданы векторы 
, перпендикулярный прямой (нормаль или нормальный вектор), или 
, парал -лельный данной прямой (направляющий вектор), то, исполь- зуя условия ортогональности и коллинеарности, можем напи -сать уравнения прямой 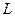следующим образом:
; следовательно, 
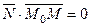, или
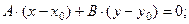(3)
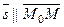; следовательно координаты этих векторов пропор- циональны и получаем:
. (4)
В частности, если на прямой заданы две точки 
и 
, то вектор 
являет- ся направляющим вектором прямой 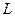и её уравнение принимает вид:
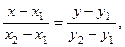(5)
Уравнение прямой по двум заданным точкам.
Пример 1 Написать уравнение прямой, проходящей через точку 
а) перпендикулярно вектору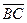 
; б) парал – лельно вектору 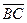, если 
; с) написать уравнение прямой, проходящей через точки 
и .
. Тогда в случае а) 
и, по формуле (3), уравнение имеет вид: 
или 
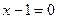; в случае б) получим уравнение: 
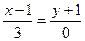, по формуле (4), или 
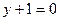; в случае с), по формуле (5), получаем уравнение: 
, или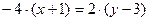 
, 
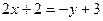. Таким образом получаем: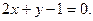 
Если в равенстве (3) откроем скобки, то получим общее уравнение прямой на плоскости:
(6)
является нормальным вектором данной прямой.
Если известны длины отрезков, которые прямая отсекает на осях координат,
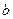
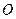
то уравнение этой прямой можно записать следующим об -разом:
(7)
§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ НА
ПЛОСКОСТИ
Пусть заданы уравнения двух прямых на плоскости:
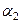
Тогда
.
Следовательно, угол между прямыми 
(учитывая смысл угловых коэффициентов прямых) определяется по формуле:
(1)
Если прямые параллельны, т.е. 
, то 
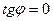и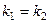 
; если прямые перпендикулярны, 
, то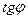 
не существу- ет, то 
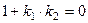, или 
(это условие перпендику-
лярности прямых).
Пример 1. Даны две противоположные вершины квадрата:
. Найти уравнения сторон квадрата.
Зная координаты точек и можем найти координаты точки 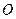, как координаты середины отрезка, (т.е. полусумма координат концов отрезка): 
. Кроме того можем напи- сать уравнение прямой 
, как уравнение прямой проходя- щей через две заданные точки (формула (5) § 1):
Тогда 
Угол между прямыми 
и равен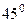 
. Следовательно, по формуле (1),
.
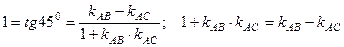Отсюда, 
Зная координаты точки 
и угловой коэффициент 
(по формуле (2) § 1
), можем написать уравнение прямой:
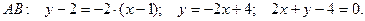
Прямые и 
параллельны; тогда 
. Прямая (при использовании координат точки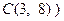 
имеет уравнение:
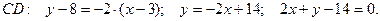
; учитывая условие перпендикулярности прямых,
. Используя то же уравнение, получим:
И наконец 
и тогда:
Пример 2. Пусть даны координаты одной вершины треу -гольника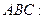 
и уравнения высоты 
и медианы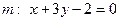 
, проведённых из разных вершин. Найти уравнения сторон треугольника.
, 
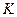
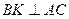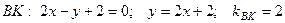. Тогда 
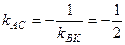и сторона имеет уравнение:
Пусть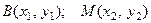 
. Точка - середина отрезка . Тогда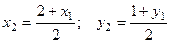 
. Точка 
и её координаты удовлетворяют уравнению: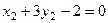 
, т.е. 
Точка 
и её координаты удовлетворяют уравнению данной прямой: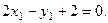 
Получаем систему:
Решение этой системы: 
, т.е. 
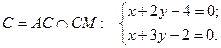
Решая систему, получаем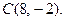 
Уравнения прямых и 
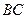можем написать, использовав уравнение прямой, проходя- щей через две заданные точки:
В случае, если прямые на плоскости заданы общими уравнениями, т.е.
то угол между ними равен углу между их нормальными векто- рами 
, т.е.
Если 
Это условие парал- лельности прямых.
Если 
Это ус -ловие перпендикулярности прямых.
§ 3. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ.
Можно усмотреть аналогию между понятиями прямой на плоскости и плоскостью в пространстве. Основой этой анало- гии является известный факт, что через заданную точку плос- кости можно провести единственную прямую, перпендикулярно заданному вектору, а через заданную точку пространства мож- но провести единственную плоскость, перпендикулярную задан- ному вектору. Следует заметить также, что размерность пря – мой равна 1, размерность плоскости - 2, размерность прост -ранства - 3, т.е. прямая в плоскости и плоскость в пространс- тве имеют одинаковую коразмерность. Линейное пространство размерности на единицу меньшей, чем размерность пространс- тва, частью которого оно является, называется гиперплоскос -тью. В соответствии с этим определением, прямая - это ги -перплоскость на плоскости, а плоскость - это гиперплоскость в пространстве.
Пусть плоскость 
проходит через точку фиксированную точку пространства 
перпендикулярно вектору 
Пусть 
- произвольная (текущая) точка данной плоскости.
Тогда уравнение плоскости получаем, используя условие ортогональности (перпендикулярности) вектора 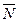и вектора 
, т.е. 
Таким образом,
(1)
Если в данном равенстве раскроем скобки, то получим общееуравнение плоскости:
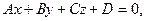(2)
где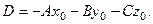 
Пример 1. Написать уравнение плоскости, проходящей через точку 
перпендикулярно вектору 
, где 
.
В данном случае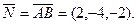 
Фиксированная точка - это точка и уравнение плоскости принимает вид:
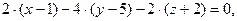
или 
Таким образом, чтобы написать уравнение плоскости необ – ходимо знать какую– нибудь точку на плоскости и вектор, пер- пендикулярный плоскости.
Часто встречается следующая задача: написать уравнение плоскости, проходящей через три заданные точки.
Пусть заданы три фиксированные точки плоскости: 
, а - текущая точка плоскости. Тогда векторы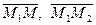 
и 
компланарны.
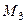
Следовательно, смешанное произведение этих векторов равно нулю:
, или
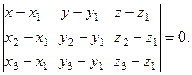(3)
Расстояние от точки до плоскости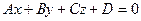 
можно найти по формуле (аналогичной формуле расстояния от точки до прямой на плоскости):
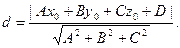(4)
Пример 2. Дана треугольная пирамида с вершинами
.
Написать уравнение плоскости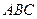 
и найти высоту, опущен- ную на эту плоскость из точки 
По формуле (3) уравнение плоскости 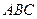имеет вид:
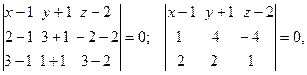
тогда 
Получаем: 
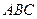т.е. плоскость имеет уравнение: 
Высоту пира -миды, опущенную из точки можно найти как расстояние от этой точки до плоскости , по формуле (4).
Используя условие компланарности векторов, можно анало -гичным образом написать уравнение плоскости, проходящей че- рез фиксированную точку пространства парал -лельно двум заданным векторам:
, 
.
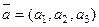В этом случае: векторы 
компланарны и их смешанное произведение равно нулю: 
т.е.
(5)
Пример 3. Написать уравнение плоскости , проходящей через точку 
перпендикулярно плоскостям:
. 
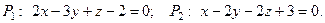
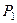
, тогда, по формуле (5), уравнение плос -кости имеет вид: 
Получаем: 
, или, окончательно, получаем уравнение плоскости 
