Примеры. Найти ранги следующих матриц:
1.  ˜
˜
Получим нули в первом столбце. Для этого умножим первую строку на (-1) и прибавим к второй строке; умножим ту же строку на (-5) и прибавим к третьей строке и, аналогично, ум- ножим её на (-7) и прибавим к четвёртой строке. Получим:
˜  ˜
˜
Умножим вторую строку на (-2) и прибавим соответственно к третьей и четвёртой
˜  ˜
˜  .
.
Следовательно ранг этой матрицы 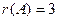 .
.
2. 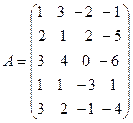 ˜
˜
С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-2) и прибавим к второй строке, умножим на (-3) и прибавим к третьей и пятой строке, умно- жим на (-1) и прибавим к четвёртой строке. В результате получим:
˜  ˜
˜
Вторую строку умножим на (-1) и прибавим к третьей, чет -вёртую строку умножим на (-4) и прибавим к пятой:
˜  ˜
˜
Пятую строку умножим на (5) и прибавим к второй и умножим на (2) и прибавим к четвёртой:
˜  ˜
˜
четвёртую строку умножим на (-3) и прибавим к второй:
˜  ˜
˜  .
.
Ранг этой матрицы тоже равен 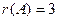 .
.
При исследовании систем важную ролю играет следующая теорема:
ТЕОРЕМА (Кронекера – Капелли). Ранг основной матрицы системы не превосходит ранга расширенной матрицы, т.е.
 , причём, если
, причём, если 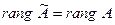 , то система совместна, а если
, то система совместна, а если  , то система несовместна (не имеет решений.
, то система несовместна (не имеет решений.
Рассмотрим пример.
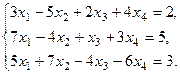
 Тогда
Тогда
 ˜
˜
Умножим первую строку на (-2) и прибавим к второй и треть- ей строке; после этого поменяем местами первую и вторую строки:
 |  | ||
˜  ˜
˜  ˜
˜
прибавим к второй, а после этого прибавим к третьей:
 ˜
˜  ˜
˜
После этого прибавим вторую строку к третьей и получим матрицу:
 ˜
˜  .
.
В результате получили матрицу, у которой
 , следовательно, система несовместна. Решений нет.
, следовательно, система несовместна. Решений нет.
Если 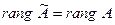 , т.е, если система совместна, то в случае, если
, т.е, если система совместна, то в случае, если  - число неизвестных, система имеет единственное решение. Если же
- число неизвестных, система имеет единственное решение. Если же  , то система имеет бесконечно много решений, при этом число свободных переменных (т.е. переменных, через которые можно выразить все остальные и которые могут принимать любые значения из множества действительных чисел)
, то система имеет бесконечно много решений, при этом число свободных переменных (т.е. переменных, через которые можно выразить все остальные и которые могут принимать любые значения из множества действительных чисел)  , а число ба -зисных переменных (т.е. таких переменных, которые выражаем через свободные) равно
, а число ба -зисных переменных (т.е. таких переменных, которые выражаем через свободные) равно 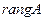 .
.
Рассмотрим примеры: решить системы уравнений методом Гаусса; найти общие и частные решения; сделать проверку.
1. 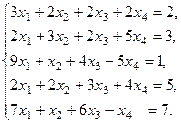
Запишем расширенную матрицу данной системы:


 ˜
˜
Уменьшим элементы первого столбца с помощью четвёртой строки. Для этого умножим её на (-1) и прибавим к первой и второй строке; умножим на (-4) и прибавим к третьей строке и, наконец, умножим на (-3) и прибавим к пятой строке.

 ˜
˜  ˜
˜
Теперь получим нули в первом столбце. Умножим первую строку на (-1) и прибавим к третьей и пятой строке; умножим её же на (-2) и прибавим к четвёртой строке. Получим:

 ˜
˜  ˜
˜
С помощью второй строки получим нули во втором столбце. Для этого умножим её на (7) и прибавим к третьей строке; умножим на (-2) и прибавим к четвёртой строке; умножим на (5) и прибавим к пятой строке:

 ˜
˜ 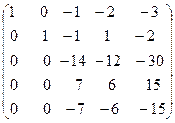 ˜
˜
Четвёртую строку умножим на (2) и прибавим к третьей строке и её же просто прибавим к пятой строке:
 ˜
˜ 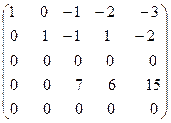 .
.
Видим, что в данном случае 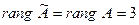 , поэтому система совместна, но так как переменных 4, а ранг матрицы равен 3, то одна переменная свободная, а три базисных. За – пишем полученную систему:
, поэтому система совместна, но так как переменных 4, а ранг матрицы равен 3, то одна переменная свободная, а три базисных. За – пишем полученную систему:

Выберем свободную переменную 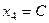 , тогда из третьего уравнения
, тогда из третьего уравнения  ; из второго уравнения
; из второго уравнения

из первого уравнения
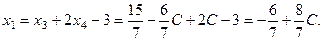
Таким образом, общее решение системы имеет вид:
 ,
,
т.е. при любом значении  мы будем получать решения сис -темы. Это общее решение Задавая какие – либо значения по -стоянной
мы будем получать решения сис -темы. Это общее решение Задавая какие – либо значения по -стоянной  , будем получать частные решения. Например, при
, будем получать частные решения. Например, при  получаем частное решение
получаем частное решение

Сделаем проверку:

Получили тождественные равенства. Аналогично можно полу- чать другие частные решения и делать проверку. Например, при  :
:  . Подставив эти значения в уравнения системы, снова получим тождес -твенные равенства. Таким же образом, при разных значениях
. Подставив эти значения в уравнения системы, снова получим тождес -твенные равенства. Таким же образом, при разных значениях  можем получить любое частное решение системы.
можем получить любое частное решение системы.
Ещё одна система:
2. 
Её расширенная матрица имеет вид:

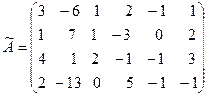 ˜
˜
Поменяем местами первую и вторую строки:

 ˜
˜  ˜
˜
С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-3) и прибавим к второй строке; умножим на (-4) и прибавим к третьей строке; умножим на
(-2) и прибавим к четвёртой строке, получим:

 ˜
˜  ˜
˜
 Вторую строку умножим на (-1) и прибавим к третьей и чет –вёртой, получим
Вторую строку умножим на (-1) и прибавим к третьей и чет –вёртой, получим
˜  .
.
Видим, что ранг полученной матрицы равен
 .
.
Поэтому система совместна. Число базисных переменных рав- но рангу матрицы, т.е. две базисные переменные Число сво -бодных переменных равно разнице «число переменных» = 5 минус «ранг матрицы» = 2, т.е 3 свободные переменные.
Запишем полученную систему:
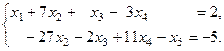
В качестве базисных переменных, если есть возможность, удобно выбрать переменные с единичными коэффициентами, чтобы избежать вычислений с дробными выражениями. Напри- мер, в данном примере, в качестве базисных можем выбрать 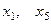 , а остальные считать свободными, т.е. положим:
, а остальные считать свободными, т.е. положим:

Тогда из второго уравнения:
 ,
,
а из первого уравнения:
 .
.
Следовательно, общее решение имеет вид:
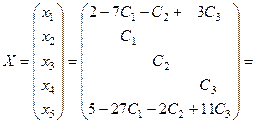

Запишем частное решение и сделаем проверку. Например, при  получим:
получим:

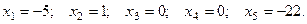
Сделаем проверку:


Получили тождественное равенство. Аналогичным образом можно получить любое другое частное решение, например, при  получим:
получим:
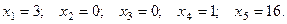
Подставив эти значения переменных в уравнения системы, также получим верные равенства.
ОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Отдельно следует выделить множество однородных уравнений, т.е. уравнений вида:

Такие системы всегда совместны, так как всегда имеется тривиальное (т.е. нулевое решение  ).
).
Нулевое решение будет единственным, если ранг основной матрицы системы равен числу неизвестных, т.е. в случае  . Если же
. Если же  , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Рассмотрим примеры: найти фундаментальные системы ре -шений однородных систем линейных уравнений
1. 
Для однородных систем нет смысла писать расширенную мат- рицу, так как элементарные преобразования не меняют нули, стоящие в правых частях системы уравнений. Поэтому про -изводим преобразования основной матрицы системы:
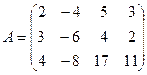 ˜
˜
Вторую строку умножим на (-1) и прибавим к первой и тре -тьей строке, получим:
˜ 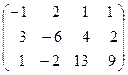 ˜
˜
С помощью первой строки получим нули в первом столбце, для чего умножим её на (3) и прибавим к второй строке и просто прибавим к третьей строке:
˜  ˜
˜
Умножим вторую строку на (-2) и прибавим к третьей:
˜  .
.
Итак, 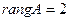 , т.е в решении данной системы 2 базисные переменные и две свободные. Запишем полученную систему:
, т.е в решении данной системы 2 базисные переменные и две свободные. Запишем полученную систему:


Из второго уравнения: 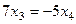 , чтобы упростить вычисле –ния, удобно положить
, чтобы упростить вычисле –ния, удобно положить  , тогда
, тогда  . Тогда пер -вое уравнение принимает вид:
. Тогда пер -вое уравнение принимает вид:  . Необходимо ввести ещё одну свободную переменную, напри – мер
. Необходимо ввести ещё одну свободную переменную, напри – мер  . Тогда
. Тогда  . В этом случае, общее решение имеет вид:
. В этом случае, общее решение имеет вид:
 .
.
Каждый из векторов:
 и
и 
является решением системы. В самом деле, для вектора  :
:
 для вектора
для вектора  :
:
 и любая комбинация этих решений также является решением системы, т.е. общее решение исходной однородной системы имеет вид:
и любая комбинация этих решений также является решением системы, т.е. общее решение исходной однородной системы имеет вид:  , а сами векторы
, а сами векторы 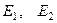 об- разуют фундаментальную систему решений данной однород- ной системы линейных уравнений.
об- разуют фундаментальную систему решений данной однород- ной системы линейных уравнений.
2. 
Запишем её матрицу:
 ˜
˜
Умножим первую строку на (-1) и прибавим к третьей и четвёртой строке:
˜  ˜
˜
Вторую строку прибавим к третьей:
˜  ˜
˜
Поменяем местами третью и четвёртую строки:
˜  .
.
Все элементы ниже главной диагонали равны нулю. Поэтому  . Неизвестных 6. Поэтому решение системы имеет 4 базисных переменных и 2 свободные. Запишем полученную систему:
. Неизвестных 6. Поэтому решение системы имеет 4 базисных переменных и 2 свободные. Запишем полученную систему:

Выберем в качестве свободных переменных  Тогда из четвёртого уравнения
Тогда из четвёртого уравнения  так как из тре -тьего уравнения
так как из тре -тьего уравнения 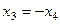 , то
, то  Из второго уравнения
Из второго уравнения
 Из первого уравнения:
Из первого уравнения:

Тогда общее решение имеет вид:

Векторы 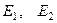 образуют фундаментальную систему реше-ний. Проверьте самостоятельно, что каждый из этих векторов является решением системы.
образуют фундаментальную систему реше-ний. Проверьте самостоятельно, что каждый из этих векторов является решением системы. 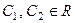 , т.е. произвольные постоянные.
, т.е. произвольные постоянные.






