Глава 2. Элементы векторной алгебры

§ 1. ВЕКТОР. АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ С

ВЕКТОРАМИ.

 

Различают понятия величин, которые характеризуются од -ним числом - скалярные величины (например: масса, объём, длина, площадь и т.д.) и величин, для которых имеет значе -ние не только их численное значение, но и направление их действия - векторных величин (например: сила, скорость, ус - корение и т.д.).

Вектором называется направленный отрезок , где - начало вектора, - конец вектора.

В физике важное значение имеет точка приложения вектора, т.е. начальная точка . Векторы в математике чаще всего не связывают с точкой приложения, поэтому часто геометрический вектор обозначается . Чтобы объяснить это, введём сначала несколько понятий. Длина вектора обозначается или . Вектор, начало и конец которого совпадают, называется нулевым. Его длина равна нулю. Считается, что его направление совпадает с направлением любого вектора, и он обозначается .

Векторы, лежащие на одной прямой, или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости, или в параллельных плоскостях, называются компланарными.

Векторы называются равными, если они коллинеарны, име- ют одинаковую длину и одинаково направлены.

Из этого определения следует, что векторы равны, если их можно совместить с помощью параллельного переноса. Равен-ство векторов не зависит от их начальных точек (точек прило- жения); таким образом, начальную точку любого вектора с помощью параллельного переноса можно совместить с любой точкой плоскости или пространства. В этом смысле геометри- ческие векторы называются свободными.

 

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

1. Сложение векторов. Суммой двух векторов и называется вектор , идущий из начала вектора в конец вектора .

 

 

 

Это определение называется правилом треугольника сложе - ния векторов. Другое определение суммы векторов называется правилом параллелограмма: вектор суммы векторов направлен по диагонали параллелограмма, построенного на векторах и , т.е

 

 

2. Умножение вектора на число. При умножении вектора на число получаем вектор , коллинеарный данному вектору, длина которого изменяется в раз, причём на- правление вектора сохраняется, если и меняется на противоположное, если .

Из сказанного выше следует ещё одно определение кол – линеарности векторов.

ОПРЕДЕЛЕНИЕ 1. Вектора 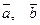называются коллинеар- ными, если существует некоторое действительное число , такое, что .

Операции сложения и умножения вектора на число обладают следующими свойствами:

1. (коммутативность сложения);

2. (ассоциативность сложения);

3.

4.

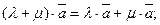
5.

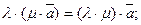
6. .

7. .

Вычитание векторов на картинке выглядит следующим обра- зом:

Вектор разности направлен в сторону вектора, из которого вычитается второй вектор.

 

Дальнейшее изучение векторов связано с понятием систе- мы координат

 

§ 2 СИСТЕМЫ КООРДИНАТ НА ПРЯМОЙ, НА ПЛОСКОС-

ТИ И В ПРОСТРАНСТВЕ.

 

1. Координата на прямой вводится следующим образом: на прямой стрелкой указывается направление положительного изменения, определяется начало отсчёта - точка О и опре –деляется масштабная единица

 

1

Координатой произвольной точки называют длину отрезка , вычисленную в масштабных единицах (в данном случае, координата точки равна ), причём, если точка находится правее точки , то знак координаты по- ложительный, а если левее, то отрицательный. Если даны две точки на прямой 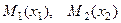, то расстояние между ни -ми ищется по формуле:

. (1)

2. Декартова (прямоугольная) система координат на пло-скости задаётся двумя взаимно перпендикулярными осями. Точка их пересечения - это начало координат, на каждой оси вводится масштабная единица.

 

1

 

О 1

 

Ось называется осью абсцисс, ось - осью ординат.

Координатами произвольной точки в данной системе ко- ординат называются числа , вычис -ленные в масштабных единицах, причём эти координаты будут положительными, если точка расположена правее (выше) соответствующей координатной оси. В данной системе коор –динат: .

Расстояние между двумя точками и на плоскости вычисляется по формуле:

. (2)

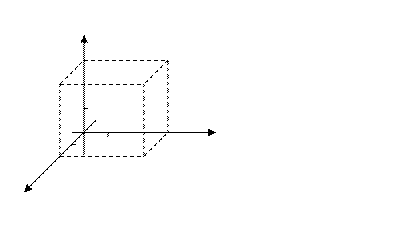3. В пространстве декартова (прямоугольная) система ко -ординат определяется осями, которые лежат в пересечениях трёх взаимно перпендикулярных плоскостей, пересекающихся в одной точке. Сами эти плоскости называются координатными плоскостями 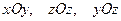, соответственно. На каждой оси вводится масштабная единица

 

 

1

Ось называется осью аппликат. Точка в пространстве имеет три координаты . Расстояние между двумя точками и в пространстве опре- деляется по формуле, которая аналогична соответствующей формуле для плоскости:

(3)

 

4. Чтобы установить связь между векторами и системой ко-

ординат, требуется ввести понятие проекции вектора на ось.

Пусть дана произвольная ось и некоторый вектор :

 

 

 

 

 

Величина направленного отрезка с соответствующим знаком оси называется проекцией вектора на ось и обозначается . Из рисунка видно, что:

.

Если угол острый, то проекция положительна, если тупой, то проекция отрицательна. Проекции равных векторов на одну и ту же ось равны.

Проекции векторов имеют два основных свойства:

1. Проекция суммы векторов равна сумме их проекций.

 

 

 

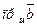
Из рисунка видим, что

.

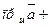
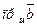2. При умножении вектора на число его проекция умно -

жается на то же число:

.

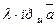Рассмотрим произвольный вектор и его проекции на оси координат. Вектор однозначно определяется своими проекция -ми на оси координат. (Равные векторы можно совместить параллельным переносом и они имеют одинаковые проекции, и наоборот, векторы с одинаковыми проекциями равны.)

Считаем, что вектор имеет проекции на оси координат равные, соответственно, . Причём, если вектор , где 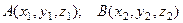, то координа- ты вектора равны, соответственно,

Таким образом, чтобы найти координаты вектора (т.е. его проекции на оси координат) необходимо из координат - конечной точки вектора вычесть соответствующие коорди- наты точки - начальной точки вектора.

 

 

 

 

 

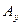
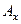
Вектор называется радиус – вектором точки . Из треугольника :

.

Тогда из треугольника имеем:

В частности, для вектора получаем: 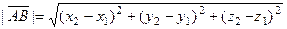, т.е. длина вектора равна расстоянию между точками A и В.

Если - угол между вектором и осью , 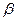- угол между вектором и осью и - угол между вектором и осью , то , , , то получаем понятия, так называемых направляющих косинусов вектора:

; ;

.

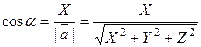Основное свойство направляющих косинусов, которое легко проверяется непосредственно:

(!)

Рассмотрим пример: найти вектор , длина которого , который образует равные острые углы с осями координат.

По условию: 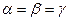, поэтому, по свойству (!),

. (знак «+», так как углы острые), тогда .

Таким образом, вектор имеет координаты:

 

Рассмотрим задачу о делении отрезка в данном отноше -нии. Пусть даны две точки . Требуется найти координаты точки , которая делит отрезок в отношении , т.е отношение длин отрезков

 

Рассмотрим случай проекций на ось . (Для остальных осей формулы получаются аналогичным образом).

 

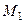
Так как параллельные прямые отсекают на сторонах угла пропорциональные отрезки, то

Тогда Таким образом,

, аналогично, ; .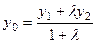

В частности, если 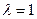, т.е. отрезок делится пополам, получаем координаты середины отрезка:

; ; . (+) Таким образом, координаты середины отрезка равны полу -сумме координат концов отрезка.

Пример. Найти координаты центра масс треугольника с 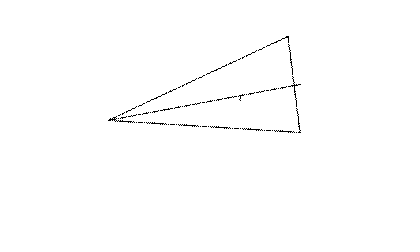вершинами:

 

 

 

О

 

 

 

Центр масс треугольника всегда находится в точке пересече -ния медиан, а медиана треугольника делит сторону пополам, тогда, по формулам (+), точка имеет координаты

, или .

Другое свойство медиан треугольника: медианы в точке пере- сечения делятся в отношении 2: 1, считая от вершины треу –гольника, поэтому точка - центр масс (точка пере -сечения медиан) делит отрезок в отношении:

.

Тогда

Таким образом .

Вернёмся снова к линейным операциям над векторами.

Пусть даны два вектора . Тогда, учитывая свойства проекции вектора на ось, получаем следующие правила:

1)

2)

3)

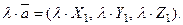
Из последней формулы, учитывая определение коллинеарнос- ти векторов, получаем следующее условие коллинеарности:

.

Рассмотрим пример: пусть даны два вектора

.

Проверить коллинеарность векторов .

Найдём координаты векторов:

Проверим выполнение условия коллинеарности:

Координаты векторов пропорциональны, следовательно векторы коллинеарны, т.е. .

В заключение, придадим другой смысл проекциям вектора на координатные оси. С этой целью в заданной системе координат определим тройку векторов следующим образом:

1) векторы лежат на осях , соответст- вено, т.е. взаимно перпендикулярны. Их направления совпада- ют с положительными направлениями соответствующих коор -динатных осей;

2)

Единичные взаимно перпендикулярные векторы по другому называются ортами. В системе координат эти векторы имеют следующие координаты:

Тогда любой вектор 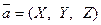можно записать следу- ющим образом: , т.е. любой вектор прост –ранства можно представить в виде линейной комбинации век- торов . Таким образом, векторы представляет собой естественный базис прямоугольной системы координат в пространстве.

ЗАМЕЧАНИЕ. Любые три некомпланарных вектора прост –ранства образуют его базис, т.е. любой другой вектор прост- ранства можно представить в виде линейной комбинации этих векторов.

 

§ 3. НЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.

 

Нелинейными операциями являются операции умножения векторов.

 

1. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т.е.

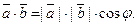(1)

Так как , , то получаем:

= (2)

Отсюда получаем формулы для вычисления проекций:

; . (3)

Также, учитывая формулу (1),

. (4)

Скалярное произведение векторов имеет простой механи – ческий смысл: Скалярное произведение равно работе силы по перемещению материальной точки из начала в конец вектора .

 

Легко доказать следующие свойства скалярного произ –ведения:

1. = (коммутативность);

2. =

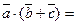
3. (дистрибутивность);

4. тогда ;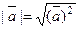

5. Условие ортогональности векторов:

,

так как .

 

Эти свойства позволяют выполнить следующие задания:

1). Пусть ; угол между этими векторами . Найти длину вектора .

 

По свойству 4,

2). Пусть ; угол между этими векторами 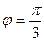. Найти .

По формуле (3), 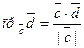. В данных условиях,

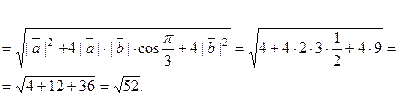
Тогда .

 

Пусть теперь векторы заданы своими координатами:

в базисе . При вы- числении скалярного произведения базисных векторов получим: , по свойству 4. Аналогично 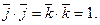Так как векторы ортогональны, т.е. попарно перпендику –лярны, то, по свойству 5, Тогда

Таким образом, скалярное произведение векторов, заданных координатами, равно сумме произведений соответствующих координат:

(5)

Тогда векторы ортогональны если

Угол между векторами и можно найти по формуле:

 

= . (6)

Рассмотрим ещё несколько примеров:

1. Даны векторы . При

каком значении эти векторы перпендикулярны?

. , так как векторы перпендикулярны. Тогда или

2. Треугольник задан своими вершинами: А(2, -1, 3),

В(1, 1, 1), С(0, 0, 5). Найти углы треугольника АВС.

, тогда по формуле (6),

Следовательно .

тогда по той же формуле,

и угол 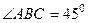. Тогда .

3. Проверить, что четырёхугольник с вершинами: является квадратом.

 

 

 

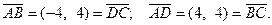
Следовательно, противоположные стороны параллельны и оп- ределяются одинаковыми векторами. Тогда данный четы- рёхугольник является параллелограммом. Найдём длины смеж- ных сторон: . Т.е. все стороны равны. Параллелограмм с равными сторонами является ромбом. Чтобы доказать, что ромб является квадратом, достаточно доказать перпендикулярность хотя бы двух смежных сторон. Найдём скалярное произведение:

Выполнено условие ортогональности векторов и 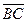, сле- довательно , и тогда рассматриваемый четы- рёхугольник является квадратом.

 

2. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

 

Векторным произведением вектора на вектор называ- ется вектор, обозначаемый , или , который опреде- ляется тремя условиями:

1) Вектор перпендикулярен векторам и , т.е. :

2) Длина вектора - :

3) Векторы образуют «правую тройку».

 

Векторы образуют правую

тройку, если они имеют общее на-

чало и из конца вектора крат -

чайший поворот вектора к век –

тору виден против часовой

стрелки.

 

Механический смысл векторного произведения: вектор- ное произведение равно моменту силы , при -ложенной к концу вектора относительно начала век -тора .

 

Свойства векторного произведения.

1. ;

Если поменяем местами векторы , то тройка

векторов поменяет ориентацию (станет левой)

и вектор сменит направление на противополож-

ное.

2. Если векторы имеют одно и то же начало, то

модуль (длина) векторного произведения численно ра –

вен площади параллелограмма, построенного на век –

торах (произведение длин сторон на синус угла

между ними). Таким образом:

площадь параллелограмм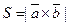а , а

площадь треугольника

3. Если векторы коллинеарны, то их векторное произведение равно 0, т.е. . Это ещё одно ус- ловие коллинеарности векторов. (если векторы колли –неарны, т.е. параллельны, то и, по условию 1) определения, вектор имеет нулевую длину).

В частности, для любого вектора.

4. (Постоянный множитель можно выносить за скобку).

5. . (Можно раскрывать скобки.)

Рассмотрим пример: найти площадь параллелограмма, по -строенного на векторах , которые заданы следующим образом: , если и угол между векторами равен .

По свойству 2, 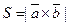. Найдём:

. Тогда

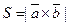
При решении примера мы использовали свойства вектор- ного произведения. По свойству 3, , по свой- ству 1, .

Пусть теперь векторы заданы своими координатами:

(7)

где базисные векторы имеют единичную длину, вза -имно перпендикулярны и образуют правую тройку. Тогда для них выполняются следующие правила векторного умножения:

 

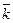
О

 

Найдём векторное произведение векторов и , используя эти правила, умножив векторы, заданные формулой (7), как скобку на скобку.

Но последнее выражение задаёт разложение по первой строке следующего определителя, т.е.

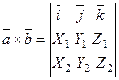. (8)

 

Пример. Найти площадь треугольника с вершинами (1, 1, 1),

(2, 3, 4) и (4, 3, 2) и его высоту, опущенную из вершины .

.

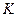
Найдём векторное произведение:

Тогда

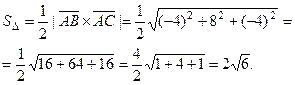
Высоту треугольника можем найти следующим образом:

 

3. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.

Для трёх векторов можно ввести смешанное произведение, при котором два вектора перемножаются векторно и получен- ный в результате вектор скалярно умножается на третий век- тор, в результате чего получается число.

Смешанное произведение векторов обозначается:

Любая циклическая перестановка не меняет смешанное произ- ведение: 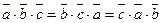. Остальные перестановки меняют знак произведения на противоположный.

 

ТЕОРЕМА. Смешанное произведение векторов равно

где - объём параллелепипеда, построенного на векторах .

В самом деле, рассмотрим рисунок

 

 

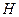
Тогда, если учесть, что - площадь параллело- грамма, построенного на векторах 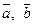, а 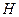- высота, построенного параллелепипеда, то

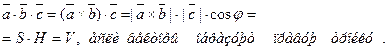
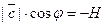Если векторы образуют левую тройку, то вектор направлен в противоположную сторону, угол тупой и , и . Если векторы компла -нарны, то и смешанное произведение равно 0.

Условие компланарности векторов:

(9)

Если векторы не компланарны, т.е. , то они образуют базис, т.е. любой вектор пространства можно представить в виде их линейной комбинации.

 

Если векторы заданы своими координатами: , то, как в случае скалярного и векторного произведения, можно показать, что:

. (10)

Учитывая теорему, можно найти объём параллелепипеда, построенного на векторах , по формуле:

,

а объём треугольной пирамиды, построенной на тех же векторах:

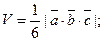(11)

высоту параллелепипеда или пирамиды можно найти по фор- муле:

. (12)

Рассмотрим примеры:

1. Найти объём треугольной пирамиды с вершинами

в точках

и найти её высоту, опущенную на грань .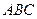

Найдём координаты трёх векторов, выходящих из одной точки, на которых строится пирамида: .

Тогда:

Таким образом, по формуле (11), объём пирамиды равен:

Чтобы найти высоту пирамиды, найдём векторное произве- дение:

Отсюда .

Тогда, по формуле (12)

2. Проверить, что точки

лежат в одной плоскости.

 

Если данные точки лежат в одной плоскости,

 

 

С

 

 

 

 

 

то векторы 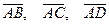компланарны. Найдём координаты этих векторов:

Векторы компланарны, если их смешанное произведение рав- но нулю, т.е. должно быть выполнено равенство:

.

Найдём это смешанное произведение по формуле (10):

Смешанное произведение равно нулю. Следовательно, точки лежат в одной плоскости.

3. Поверить, что векторы образуют базис и найти разложение вектора в этом базисе:

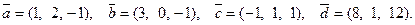
Если векторы образуют базис, то их смешанное произведе- ние . В нашем случае:

следовательно, векторы образуют базис

Тогда 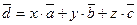представляет собой разложение вектора в этом базисе. Найдём коэффициенты этого разло- жжения, для чего запишем соответствующее векторное равен -ство:

.

Учитывая правила действий с векторами, получим систему:

Решим данную систему линейных уравнений методом Гаусса. Запишем расширенную матрицу системы и получим нули ниже главной диагонали.

 

 

Умножим первую строку на (-2) и прибавим к второй строке и просто прибавим её к третьей строке. Получим:

Умножим третью строку на (3) и прибавим к второй, после че- го разделим вторую строку на (3), а третью на (2) и поменя -ем их местами:

.

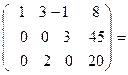
Получили систему:

Таким образом: Тогда

 

§ 4 ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА

 

Изучая геометрические векторы, мы установили взаимно од- нозначное соответствие между направленными отрезками и упо- рядоченными наборами чисел (координатами векторов). При этом сложение векторов и умножение их на число производит- ся покоординатно. Обобщим вышесказанное следующим обра – зом: упорядоченная совокупность 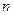чисел

называется 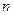- мерным вектором, а числа 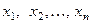- его координатами. Набор, состоящий из нулей, называется ну- левым вектором, т.е.