Пусть A =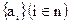 
- множество сравниваемых ПС, 
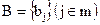- множество экспертов, участвующих в эксперименте; n 1 - число ПС, оцениваемых одним экспертом.
1. Эксперимент не сбалансирован.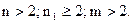 
Степень доминирования ПС a1 над aj по показателю Kr точно количественно установить невозможно.
Процедура сравнения 1. В этом случае по результатам экспертных оценок может быть построен ориентированный граф, отражающий взаимное доминирование ПС по заданному критерию Kr. Вершины графа отождествляются со сравниваемыми ПС. Если программное средство ai превосходит aj по качеству (признаку, критерию) Kr, то в матрице непосредственных путей графа на месте ij-го элемента ставится единица.
Матрица доминирования, построенная по соответствующему графу, является алгебраической формой записи отношения доминирования. Численно степень доминирования, т.е. степень превосходства (значимость) ПС ai по критерию Kr, определяется рангом, равным сумме элементов i-й строки матрицы S:
S = D + D2,
где D - матрица доминирования.
Если отказаться от требования доминирования, допустив наличие двухсторонних связей (эксперт не видит разницы между ПС ai и aj) и петель при вершинах, то ранг программного средства ai определится как сумма элементов i-й строки матрицы S1:
S1 = A + A2,
где A - матрица непосредственных путей исходного ориентированного графа.
Процесс построения матрицы непосредственных путей A сводится к следующему:
1) определяется порядок матрицы A по числу вершин в исходном графе (равен n - числу сравниваемых ПС); 2) вершины исходного графа (сравниваемые ПС) нумеруются в произвольном порядке; этими же номерами обозначаются строки и столбцы матрицы A; 3)если из вершины i графа к вершине j имеется один или несколько непосредственных путей, то элемент матрицы A на пересечении i-й строки и j-го столбца будет равен единице или некоторому натуральному числу, равному количеству непосредственных путей из вершины ai к вершине aj; в противном случае (если непосредственных путей нет) этот элемент будет равен нулю.
В практических расчетах, чтобы получить характеристику числовой меры ПС из качественного превосходства одного ПС над другим, достаточно возвести матрицу непосредственных путей орграфа в невысокую степень, например, четвертую, а затем суммы элементов строк полученной матрицы разделить на сумму всех элементов матрицы.
Пример расчета. Пусть при сравнительной экспертной оценке пяти ПС по одному из показателей, характеризующих качество эксплуатационной документации, получена нижеследующая матрица непосредственных путей А:
| е11 | |||||||||||||||
| , | 
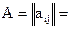
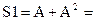
| е10 | ||||||||||||
| е8 | |||||||||||||||
| е10 | |||||||||||||||
| е8 |
2. n > 2; n1 = 2; m = n(n-1)/2. Степень доминирования ПС ai над aj по показателю Kr можно характеризовать числом.
Процедура сравнения 2. Если по некоторому показателю (критерию) каждой паре программных продуктов ai - aj некоторой группы A,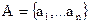 
экспертами может быть дана количественная оценка Sij > 0, означающая превосходство ai над aj соответственно в Sij раз, то совокупность элементов 
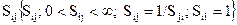образует матрицу превосходства 
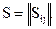Относительные веса (значимость) объектов группы A отождествляются (см. [5]) с компонентами собственного вектора 
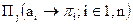матрицы S.
Поскольку собственные векторы определяются с точностью до произвольного множителя, то компоненты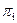 
вектора Пj целесообразно нормировать так, чтобы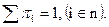 
Если оценка ПС проводится по совокупности показателей, например, по надежности, удобству сопровождения и т.д., то после экспертной количественной оценки парных предпочтений по каждому показателю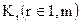 
отдельно для каждой пары вершин ai-aj мультиграфа превосходства, соответствующего группе ПС, получаем mдуг ((ij); (ji)) с оценками 
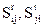. Запись 
означает, что ПС aj превосходит ПС ai по показателю Kr в q раз, при этом 
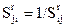, а веса показателей заданы, т.е.
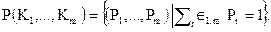
Пример расчета. Пусть сравнивается группа ПС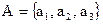 
по критерию удобства сопровождения. Экспертная оценка дала следующие результаты: S12 = 2,5; S13 = 5; S23 = 0,125.
Матрица превосходства для рассматриваемых ПС имеет вид:
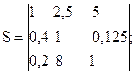
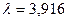
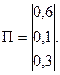
Пусть далее для той же группы объектов парные предпочтения оценивались по совокупности критериев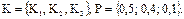 
| 
| 
| ||
| 
| 
| ||
| 
| 
|
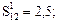
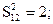
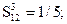
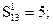
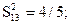
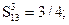
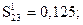
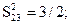
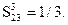
Вычислим элементы Sij матрицы превосходства.
| 
| |
| 
| |
| 
|
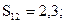
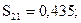
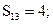
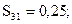
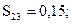
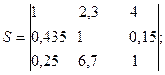
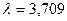
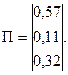
Замечание. При использовании рассмотренных процедур следует учитывать, что ранг (вес, значимость) объекта - это относительный показатель, и ранг отдельного программного средства должен сопоставляться с рангами всех n участвующих в эксперименте ПС.
3. n = n1 = 2; m > n. Сравниваемые ПС по каждому выбранному показателю оцениваются экспертами определенным числом баллов.
Процедура сравнения 3.1. Результаты эксперимента могут быть представлены двумя связанными рядами оценок (табл.1):
Таблица 1
План эксперимента (для условий 3)
| Эксперимент | Результаты эксперимента | |
| ПС а1 | ПС а2 | |
| a1 | b1 | |
| a2 | b2 | |
| … | … | |
| i | ai | bi |
| … | … | |
| m | am | bm |
Случай 1. Распределение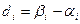 
подчиняется нормальному закону. Проверку значимости различия между двумя ПС по заданному показателю можно осуществить с использованием t - критерия с (m - 1) степенями свободы.
Нуль-гипотеза: математическое ожидание разности d равно нулю (сравниваемые ПС равноценны).
Случай 2. Если нет уверенности в том, что распределение d является нормальным для проверки значимости различия между ПС можно использовать ранговый критерий УИЛКОКСОНА.
Напомним, что нулевые значения di исключаются из рассмотрения и при расчетах число наблюдений n сокращается соответственно до числа ненулевых значений di (до mr). Абсолютное значение | di | упорядочивают по рангам Ri. Если среди ненулевых значений | di | есть равные, то им приписывается средний ранг. Вычисляются суммы положительных SRi(+) и отрицательных SRi(-) рангов, и меньшая из сумм используются в качестве статистики.
При mr > 25 можно воспользоваться аппроксимацией нормальным распределением.
Замечание. Преимущества описанной процедуры заключаются в том, что при обработке парных наблюдений по сравнению со стандартными методами сравнения средних значений независимых выборок уменьшается рассеяние внутри выборок. Кроме того, распределение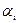 
и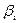 
может значительно отличаться от нормального, в то время как распределение 
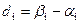будет достаточно хорошо аппроксимироваться нормальным распределением.
Процедура сравнения 3.2. Гораздо меньший объем вычислений потребуется для проверки значимости различия между системами, если воспользоваться критерием знаков Диксона и Муда. Здесь постулируется лишь независимость результатов измерений изучаемой переменной у отдельных систем.
Нуль-гипотеза: разности результатов оценки обеих систем (разности парных сравнений) в среднем (статистически) не отличаются от нуля, а значение медианы распределения разности равно нулю, т.е. число положительных и число отрицательных разностей должны быть равными. Нулевые разности исключаются из рассмотрения. Вероятность определенного числа плюсов и минусов определяется на основе биноминального распределения при ð=q=0.5. При mr >50 биноминальные значения могут быть аппроксимированы с помощью критерия c2, вычисляемого по формуле:
c2 =((|fo(+)-fe|-0.5)2+(|fo(-)-fe|-0.5)2)/fe,
где fo(+), fo(-) - соответственно фактические (полученные в эксперименте) частоты знаков «плюс» и «минус», fe - ожидаемая частота, равная 0,5*mr.
Если расчетное значение c2 меньше табличного значения, то нулевая гипотеза принимается.
Следует, однако, учитывать, что с ростом объема выборки эффективность критерия уменьшается. Поэтому при больших mr для оценки вероятности определенного числа знаков можно использовать нормальное распределение, рассчитывая его параметр по формуле:
Z=(|2x-mr|-1)/ Ö mr,
где x - наблюдаемая частота более редких знаков, mr - число полученных в результате экспертизы значений di, iÎmr (экспертных оценок), уменьшенное на число нулевых разностей.
Процедура сравнения 3.3. В качестве быстрого критерия можно воспользоваться модификацией критерия знаков, в которой статистикой служит величина Т=|(число плюсов)-(число минусов)|.
Если T>2Ö mr, то на 5% уровне при двустороннем критерии разница должна рассматриваться как значимая.
Пример расчета. При сравнении двух программных систем были опрошены специалисты отделов компьютеризации ряда коммерческих и финансовых организаций. Экспертам предлагалось на основании рекламных проспектов оценить каждую из сравниваемых систем по 100 балльной шкале. Чтобы элиминировать (или уменьшить) влияние субъективных факторов и повысить заинтересованность участников в результатах экспертизы, каждой организации была обещана помощь в освоении и внедрении лучшей системы.
Результаты эксперимента представлены в нижеследующей таблице.
| Номер эксперимента | ПП1 | ПП2 | di ПП1-ПП2 |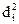 
|
| -3 | ||||
| -12 | ||||
| -15 | ||||
| +10 | ||||
| -5 | ||||
| +15 | ||||
| -10 | ||||
| +8 | ||||
| -9 | ||||
| -21 |
Как уже отмечалось, при обработке парных наблюдений уменьшается рассеяние внутри выборок и распределение разности значений оценок d i приближается к нормальному распределению. Поэтому при проверке значимости различия средних значений воспользуемся t-критерием, вычисляемым по формуле:
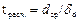с числом степеней свободы (m-1),
где dср,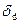 
- соответственно среднее значение и среднее квадратическое отклонение.
Статистический критерий: t -критерий, двусторонний. Уровень значимости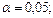 
tтабл.= 2,3; tрасч.= 0,8 <tтабл .
Таким образом, потенциальные пользователи не могут отдать предпочтение какой-либо из систем. Проверка значимости различия по непараметрическому критерию Уилкоксона для разностей пар дала такие же результаты.
4. n = n1 = 2; m > n. Сравниваемые ПС оцениваются экспертами по альтернативному признаку (зависимая выборка).
Процедура сравнения 4.1 При заданных условиях результаты эксперимента целесообразно представить в виде таблицы сопряженности признаков (табл.2) и использовать для определения значимости различия между программными системами методы статистического анализа категоризованных переменных.
Таблица 2
План эксперимента (для условий 4)
| |||
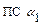
| I (превосходит по i-му показателю) | I (не I) | ||
| I | a | b |
| I (не I) | n | d |
Пример. Пусть оценивается качество n1(n1=2) программных продуктов a1 и a2 двумя группами специалистов. Причем первую группу (из m1 специалистов) составляют разработчики программных систем (a1), а вторую (из m2 специалистов) - программисты-пользователи (a2).
Нулевая гипотеза H0: доли специалистов из первой и второй групп, предпочитающих систему a1 (a2) совпадают. Альтернативная гипотеза H1: доли специалистов из каждой группы, отдающих предпочтение системе a1 (a2) в генеральной совокупности разные.
Результаты оценки представляются в таблице сопряженности признаков вида:
| а1 | а2 | Итого | |
| Г1 | А | В | A+B = m1 |
| Г2 | С | Д | C+Д = m2 |
| Итого: | А+С | В+Д | m |
Статистический критерий: если m =(m1 + m2) Ј 30 и при этом m1,m2 Ј 15, то можно использовать точный критерий Фишера. Если m > 30 и A –Д і 15, то целесообразно использовать приближенный критерий c2.
c2= ее(|F0 - FL| - 0,5) / FL. При c2 > c2 табл. принимается гипотеза H1 (суммирование производится по всем клеткам таблицы). Значения ожидаемой частоты FLI для каждой клетки вычисляется по формулам:
FLA = ((A+B)(A+C))/N;
FLB = ((A+B)(B+D))/N и т.д.
Если n1>2, то поправка на непрерывность не производится и c2 вычисляется по формуле:
c2= ее(F0 – FL)2 /FL.
Замечание. С целью элиминировать влияние на результаты экспертизы очередности, в которой программные системы предъявляются эксперту, целесообразно проводить попарные сравнения систем разными группами специалистов и представлять результаты оценки в виде нескольких таблиц сопряженности признаков с последующим статистическим анализом адекватности результатов сравнения.
Предположим, что в условиях предыдущего примера подгруппы Г11 и Г21 сравнивали системы в последовательности a1-a2, а подгруппы Г12 и Г22 - в последовательности a2-a1. Результаты экспертизы представлены в двух нижеследующих таблицах:
| а1 | а2 | Итого | |
| Г11 | 25(А) | 7(В) | A+B = m11 |
| Г21 | 12(С) | 36(Д) | C+Д = m21 |
| Итого: | А+С | В+Д | m1 |
| а1 | а2 | Итого | |
| Г12 | 6(А) | 2(В) | A+B = m12 |
| Г22 | 5(С) | 17(Д) | C+Д = m22 |
| Итого: | А+С | В+Д | m2 |
Спрашивается, совпадают ли результаты сравнения. Гипотеза Ho: результаты совпадают, ожидаются лишь различия, обусловленные случайной изменчивостью.
В описанной ситуации вполне допустимым является использование критерия c2. В соответствии с гипотезой Ho ожидаемые значения в клетках второй таблицы должны быть такими же, как в первой, т.е. ð11 =0.3125; ð12 =0.087; ð21 =0.15; ð22 =0.45.
Тогда ожидаемые частоты fe для второй таблицы будут соответственно равны:
fe11= 30*0.3125=9.375; fe12= 2.625; fe21= 4.5; fe22= 13.5.
Вычислив c2 по формуле
c2расч=S(½ fo-fe½-0.5)2/fe,
найдем, что c2расч<<c2табл, т.е. нет оснований отклонить гипотезу Ho.
Процедура сравнения 4.2. При сравнении сложных ПС по нескольким показателям, например, по таким показателям, как качество документации, интерфейс, удобство сопровождения, трудоемкость освоения и др. результаты экспертизы могут быть представлены в виде k*2- таблицы сопряженности признаков.
| Характеристика качества | Сравниваемые системы | |
| ПС1 | ПС2 | |
| Качество документации | a1 | b1 |
| Интерфейс | a2 | b2 |
| Удобство сопровождения | a3 | b3 |
| Трудоемкость освоения | a4 | b4 |
Здесь ai, bi - соответственно количество экспертов, отдавших предпочтение по i -му показателю системе ПС1 (ai) и системе ПС2 (bi).
Нуль-гипотеза: в структуре результатов экспертизы обеих систем нет статистически значимых различий, т.е. по совокупности рассматриваемых признаков (характеристик) качество ПС1 и ПС2 одинаково.
Для проверки нуль-гипотезы можно использовать c2 -критерий Брандта и Снедекора c (k-1) степенями свободы.
Пример. Пусть при сравнении ПС1 и ПС2 получены следующие результаты:
| Характеристика качества | Сравниваемые системы | |
| ПС1 | ПС2 | |
| Качество документации | 10 (a1) | 10 (b1) |
| Интерфейс | 15 (a2) | 10 (b2) |
| Удобство сопровождения | 9 (a3) | 12 (b3) |
| Трудоемкость освоения | 5 (a4) | 7 (b4) |
Спрашивается, являются ли оба столбца оценок статистически однородными. Сравнение выполнить со статистической достоверностью 99%.
Нуль гипотеза Ho: в структуре результатов экспертизы нет статистически значимых различий.
c2расч=[(Sai/(ai+bi))-a2/n]*n2/a*b= 2.01.
Здесь a=Sai, b=Sbi, n=(a+b).
Так как расчетное значение c2расч меньше, чем табличное c23;0.01, нет оснований отклонить Ho.
Замечание. Если мы представляем исходные данные в виде таблиц сопряженности признаков (номинальная шкала), то при оценке связи между переменными могут использоваться различные модели, включая логарифмически-линейную, и меры связи (сравнительное исследование некоторых из широко используемых мер связи проведено в [7]). Однако, как отмечается в [6, с.139]), "с точки зрения оценки статистической значимости связи между строками и столбцами традиционный и логлинейный подходы к таблицам сопряженности, с одной стороны, и дуальное шкалирование, с другой стороны, дают сравнительно близкие результаты".
5. n > 2; n1 і 2; m > n. ПС оцениваются экспертами определенным числом баллов, причем участие одного эксперта в сравнении более чем 2-3 ПС нежелательно или невозможно по условиям эксперимента.
Процедура сравнения 5. В описанных условиях, по-видимому, единственно возможным и при этом достаточно корректным способом сравнения и выбора ПС оказывается применение методов неполноблочного планирования экспериментов в активно-пассивной постановке [2,3]. В частности, для устранения влияния неоднородностей и сокращения затрат времени и средств на проведение эксперимента можно использовать BIB - схемы, квадраты Юдена, решетчатые планы.
Процедура сравнения может осуществляться в такой последовательности:
1. В зависимости от числа сравниваемых ПС-претендентов и возможной (исходя из реальных условий) величины n1 выбирается конкретный план эксперимента.
2. В соответствии с требованиями плана формируется множество M ={bj}(j О z) пользователей-экспертов, каждый из которых проработал с любой из n1 ПС не менее заданного срока. Множество M состоит из k групп экспертов
M = U Mt, (t О k), а Mt = U Mt(e), (e О s).
Если, например, n1 = 2, то и s = 2. Тогда окажется, что эксперты, составляющие множество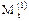 
, испытывали сравниваемые типы ПС (работали с ними) в последовательности 
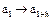, а множество 
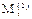- в последовательности 
.
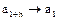Поясним содержание п.2 на примере. Предположим, что по выбранной характеристике или группе характеристик необходимо провести сравнение четырех ПС при условии, что каждый эксперт знаком только с двумя системами. При n = 4 и n1 = 2 целесообразно использовать BIB-схему с параметрами m = 18, 
= 3,k = 6. Здесь m -число экспертов; - число повторений каждой пары сравниваемых ПС; k=n(n - 1)/2 - число групп экспертов, каждый из которых оценивает одну пару ПС.
Тогда
Mt = Mt(1), U Mt(2); (t О g),
Mt(1), Mt(2) ={bj}, (j О d, d > l)
Условие d>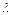 
желательно выполнять для того, чтобы облегчить выбор экспертов из d с учетом требований к структуре экспертной группы. Экспертам каждой группы присваиваются номера с использованием таблицы случайных чисел.
3. После того, как всем сравниваемым ПС экспертами, составляющими множество M, даны соответствующие оценки sij (для нашего примера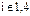 
), приступают к заполнению двух таблиц планирования эксперимента, причем первая из таблиц заполняется оценкамиsij, случайно выбранными из множеств 
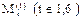, а вторая - оценками sij(1), из множеств Mt(2). Каждая из заполненных таким образом таблиц может обрабатываться раздельно. В дальнейшем результаты статистической обработки обеих таблиц сопоставляются и анализируются совместно. Возможно и объединение таблиц в одну с последующим статистическим анализом представленных в ней данных (тем самым элиминируется влияние на результаты сравнения "эффекта очередности").
Для экспериментальных данных, представленных в табл.3, в результате статистической обработки получены следующие значения F-критерия: F12=67,1; F13=18,0; F14=30,3; F23=15,6; F24=7,2; F34=1,6. Табличное значение для 1-процентного уровня значимости Fкртабл =8,68.
Таблица 3
