Студент должен:
иметь представление:
— о задачах корреляционно-регрессионного анализа;
— о парной регрессии на основе метода наименьших квадратов и метода группировок;
— о множительной (многофакторной) регрессии;
— о методах оценки существенной связи.
Корреляция. Парная, частная и множественная корреляция. Корреляционный анализ. Коэффициенты корреляции. Корреляционно-регрессионный анализ. Линейная и нелинейная регрессия. Прямая (положительная) и обратная (отрицательная) регрессия. Парная регрессия. Множественная (многофакторная) регрессия. Уравнение регрессии. Коэффициенты регрессии. Адекватность моделей, построенных на основе уравнения регрессии. Интерпретация моделей регрессии.
Методические рекомендации
Корреляция – это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
В статистике принято различать следующие варианты зависимостей: парная, частная и множественная корреляция.
С помощью корреляционного анализа определяется количественная теснота взаимосвязи и факторов, а с помощью регрессивного анализа определяется аналитическое выражение связи, в котором изменение одной величины, обусловлено влиянием одной или нескольких независимых величин. Изучая данную тему целесообразно придерживаться такой последовательности:
1) линейная регрессия;
2) криволинейная регрессия;
3) множественная регрессия;
4) определение оценок коэффициента корреляции и регрессивных уравнений.
Прежде чем приступить к корреляционно-регрессивному анализу необходимо качественно проанализировать изменения данного явления. Далее на конкретном примере рассмотрим применение статистического метода изучения взаимосвязи.
Пример. Определить коэффициент корреляции и построить уравнение регрессии по следующим данным. Исходные и расчетные данные о численности работающих и стоимости основных производственных средств даны в табл. 19:
Таблица 19
| Исходные данные | Расчетные данные | ||||
| Стоимость основных произ- водственных средств (млн.руб) | Численность работающих (тыс.чел) | х2 | ху | у2 | 
|
| х | у | ||||
| 12,0 10,1 8,2 7,2 7,2 6,3 4,8 3,4 2,4 2,4 | |||||
Решение. Можно считать, что зависимость здесь линейная и выражается формулой

где  - переменная, средняя (средняя численность работающих);
- переменная, средняя (средняя численность работающих);
х – стоимость основных производственных фондов;
а1 и а0 – параметры уравнения регрессии.
Параметры а1 и а0 найдем из системы нормальных уравнений:
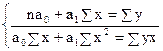
Далее подставим расчетные данные х2, у2 в систему уравнений и определим а1 и а0

Решив систему уравнений, получим параметры: а0 = 0,02 а1 = 0,48.
Уравнение регрессии будет иметь вид:

Далее определим коэффициент линейной корреляции по формуле:
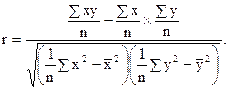
Подставляя расчетные данные, получим:

Положительный коэффициент корреляции говорит о наличии прямой зависимости между признаками, а его очень маленькое значение – в том, что между численностью и основными производственными фондами существует незначительная взаимосвязь, не тесная, т.к.
r – значительно меньше единицы.
[2, 7, 8].
Вопросы для самоконтроля
1. Что такое корреляция?
2. Какие вы знаете виды зависимости?
3. Чем отличается множественная корреляция от частной?
4. Можно ли изобразить корреляционную связь графически?
5. Назовите виды регрессий.






