Студент должен:
знать:
- понятие и классификацию индексов в статистике;
- значение индексного метода;
- способы исчисления индексов;
- взаимосвязи между индексами;
уметь:
- рассчитывать индивидуальные и общие индексы в статистике;
- осуществлять анализ структурных сдвигов на основе индексного метода;
- производить факторный анализ на основе индексного метода.
Индексы. Классификация индексов в статистике по степени охвата явления, базе сравнения, форме построения, объекту исследования, составу явления, периоду исчисления. Индивидуальные и общие индексы. Агрегатный индекс. Средние индексы. Индексы структурных сдвигов. Факторный анализ.
Методические рекомендации
Статистический индекс – это сложный относительный показатель, характеризующий среднее изменение массовых явлений, состоящих из непосредственно несоизмеримых элементов.
В статистике различают две группы индексов:
1) по характеру изучаемых объектов: индексы количественных показателей; индексы качественных показателей;
2) по степени охвата элементов совокупности: индивидуальные индексы; общие индексы.
где iр – индивидуальный индекс цен;
Р1 – цена единицы продукции в отчетном периоде;
Р0 – цена единицы продукции в базисном периоде.
где q1 – объем продукции отдельного вида в натуральном выражении за отчетный период;
q0 – объем продукции отдельного вида в натуральном выражении, в базисном периоде.
Индивидуальные индексы характеризуют изменение показателей по отдельному виду товара. Для характеристики изменения явления всей совокупности применяют общие индексы.
1. Агрегатный индекс цен с отчетными весами.
где 
- фактическая стоимость товаров (товарооборот) отчетного периода;
- условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.
2. Агрегатный индекс физического объема:
где 
- условная стоимость товаров, реализованных в отчетном периоде по базисным ценам;
- стоимость товаров, реализованных (произведенных) в базисном периоде по базисным ценам (базисный товарооборот).
3. Агрегатный индекс товарооборота:
(стоимости проданных товаров):
где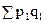 
- товарооборот отчетного периода,
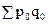- товарооборот базисного периода.
Между данными индексами существует взаимосвязь:
Jрq = Jp х Jq
В отдельных случаях невозможно применение агрегатных формул общих индексов. Например, в тех случаях, когда не известны отдельные значения р1 и q1, а известно их произведение р1q1 и индивидуальные индексы цен - 
В этих случаях необходимо преобразовать агрегатный индекс качественного показателя в средний гармонический или индекс количественного показателя в средний арифметический.
Например нам известно, что р1q1 и iр = р1/р0.
Для того, чтобы определить общий индекс цен, необходимо в агрегатную формулу общего индекса цен
подставить значение р0 =, тогда общий индекс цен будет вычисляться по формуле Jр = /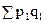 
(р1q1/ iр), это и будет формула среднего гармоничного индекса цен.
Приведем другой пример: известно, что р0q0 и 
необходимо вычислить общий индекс физического объема. В данном случае аналогично заменяем q1=q0 х iq и делаем подстановку в общий индекс физического объема:
- это формула среднего арифметического индекса физического объема.
Приведем примеры на расчет индексов.
Пример 1. Рассчитать индивидуальные и общие индексы товарооборота, физического объема проданных товаров и цен по следующим данным о ценах и реализации товаров за два месяца (табл.16).
Таблица 16
| Товары | Март | Апрель | Индексы | ||||||
| цена, руб. | реализация | цена, руб. | реализация | цена, руб. | физи- ческого объема продажи | товаро- оборота | |||
| кг | руб. | кг | руб. | ||||||
| А | 10,0 | 8,0 | 80,0 | 93,0 | 75,0 | ||||
| Б | 5,0 | 5,0 | 100,0 | 135,0 | 135,0 | ||||
| В | 6,0 | 7,0 | 116,7 | 133,0 | 155,6 | ||||
| Итого | - | - | - | - | 88,6 | 104,6 | 92,7 |
Индивидуальные индексы, характеризующие динамику показателей по каждому товару вычислены по формулам:
Например:
Индивидуальный индекс цен на товар А:
iр = 8,0: 10,0 =0,800 или 80,0% и т.д.
Индивидуальный индекс физического объема продаж по товару Б:
iq =540: 400 = 1,350 или 135,0% и т.д.
Индивидуальный индекс товарооборота товар В:
iрq = 1400: 900 = 1,556 или 155,6%
Все индивидуальные индексы помещены в последних трех колонках табл.16
Сводные индексы записаны по итоговой строке этих колонок. Они рассчитаны следующим образом.
Индекс цен:
11400/10900 х 100% = 104,6%
Фактический объем продажи возрос на 4,6% в апреле по сравнению с мартом.
Индекс товарооборота (стоимости проданных товаров) может быть получен по формуле:
930/1030 х 100% = 90,3%
Таким образом, стоимость проданных товаров в апреле месяце снизилась на 7,3% по сравнению с мартом. Между вычисленными общими индексами существует взаимосвязь: Jрq = Jp х Jq;
Проверим правильность вычислений: Jрq = 0,886 х 1,046 = 0,927 или 92,7%.
Пример 2. Рассчитать сводный индекс цен на основе следующих данных (табл.17):
| Товары | Изменение цен в % | Товарооборот отчетного периода (тыс.руб.) |
| А | +3 | |
| Б | -3 | |
| В | без изменений | |
| Итого | - |
Общий индекс цен будем определять по формуле средней гармонической
Следователь, в среднем на все три вида продукции цены повысились на 1,21%.
[3, 5, 7, 6, 8].
Вопросы для самоконтроля
1. Что такое индекс в статистике?
2. Какие задачи решают с помощью индексов?
3. Что характеризуют индивидуальные индексы?
4. В чем сущность общих индексов?
5. Какие вы знаете виды индексов?
6. Как исчисляется агрегатный индекс физического объема продукции и что он характеризует?
7. Когда возникает необходимость преобразования агрегатного индекса в средний арифметический или средний гармонический? Покажите на примерах.
8. Когда возникает необходимость преобразования агрегатного индекса в средний арифметический или средний гармонический? Покажите на примерах.
9. В чем выражается взаимосвязь индексов цен, физического объема и товарооборота, как практически она используется?
10. Какая система взаимосвязанных индексов используется при анализе себестоимости, физического объема, и затрат в производстве?
