ОГЛАВЛЕНИЕ
| Введение | ||
| Глава 1. | Классическое и геометрическое определения вероятности | |
| Глава 2. | Условная вероятность. Теоремы умножения и сложения вероятностей | |
| Глава 3. | Формула полной вероятности и формула Байеса | |
| Глава 4. | Схема независимых испытаний Бернулли. Предельные теоремы в схеме Бернулли | |
| Глава 5. | Дискретные случайные величины и их характеристики | |
| Глава 6. | Непрерывные случайные величины и их характеристики | |
| Глава 7. | Элементы математической статистики | |
| Список литературы | ||
| Приложения |
Введение
Настоящее учебное пособие содержит задачи и краткие теоретические сведения по основным разделам теории вероятностей и математической статистики в объеме, необходимом для их решения. Выбор разделов был обусловлен спецификой преподавания данного предмета на факультете нано-и биомедицинских технологий, а именно тем, что учебным планом предусмотрено только 17 часов практических занятий. По этой причине возникла необходимость в компактном задачнике, содержащем все темы учебного плана. В связи с этими обстоятельствами пособие имеет структуру, соответствующую семинарам: выделены разделы для работы в аудитории и самостоятельной работы.
Как правило, задачи из раздела для самостоятельной работы идентичны задачам из раздела для работы на семинаре и направлены на закрепление полученных знаний. Однако каждый раздел содержит и более сложные задачи. Глава, посвященная математической статистике, построена по другому принципу и содержит варианты для самостоятельной работы в силу того, что вообще задачи по статистике требуют много вычислений и проводить их в аудитории нецелесообразно.
Сборник задач составлен в соответствии с изложением материала в [7] и [8].
Глава 1. Классическое и геометрическое определения вероятности
Будем говорить, что произведен стохастический эксперимент, если результат этого эксперимента нельзя указать заранее. При этом известно множество возможных результатов эксперимента и это множество не изменяется при повторных экспериментах. Кроме того, стохастический эксперимент допускает возможность многократного повторения.
Определение. Элементарным исходом эксперимента 
называется результат, которым завершился стохастический эксперимент.
Множество элементарных исходов эксперимента обозначается 
. Записывают 
.
Определение. Случайным событием 
называется любое подмножество множества элементарных исходов экперимента , т.е. 
, 
, где 
– некоторая перестановка индексов элементов множества .
Классическое определение вероятности
Пусть – конечное множество равновозможных исходов, а –некоторое событие. Тогда вероятность события вычисляется по формуле:
(1.1)
где 
– количество иcходов, благоприятствующих событию , а 
–общее количество исходов эксперимента.
Задача.
В урне находится 
белых и 
черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.
Решение.
Стохастический эксперимент состоит в извлечении одного шара из урны, следовательно, элементарный исход эксперимента можно определить как «извлечен один шар».
Для указания множества необходимо перечислить все мыслимые в данном эксперименте исходы. Для рассматриваемого эксперимента можно записать: 
. Тогда событие 
.
Таким образом, 
, 
, и вероятность события равна
.
Сведения из комбинаторики.
При нахождении вероятностей в схеме классического определения используются элементы комбинаторики. Приведем некоторые необходимые определения.
Пусть имеется конечное множество 
некоторых элементов.
Определение. Сочетанием из элементов множества 
по называется любое подмножество {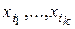 
} содержащее элементов, то есть сочетания представляют собой подмножества, различающиеся только составом элементов.
Число всех сочетаний 
(из элементов по ) вычисляется по формуле:
(1.2)
Пример. Пусть 
– множество букв латинского алфавита. Составим сочетания из 4 по 3. Получаем: 
.
Определение. Размещением из элементов множества по элементам (из элементов по ) называется любой упорядоченный набор (
) элементов множества Х.
Таким образом, размещения представляют собой такие подмножества, в которых различают не только состав, но и порядок следования элементов.
Число всех размещений 
(из элементов по ) определяется формулой:
. (1.3)
Пример. Пусть по-прежнему – множество букв латинского алфавита. Составим теперь размещения из 4 по 3. Получаем: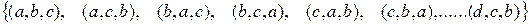 
. Всего 24 размещения.
Определение. Перестановкой из элементов по называется размещение 
(другими словами, элементов по местам).
Число всех перестановок 
вычисляется по формуле:
(1.4)
