Пусть дана система линейных алгебраических уравнений, матрица коэффициентов которой является квадратной и несобственной
.
Тогда, как известно из предыдущей лекции, решение системы дается матричной формулой
.
Будем для простоты рассматривать систему с тремя неизвестными. Тогда
.
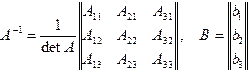Перемножая матрицы, получим
.
Обозначим главный определитель системы через 
. Так как по теореме Лапласа
,
,
.
Отсюда 
или 
.
Пример 6.1. Решить по правилу Крамера систему уравнений
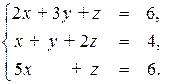
Вычислим главный определитель системы
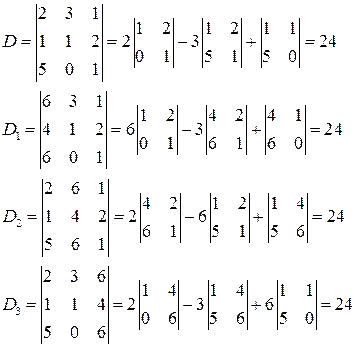
Отсюда получаем
.
Конец примера.
Вопрос 6.2. Метод Гаусса.
Метод Гаусса рассмотрим на примере решения системы уравнений
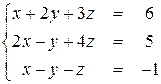
Выберем уравнение, которое содержит x. Такое уравнение будем называть ведущим. В качестве ведущего уравнения выберем первое. Используем ведущее уравнение для исключения x из второго и третьего уравнений. Для этого умножим ведущее уравнение на 2 и вычтем его из второго, затем вычтем его из третьего. Запишем ведущее уравнение первым, а результаты вычитания вторым и третим уравнением
Выберем теперь из второго и третьего уравнения новое ведущее уравнение, содержащее y. В качестве ведущего уравнения возьмем второе. Умножим его на 
и вычтем из третьего уравнения для исключения y. Тогда получим
В результате выполненных преобразований, которые называются прямым ходом, получаем систему уравнений с треугольной матрицей. Теперь выполним обратный ход. Из последнего уравнения системы найдем 
и подставим это значение во второе уравнение системы. Найдем величину y
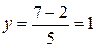
Из первого уравнения найдем теперь x
Таким образом, находим решение системы 
.
Отметим, что, выполняя прямой ход, мы использовали преобразования, которые не изменили определитель матрицы коэффициентов. Так как эта матрица после прямого хода стала треугольной, то величина определителя равна
.
Таким образом, метод Гаусса можно использовать для вычисления определителей. Наконец отметим, что метод Гаусса требует меньшее количество вычислений, чем правило Крамера.
Рассмотрим теперь систему уравнений
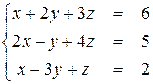
Выполняя первый шаг прямого хода метода Гаусса выберем первое уравнение ведущим и исключим с его помощью x
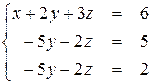
Исключая из третьего уравнения y, получим
Третье уравнение ни при каких значениях x, y и z не может быть выполнено. Поэтому эта система не имеет решений. Определитель исходной системы уравнений равен, как объяснено выше,
.
Можно доказать в общем виде, что у неоднородных систем уравнений с нулевым определителем нет решений, то есть такие системы уравнений несовместны.
Рассмотрим теперь систему уравнений
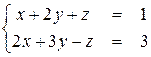
Исключая x из второго уравнения, получим
Эта система содержит три неизвестных и два уравнения. Перенесем слагаемые с z в правую часть
Переменные x и y называются базисными переменными, а переменная z ‑ свободной. Обозначим свободную переменную z через u. Тогда получим, решая систему, бесчисленное множество решений
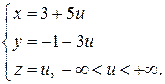
Таким образом, данная система уравнений неопределена.
Можно доказать, что любая система линейных уравнений имеет одно решение, или ни одного решения, или бесконечное множество решений. Система не может иметь конечное число решений большее одного.
Приведем в заключение следующую теорему:
Теорема 6.1. Всякая однородная система уравнений совместна и
1) при неравном нулю определителе определена;
2) при равном нулю определителе неопределенна.
