Определение 4.4. Минором элемента 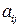 определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в котором находится данный элемент.
определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в котором находится данный элемент.
Обозначается минор элемента 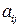 символом
символом 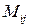 .
.
Пример 4.3. Минор элемента 

Определение 4.5. Алгебраическим дополнением элемента 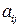 называется следующая величина
называется следующая величина
 .
.
Теорема Лапласа. Величина определителя равна сумме произведений элементов некоторой строки (столбца) на их алгебраические дополнения
 (разложение по i -й строке),
(разложение по i -й строке),
или
 (разложение по i -у столбцу),
(разложение по i -у столбцу),
где n - порядок определителя.
Сумма произведений элементов строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна 0.
Доказательство.
Пусть дан определитель 3-го порядка  .
.
Вычислим следующие определители по правилу Саррюса:



Но
 ,
, 

Поэтому  . Так как
. Так как 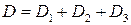 , то
, то

Аналогично доказывается разложение по любой другой строке или столбцу. Докажем теперь вторую часть теоремы. Пусть дана сумма произведений элементов второй строки на алгебраические дополнения элементов первой строки:

Согласно первой части доказательства, эта сумма равна определителю 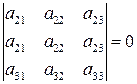 , равного 0 в силу равенства двух строк.
, равного 0 в силу равенства двух строк.
Конец доказательства.
Пример 4.4.

Конец примера.
Здесь  ‑ алгебраические дополнения, которые выражаются через миноры
‑ алгебраические дополнения, которые выражаются через миноры  порядка по формуле
порядка по формуле
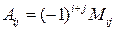 .
.
В свою очередь, минор  порядка является определителем
порядка является определителем  ‑ го порядка. Поэтому определитель n – го порядка определяется через определитель
‑ го порядка. Поэтому определитель n – го порядка определяется через определитель  порядка.
порядка.
Можно доказать, что свойства определителя, рассмотренные ранее, не зависят от порядка определителя.
Пример 5.1. Вычислить определитель
 .
.
Вычтем из второй строки первую, а из третей ‑ четвертую, получим определитель с двумя одинаковыми строками, следовательно, его величина равна 0.
Конец примера.
Вопрос 5.2. Обратная матрица.
Определение 5.1. Квадратная матрица B n ‑ го порядка называется обратной к квадратной матрице A, если
 .
.
Обратную матрицу будем обозначать символом  .
.
Теорема 5.1. Если матрица A имеет обратную матрицу, то
 .
.
Доказательство. Так как 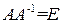 , то, вычисляя определитель, получим
, то, вычисляя определитель, получим

или

Конец доказательства.
Теорема 5.2. Если матрица A имеет отличный от нуля определитель, то она имеет обратную матрицу.
Доказательство. Приведем доказательство для матриц третьего порядка. Пусть матрица A

имеет отличный от нуля определитель. Рассмотрим матрицу B

Перемножим две матрицы
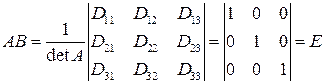
Здесь использованы обозначения (значения сумм вычислены по теореме Лапласа)

Аналогично доказывается, что  . Таким образом, матрица B является обратной для A.
. Таким образом, матрица B является обратной для A.
Конец доказательства.
Теорема 5.3. Если матрица имеет обратную, то обратная матрица единственна.
Доказательство. Пусть матрица A имеет две обратные матрицы B и C, тогда
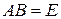 и
и  .
.
Умножим первое равенство на C слева

Конец доказательства.
Пример 5.2. Вычислить обратную матрицу

 , алгебраические дополнения
, алгебраические дополнения

Тогда получим обратную матрицу

Коней примера.






