Опредление 4.1. Матрицей размера  называется прямоугольная таблица чисел, состоящая из m строк и n столбцов
называется прямоугольная таблица чисел, состоящая из m строк и n столбцов
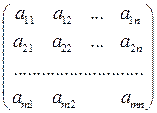
Числа, составляющие таблицу, называются элементами матрицы. Матрицы обозначаются большими латинскими буквами A, B, C..., а их элементы ‑ малыми латинскими буквами a, b, c....
Каждый элемент матрицы нумеруется двумя числами, которые называются индексами или указателями:
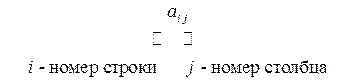
первый индекс указывает на номер строки, а второй ‑ на номер столбца. Если элементы матрицы состоят из вещественных или комплексных чисел, то матрица называется соответственно вещественной или комплексной.
Нулевая матрица ‑ матрица, состоящая из нулевых элементов, обозначается 0.
Квадратная матрица ‑ матрица размера 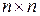 .
.
Треугольная матрица ‑ квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю.
Диагональная матрица ‑ квадратная матрица, у которой все элементы, расположенные вне главной диагонали равны нулю.
Единичная матрица ‑ диагональная матрица, диагональные элементы которой равны единице.
Над матрицами определены следующие действия: сложение, вычитание, умножение на число и на матрицу.
Опредление 4.2. Матрица C есть сумма матриц A и B, если все три матрицы одинакового размера и
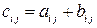
Тогда пишут  . Сложение матриц подчиняется двум законам
. Сложение матриц подчиняется двум законам
 ‑ коммутативный закон сложения,
‑ коммутативный закон сложения,
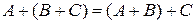 ‑ ассоциативный закон сложения.
‑ ассоциативный закон сложения.
Доказательство. Пусть  и
и  . Тогда
. Тогда  и
и
 .
.
Опредление 4.3. Матрица C есть разность матриц A и B, если все три матрицы одинакового размера и
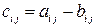
Тогда пишут 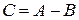 .
.
Опредление 4.4. Матрица C есть произведение числа a на матрицу A, если обе матрицы одинакового размера и

Тогда пишут  . Легко доказать следующие равенства
. Легко доказать следующие равенства
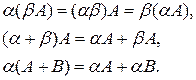
Доказательство.

Конец доказательства.
Пример 4.1. Вычислить матричное выражение 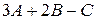 , где
, где
 .
.
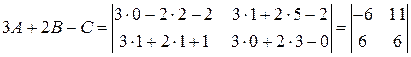
Конец примера.
Для дальнейшего изложения нам потребуется знак суммирования  для сокращенного обозначения суммы чисел
для сокращенного обозначения суммы чисел 
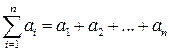 .
.
Докажем следующие свойства операции суммирования, основанные на переместительном, сочетаельном и распределительном законах сложения и умножения, то есть на возможности как угодно переставлять слагаемые и выносить общие множители за скобки:
1)  ,
,
2)  ,
,
3)  .
.
Доказательство.
1)

2)

3)
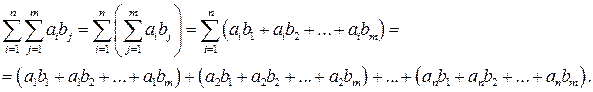
Сгрупперуем теперь слогаемые, собирая сначала члены, содержащие общие множители 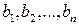

Опредление 4.5. Матрица C размером  называется произведением матриц A и B, если две последние имеют согласованные размеры
называется произведением матриц A и B, если две последние имеют согласованные размеры  и
и 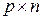 соответственно и
соответственно и
 (4.1)
(4.1)
Тогда пишут  . В формуле (4.1) используются элементы i строки матрицы A и элементы j столбца матрицы B, то есть строки первой матрицы "перемножаются" на столбцы второй матрицы. Из определения произведения матриц следует, что перемножать можно матрицы, у которых число столбцов первой матрицы равно числу строк второй матрицы.
. В формуле (4.1) используются элементы i строки матрицы A и элементы j столбца матрицы B, то есть строки первой матрицы "перемножаются" на столбцы второй матрицы. Из определения произведения матриц следует, что перемножать можно матрицы, у которых число столбцов первой матрицы равно числу строк второй матрицы.
Матричное умножение подчиняется следующим законам:
1) 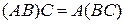 ‑ ассоциативный закон произведения,
‑ ассоциативный закон произведения,
2)  ‑ дистрибутивный закон умножения относительно сложения.
‑ дистрибутивный закон умножения относительно сложения.
Доказательство.
1) Пусть даны матрицы A, B и С соответственно размеров  ,
,  и
и  . Тогда
. Тогда
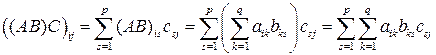 .
.
Поменяв местами порядок суммирования, получим
 ,
,
откуда следует равенство 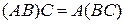 .
.
2) Пусть даны матрицы A, B и С соответственно размеров  ,
,  и
и 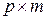 . Тогда
. Тогда
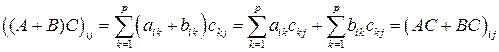 .
.
Конец доказательства.
Внимание! Матричное произведение не коммутативно, то есть матричные множители нельзя в общем случае менять местами.
Опредление 4.6. Квадратные матрицы 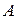 и
и  одинакового размера называются коммутирующими, если
одинакового размера называются коммутирующими, если  .
.
Опредление 4.7. Коммутатором квадратных матриц 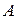 и
и  одинакового размера называется разность
одинакового размера называется разность  .
.
Очевидно, что если коммутатор  , то матрицы
, то матрицы 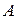 и
и  коммутируют и обратно, если матрицы
коммутируют и обратно, если матрицы 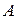 и
и  коммутирующиеся, то их коммутатор равен нулю
коммутирующиеся, то их коммутатор равен нулю  .
.
Пример 4.2. Вычислить произведения AB и BA, если
 и
и  .
.
 ,
,
 ,
,
 .
.
Конец примера.
Опредление 4.8. Транспонированием матрицы называется операция замены строк на столбцы. Будем обозначать символом  транспонированную матрицу A. Тогда элементы этих матриц связаны равенством
транспонированную матрицу A. Тогда элементы этих матриц связаны равенством
 .
.
Если матрица квадратная, то транспонирование сводится к вращению матрицы на 180 градусов относительно главной диагонали. Операция транспонирования обладает следующими свойствами

Доказательство.
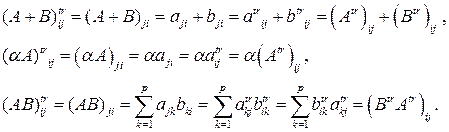
Конец доказательства.
Опредление 4.9. Матрица  называется сопряженной (реже эрмитово сопряженной) к матрице A, если она получена из матрицы A путем транспонирования и комплексного сопряжения ее элементов
называется сопряженной (реже эрмитово сопряженной) к матрице A, если она получена из матрицы A путем транспонирования и комплексного сопряжения ее элементов
 .
.
Операция сопряжения обладает следующими свойствами

Доказательство.

Конец доказательства.
Опредление 4.10. Квадратная вещественная матрица A называется симметричной, если она равна своей транспонированной  .
.
Из определения следует, что у симметричной матрицы элементы, расположенные симметрично относительно главной диагонали равны  .
.
Опредление 4.11. Квадратная комплексная матрица A называется самосопряженной (реже эрмитовой), если она равна своей сопряженной  .
.
Из определения следует, что у самосопряженной матрицы элементы, расположенные симметрично относительно главной диагонали комплексно сопряжены  , а элементы, стоящие на главной диагонали, вещественны
, а элементы, стоящие на главной диагонали, вещественны  .
.






